8.4 Проверка адекватности математических моделей

Симплекс-решетчатые планы насыщены. Поэтому для проверки адекватности полиномиальной модели необходимо выбрать N ≥ 1 контрольных точек на симплексе, провести в них эксперименты и проанализировать разницу между экспериментальными значениями свойства y и вычисленными по модели .

Выбирают контрольные точки в области, которая интересует исследователя, либо точки, которые можно использовать для построения полинома более высокой степени.

Процедура проверки адекватности заключается в вычислении значения t-критерия Стьюдента и сравнении его с табличным значением t_{табл,, f}, где f = N  (r – 1) при одинаковом количестве параллельных опытов r во всех контрольных точках.

При этом условии дисперсия опытов определяется по формуле:

, (8.25)

где – дисперсия опытов в u–й контрольной точке;

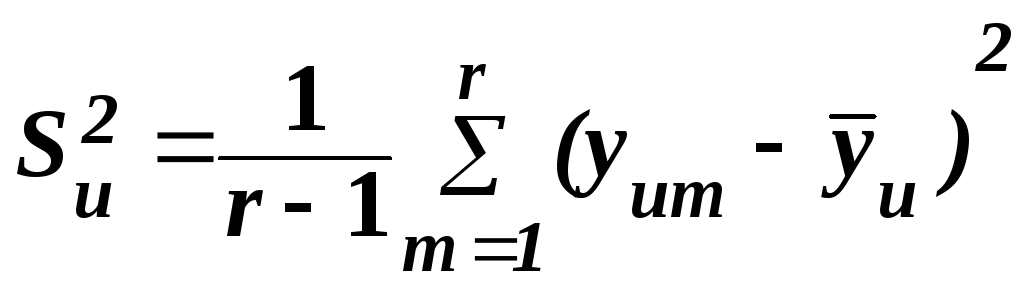, (8.26)

где y_um – экспериментальное значение свойства в m-м из r параллельных опытов в u-й контрольной точке;

– среднее значение свойства из r опытов в u-й контрольной точке.

Значение t_расч. вычисляется по формуле:

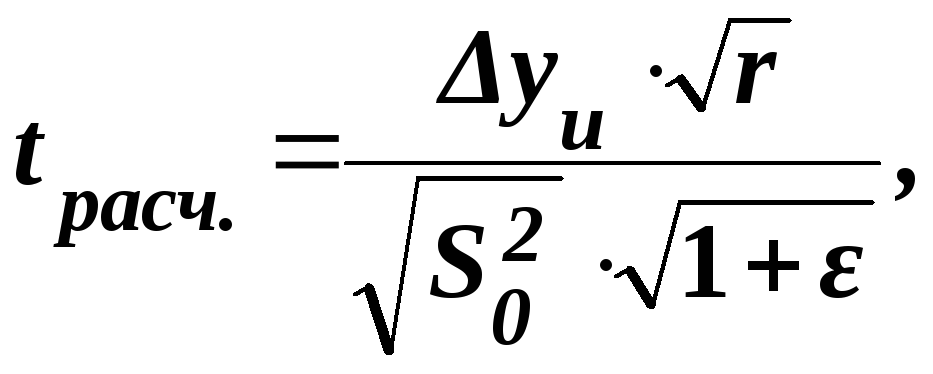(8.27)

где , – вычисленное по модели значение свойства, в u-й контрольной точке; ε – параметр, который зависит от состава смеси.

Если выполняется условие ≤ t_{табл,, f}, то гипотеза об адекватности модели принимается.

Выполнение этого условия необходимо для всех контрольных точек. В противном случае эксперимент дополняют новыми точками и переходят к полиному более высокой степени.

Значение параметра ε вычисляется по разным формулам – в зависимости от вида модели.

Для модели первой степени:

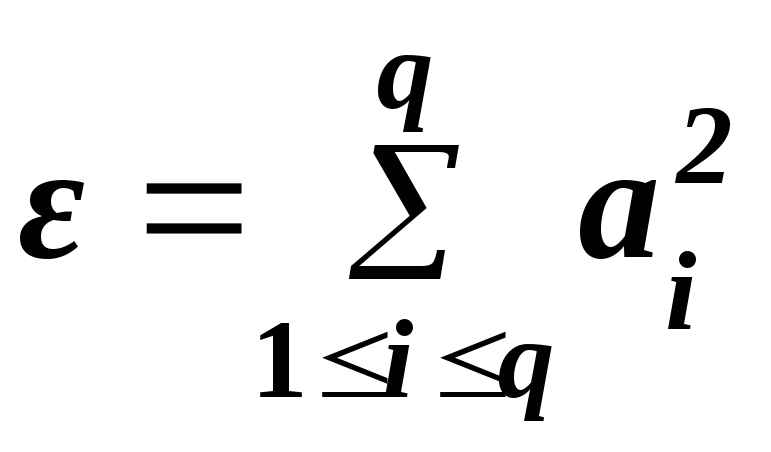, a_i = x_i. (8.28)

Для модели второй степени:

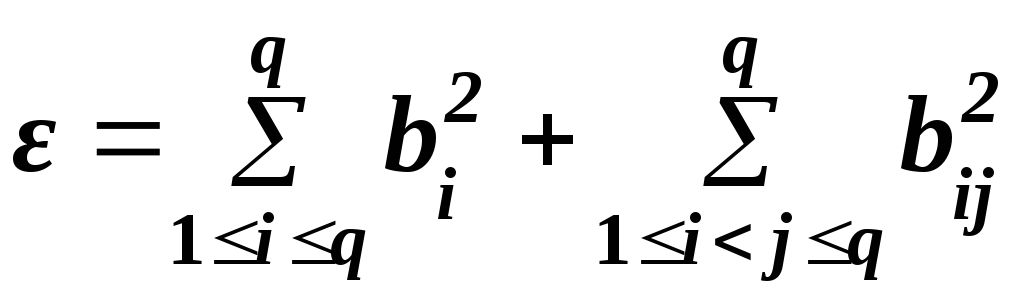, (8.29)

b_i = x_i(2x_i – 1) (8.30)

b_ij = 4x_ix_j. (8.31)

Для неполной кубической модели:

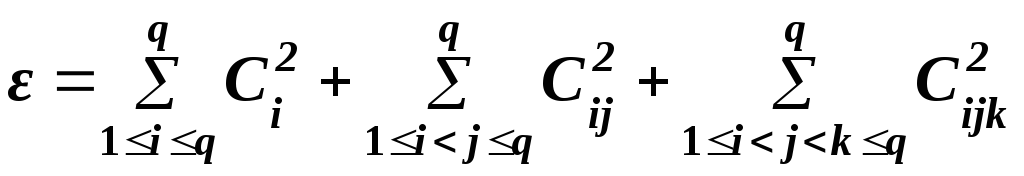, (8.32)

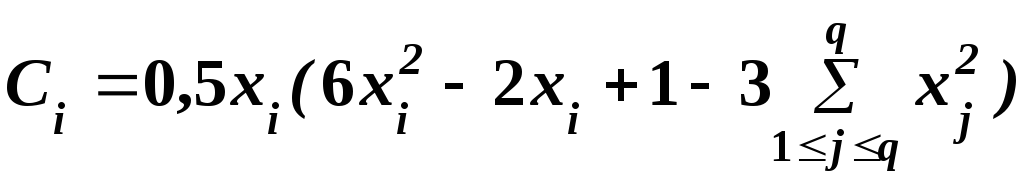; (8.33)

С_ij = 4x_i x_j (3x_i + 3x_j – 2); (8.34)

C_ijk = 27x_i x_j x_k. (8.35)

Проверка адекватности модели может также осуществляться по критерию Фишера, однако вышеописанный метод проверки признается более точным.

8.5 Планирование эксперимента при исследовании свойств многокомпонентных систем в ограниченной области изменения концентраций компонентов

На практике часто встречаются задачи по исследованию свойств многокомпонентной системы не по всей области концентраций компонентов 0  x_i  1, а лишь в ограниченной, которая может принимать разные формы, в том числе форму неправильного симплекса со сторонами разной длины. Состав систем, образующих вершины такого симплекса, как правило, известен. Можно принять эти системы за самостоятельные псевдокомпоненты и вводить для синтеза моделей все вышеназванные планы экспериментов. Планирование экспериментов осуществляется в системе координат псевдокомпонентов.

Пример. Известно, что никель-титановые и титано-алюминиевые плазменные покрытия обладают высокой жаростойкостью, коррозионной и кавитационной стойкостью. Необходимо установить оптимальные составы композиций тройных покрытий в части системы Ti(Х₁) – Ni(Х₂) – Al(Х₃), которая имеет форму неправильного симплекса Н – К – М (рис. 8.4).

Координаты вершин симплекса Н, К и М были приняты за псевдокомпоненты Z₁, Z₂ и Z₃. Они содержат соответственно (в долях единиц):

0,2Ti; 0,2Ni; 0,6Al;

0,2Ti; 0,7Ni; 0,1Al;

0,53Ti; 0,2Ni; 0,27Al.

Было принято решение синтезировать неполную кубическую модель. План эксперимента для построения такой модели, а также состав покрытий в трёх точках симплекса, выбранных для проверки адекватности модели, приведены в таблице 8.5 и на рисунке 8.4 (точки 8, 9, 10).

Оценивали скорость эрозии (мг/ч) стали 45 с плазменным порошковым покрытием. Каждый опыт повторяли трижды. Вместе с матрицей планирования, где псевдокомпоненты Z₁ представлены в долях единицы, таблица 8.5 содержит также истинный состав исходных компонентов х_і в экспериментальных точках.

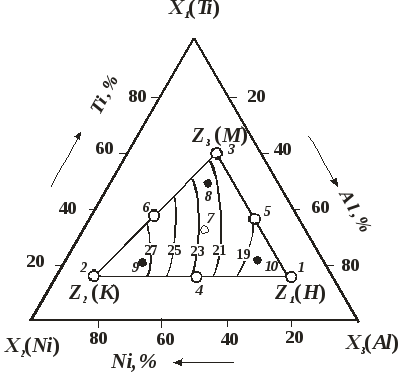
Рис. 8.4 План эксперимента и изолинии скорости эрозии стали 45 с разным составом плазменного покрытия из смеси порошков Ti, Nі и Al.

Таблица 8.5