5 Минор

Пусть  — квадратная матрица порядка  с коэффициентами из кольца ,.

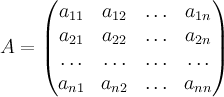Определение 1. Минором¹⁾ порядка  произвольной матрицы  называется определитель ее подматрицы порядка .

Таким образом, чтобы найти некоторый минор порядка , мы должны выполнить следующие действия. Зафиксируем в матрице  любые  строк с номерами  и  столбцов с номерами . Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу. Ее определитель 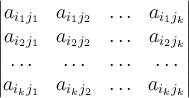 — это минор порядка , который мы будем обозначать через .

Пример 1. Рассмотрим матрицу порядка 3: 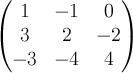. Выберем в ней 2-ю строчку и 3-й столбец. Тогда число, стоящее на пересечении этой строчки и этого столбца,  — минор порядка 1. Всего в этой матрице 9 миноров порядка 1.

Пример 2. В матрице из примера 3 выберем 1-ю и 3-ю строки и 1-й и 2-й столбец. Соответствующий минор  будет равен .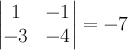

Определение 2. Пусть  — минор порядка  квадратной матрицы , построенный на строках с номерами  и столбцах с номерами . Вычеркнув из матрицы эти строки и столбцы, получим квадратную матрицу, определитель которой  будем называть дополнительным минором²⁾ к минору . Произвольный элемент  матрицы  можно рассматривать как минор . В этом случае  называют дополнительным минором к элементу .

Пример 3. Дополнительный минор к минору  из примера 4 равен .

Пример 4. Дополнительный минор к элементу  матрицы  из примера 3 равен .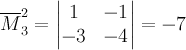

Алгебраическое дополнение

Определение 3. Пусть  — минор порядка  матрицы , построенный на строках с номерами  и столбцах с номерами . Величину будем называть алгебраическим дополнением³⁾ минора .

Пример 5. Алгебраическое дополнение минора  из примера 4 равно . Алгебраическое дополнение элемента  из примера 3 равно .

Теорема Лапласа

Теорема 1. (Теорема Лапласа) Зафиксируем в квадратной матрице  произвольные  строк с номерами . Тогда определитель матрицы  равен сумме произведений всевозможных миноров, построенных на этих строках, на их алгебраическое дополнение. То есть .

Если зафиксировать в матрице только одну строку с номером , то, как частный случай из теоремы Лапласа, получим следующую формулу: .

Пример 6. Вычислим определитель матрицы  из примера 3 с помощью разложения по первой строке: .

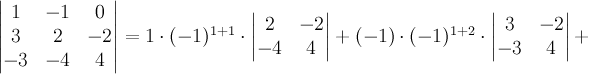
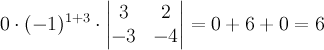6 Ранг матрицы

Количество линейно независимых строк матрицы называют строчным рангом матрицы, а количество линейно независимых столбцов матрицы называют столбцовым рангом матрицы. В действительности, оба ранга совпадают. Их общее значение и называетсярангом матрицы.

Другой эквивалентный данному подход заключается в определении ранга матрицы, как максимального порядка отличного от нуля минора матрицы.

Элементарные преобразования матриц

Основная статья: Элементарные преобразования матрицы

Элементарными преобразованиями строк матрицы называются следующие преобразования:

1. Умножение строки на число отличное от нуля,

2. Прибавление одной строки, умноженной на число, к другой строке,

3. Перестановка местами двух строк.

Элементарные преобразование столбцов матрицы определяются аналогично. При элементарных преобразованиях ранг матрицы не меняется.

7 Теорема о ранге.

 

Определение 4.3. Базисным минором матрицы называется любой ее ненулевой минор, порядок которого равен рангу матрицы.

 

Определение 4.4. Строки (столбцы) матрицы называются линейно зависимыми, если существует их линейная комбинация, не все коэффициенты в которой равны 0, равная нулевой строке (столбцу).

В противном случае строки (столбцы) называются линейно независимыми.

 

Замечание. Можно доказать, что необходимым и достаточным условием линейной зависимости строк матрицы является то, что одна из них является линейной комбинацией остальных.

Теорема 4.1. Строки и столбцы матрицы, элементы которых входят в базисный минор, линейно независимы. Любая строка (столбец) матрицы является линейной комбинацией этих строк (столбцов).

 

Доказательство (для строк).

1. Если бы базисные строки были линейно зависимыми, то с помощью эквивалентных преобразований из них можно было бы получить нулевую строку, что противоречит условию, что базисный минор не равен 0.

2. Строка, входящая в базисный минор, является линейной комбинацией его строк, в которой коэффициент при данной строке равен 1, а остальные коэффициенты равны 0.

Докажем это свойство для строки, не входящей в базисный минор.

Добавим к базисному минору эту строку (пусть ее номер – k) и любой столбец матрицы (пусть его номер – j). Затем разложим полученный определитель, равный 0 (так как его порядок больше ранга матрицы) по j-му столбцу:

 Поскольку является базисным минором,  поэтому, разделив полученное равенство на , найдем, что

 для всех j=1,2,…,n, где . Следовательно, выбранная строка является линейной комбинацией базисных строк. Теорема доказана.

8 Теорема о базисном миноре.  Столбцы матрицы А, входящие в БМ, образуют линейно независимую систему. Любой столбец матрицы А линейно выражается через столбцы из БМ.

Доказательство. Предположим противное - система длинных столбцов линейно зависима  система коротких столбцов (входящих в длинные)  линейно зависима ( по свойству определителя

БМ = 0. Противоречие, т.к. БМ.

Без ограничения общности считаем, что базисный минор расположен в левом верхнем углу. Покажем, что i-ый столбец линейно выражается через столбцы из БМ. i > r (иначе он сам является столбцом из БМ). Рассмотрим минор порядка на один больше, он будет нулевой.

Фиксируем . Раскладываем определитель по j-ой строке:

так как минор порядка (r + 1) - нулевой (где M₀ - БМ . Выражаем a_j,i:  Получены коэффициенты A₁,...,A_r. Для любого k:  (так как k - любое)

Следствие. Если все столбцы матрицы А линейно выражаются через r столбцов , которые образуют линейно независимую систему, то r_A = r.

Доказательство. Столбцы входящие в максимальную линейно независимую систему (в кол-ве r_A штук) линейно выражаются через . столбцы  (в кол-ве r штук) линейно выражаются через максимальную линейно независимую систему в кол-ве .

9 Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение – на A₂₁ и 3-е – на A₃₁:

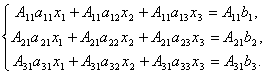
Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

.

Далее рассмотрим коэффициенты при x₂:

Аналогично можно показать, что и .

Наконец несложно заметить, что

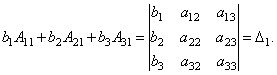
Таким образом, получаем равенство: .

Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Если имеем систему линейных уравнений, то таблица, составленная из коэффициентов при неизвестных, называется основной матрицей системы. Если к ней добавить столбец свободных членов - и получим РАСШИРЕННУЮ матрицу системы.