Тема 10. Статистический подход к распознаванию образов: использование метода группового учета аргументов (мгуа)

1. Постановка задачи аппроксимации функции по экспериментальным данным

Представим, что рассматривается некое множество объектов описываемых набором признаков X₁, X₂, … X_N, которое получено экспериментальным путем. Для любого объекта из данного множества в ходе эксперимента уже определен класс, к которому он принадлежит. Наша задача состоит в том, чтобы по данным нашей экспериментальной выборки построить такое «правило вынесения решения», которое позволило бы решать задачу определения принадлежности любого объекта рассматриваемого типа к определенному классу.

Иными словами, нам нужно определить некую процедуру в виде

Итак, у нас имеются экспериментальные данные в форме таблицы:

Y	X1	X2	…	XN
Y1	x11	x12	…	x1N
Y2	x21	x22	…	x2N
…	…	…	…	…
Ym	xm1	xm2	…	xmN

Каждый набор вида представляет собой вектор признаков определенного объекта данной экспериментальной выборки. Так же приводится класс, к которому он относится. Причем, тот или иной класс может быть представлен в данной экспериментальной выборке не одним вектором признаков.

Эти данные можно принять за таблицу значений функции Y = F(X₁, X₂, … X_N). Задача же заключается в том, чтобы при использовании этой таблицы экспериментальных данных попытаться найти такую функцию, которая могла бы с высокой точностью дать другие получаемые значения F при новых х₁, х₂, … х_N. Иначе говоря, функция, которая наиболее точно аппроксимирует функцию F(X₁, X₂, … X_N), представленную в выборке имеющихся экспериментальных данных.

С точки зрения распознавания образов мы имеем дело с задачей обучения РО с учителем. То есть нам предоставлена маркированная обучающая выборка, по которой необходимо получить распознающую процедуру (классификатор) f.

2. Метод наименьших квадратов для решения задачи аппроксимации функции по экспериментальным данным

Пусть функция задана таблицей своих значений: , .

			…
			…

Требуется найти многочлен фиксированной степени

,

для которого среднеквадратичное отклонение минимально.

Так как многочлен определяется своими коэффициентами, то фактически нужно подобрать набор коэффициентов , минимизирующий функцию .

Используя необходимое условие экстремума, , 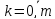получаем так называемую нормальную систему метода наименьших квадратов: , .

Полученная система есть система алгебраических уравнений относительно неизвестных . Определитель этой системы отличен от нуля, то есть решение существует и единственно. Однако при высоких степенях система является плохо обусловленной. Поэтому метод наименьших квадратов применяют для нахождения многочленов, степень которых не выше 5.

Пример 1.

Представим, что точки, относящиеся к разным классам, характеризуются двумя признаками и разделены между собой не явно, то есть их пересечение очень велико. Тогда функцию можно определить таким образом, что она остается почти одинаковой для всей совокупности объектов одного класса, т. е. для класса ; для класса . Функцию можно представить как поверхность в многомерном пространстве, построенную так, что изображениям разных классов соответствуют несвязанные отрезки на оси .

Рисунок 1. Обобщающие классифицирующие функции.

На рисунке 1 показано трехмерное пространство, двумя координатами которого являются элементы описания объекта и (признаки), а третьей — значение сложной функции 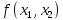. Нужно так построить разделяющую функцию , чтобы каждой точке плоскости, определяемой координатами и , соответствовали одинаковые значения , если каждая из рассматриваемых точек принадлежит одному и тому же классу. При этом класс может состоять из нескольких разобщенных областей, как это показано на рисунке 2. Очевидно, всегда можно построить такую поверхность, что независимо от характера распределения изображений проекции областей этой поверхности, соответствующих различным классам, на ось не будут иметь общих точек.

Согласно теореме Вейерштрасса, любую непрерывную на конечном интервале функцию можно со сколь угодно высокой точностью представить в виде полинома определенной степени. Таким образом, при любом распределении объектов в классах и при выборе аппроксимирующего нелинейного полинома в виде

(V.1)

всегда имеется возможность построить требуемую функцию . Здесь , , — признаки.

Решающее правило, основанное на построенной функции , в случае двух классов записывается так:

(V.2)

где и — средняя высота поверхности над изображениями первого и второго классов. Если же образов больше двух, то решающее правило принимает вид

. (V.3)

Задача обучения распознаванию образов была бы решена в приведенной постановке, если бы появилась возможность заранее определить необходимое для каждого конкретного случая число членов полинома (V.1) и после этого определить коэффициенты выбранного полинома. Если объект описывается признаками, то полином первой степени содержит членов, т. е. неизвестных коэффициентов; полином второй степени имеет членов, полином третьей степени — членов и т. д. Как видно, по мере усложнения полинома резко возрастает число его членов, а значит, и число коэффициентов, подлежащих определению.

Предположим, что сложность полинома уже определена. Как можно определить сами коэффициенты полинома? Для этого нужно каждому классу присвоить некоторое число. Тогда каждому объекту из обучающей последовательности будет соответствовать одна реализация уравнения (V.1), в левой части которого стоит число, соответствующее классу, а в правой — значения признаков. Для определения коэффициентов этих уравнений нужно составить и решить нормальные уравнения Гаусса. Если же для определения коэффициентов использовать адаптивные алгоритмы, включая и алгоритмы стохастической аппроксимации, то процесс Обучения может оказаться очень длительным. Кроме того, при этом задача выбора сложности полинома остается нерешенной.

Метод группового учета аргументов, во-первых, позволяет не заботиться о выборе сложности полинома (V.1), во-вторых, не предусматривает каких-либо заметных ограничений на число признаков (их может быть более ста), в-третьих, позволяет ограничить время определения коэффициентов практически допустимыми пределами, в-четвертых, может работать при обучающих выборках малого объема.