
- •Основы теории автоматического управления Конспект лекций
- •Терминология
- •Введение
- •1. Классификация систем автоматического регулирования
- •1.1. Классификация по основному признаку
- •1.2. Общая классификация систем автоматического управления
- •2. Математические модели элементов и систем управления
- •2.1. Передаточные функции. Преобразования Лапласа
- •2.2. Типовых звенья и их передаточные функции
- •2.2.1. Усилительное (безынерционное) звено
- •2.2.2. Интегрирующие звенья
- •1. Идеальное интегрирующее звено
- •2. Интегрирующее звено с замедлением
- •3. Изодромное звено
- •2.2.3. Дифференцирующие звенья
- •1. Идеальное дифференцирующее звено
- •2. Дифференцирующее звено с замедлением
- •2.2.4. Инерционное звено первого порядка (апериодическое)
- •2.2.5. Интегро-дифференцирующее звено
- •2.2.6. Инерционное звено второго порядка
- •2.2.7. Запаздывающее звено
- •2.2.8. Представление реальных аср типовыми звеньями
- •3. Основные характеристики звеньев и систем
- •3.1. Статические свойства элементов и систем
- •3.2. Соединения статических элементов
- •3.3. Временные характеристики
- •3.4. Частотные характеристики
- •3.5. Частотные характеристики типовых звеньев
- •1. Частотная характеристика усилительного звена (безынерционного)
- •2. Частотные характеристики инерционного звена первого порядка
- •3. Частотные характеристики интегрирующего звена
- •4. Дифференцирующее звено
- •5. Инерционное звено второго порядка
- •6. Колебательное звено
- •7. Запаздывающее звено
- •8. Частотные характеристики интегро-дифференцирующих звеньев и их соединений
- •3.6. Соединение звеньев. Передаточные функции соединений
- •1. Последовательное соединение звеньев
- •2. Параллельное соединение звеньев
- •3. Встречно-параллельное соединение звеньев или соединение с обратной связью
- •4. Эквивалентные преобразования структурных схем
- •3. Пропорцилнально-интегральные регуляторы
- •4. Пропорционально-интегрально-дифференциольные регуляторы
- •3.8. Последовательные и параллельные корректирующие устройства
- •3.9 Передаточные функции систем автоматического регулирования
- •4. Импульсные системы
- •4.1. Математическое описание дискретных объектов управления в электромеханических системах
- •4.2. Общие сведения об импульсных системах
- •4.3. Цифровые регуляторы в электромеханических системах
- •4.3.1. Методика синтеза регуляторов в мехатронной системе
- •5. Устойчивость линейных систем автоматического регулирования
- •5.1. Постановка задачи исследования устойчивости
- •5.2. Оценка устойчивости разомкнутой и замкнутой системы с помощью алгебраического критерия Рауса-Гурвица
- •5.3. Частотные критерии устойчивости
- •1. Критерий Михайлова
- •2. Критерий устойчивости Найквиста
- •Приложения
- •Список литературы
- •Оглавление
2. Математические модели элементов и систем управления
Математическое описание системы начинается с разделения ее на элементы, для которых должны быть составлены уравнения, описывающие их функционирование. Уравнения составляются на обнове анализа физических, химических, экономических и других процессов, происходящих в системе, с помощью законов сохранения энергии и вещества, законов электротехники, механики, гидравлики и т.д.
Система уравнений, с достаточной точностью описывающая поведение объекта во времени и пространстве, называется математической моделью. Разработка и уточнение моделей занимает от 80 до 90 процентов времени, затрачиваемого на проектирование систем автоматического управления [29]. При этом следует отдавать себе отчет, что никакая математическая модель физической системы не является точной. Можно повышать точность модели, увеличивая количество и сложность уравнений, но всё же не возможно добиться абсолютной точности. Поэтому следует стремиться к тому, чтобы модель адекватно отражала поведение физической системы в области её работоспособности и в то же время была не слишком сложной, доступной для аналитических преобразований и численного расчета.
2.1. Передаточные функции. Преобразования Лапласа
Исследование автоматической системы регулирования (АСР) существенно упрощается при использование прикладных математических методов операционного исчисления.
Дифференциальное уравнение (ДУ) элемента регулирующей системы связывает выходные величины с входными величинами и в общем случае имеет вид:
 (2.1)
(2.1)
где
![]() – выходная величина элемента (в
отклонениях от состояния
равновесия);
– выходная величина элемента (в
отклонениях от состояния
равновесия);
![]() – входная величина
элемента (в отклонениях от состояния
равновесия);
– входная величина
элемента (в отклонениях от состояния
равновесия);
![]() – постоянные
коэффициенты, определяемые конструктивными
особенностями и параметрами
настройки элемента.
– постоянные
коэффициенты, определяемые конструктивными
особенностями и параметрами
настройки элемента.
Если в уравнении
(2.1) вместо функций времени
![]() и
и
![]() ввести функции
ввести функции
![]() и
и
![]() комплексного переменного
комплексного переменного
![]() ,
поставив условием, что эти функции
связаны зависимостями
,
поставив условием, что эти функции
связаны зависимостями
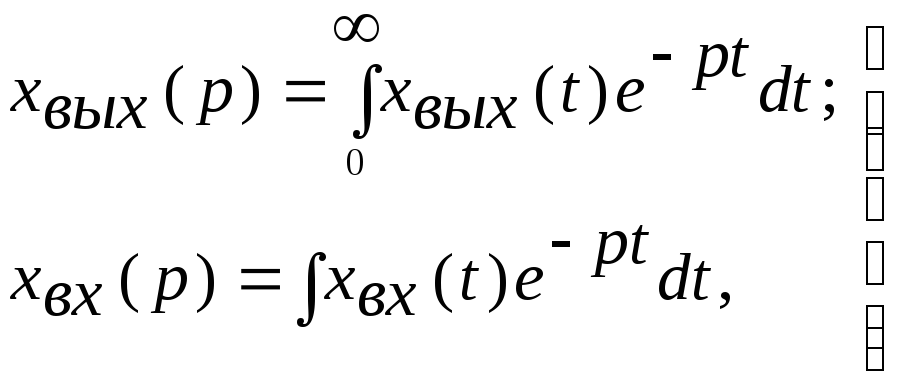 (2.2)
(2.2)
то оказывается,
что дифференциальное уравнение,
содержащее функции
![]() и
и
![]() при нулевых начальных условиях (при
при нулевых начальных условиях (при
![]()
![]() )
равносильно линейному алгебраическому
уравнению, содержащему функции
)
равносильно линейному алгебраическому
уравнению, содержащему функции
![]() и
и
![]() :
:
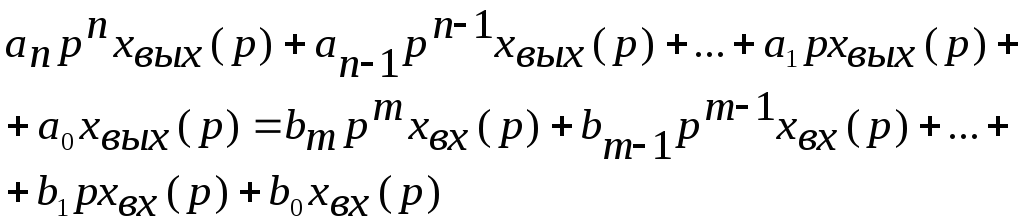 (2.3)
(2.3)
Такой переход от
дифференциального уравнения к однозначно
соответствующей алгебраической форме
называется преобразованием Лапласа.
Функция
![]() называется изображением функции
называется изображением функции
![]() ,
функция
,
функция
![]() называется оригиналом функции
называется оригиналом функции
![]() .
.
Операция перехода
от искомой функции
![]() к ее изображению
к ее изображению
![]() (нахождение изображение от оригинала)
называется прямым преобразованием
Лапласа, которое производится в
соответствии с преобразованием
Римана-Мелина:
(нахождение изображение от оригинала)
называется прямым преобразованием
Лапласа, которое производится в
соответствии с преобразованием
Римана-Мелина:
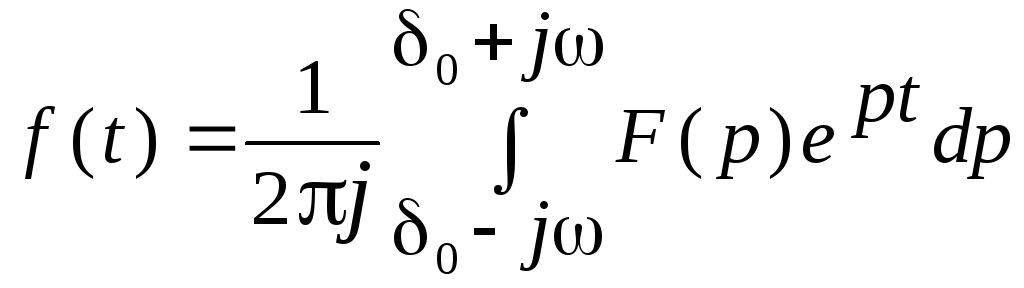 ,
,
в котором
интегрирование ведется в комплексной
плоскости вдоль бесконечной прямой,
параллельной мнимой оси и расположенной
правее всех особенностей функции
![]() .
Математически прямое преобразование
Лапласа записывается условно с помощью
символа
.
Математически прямое преобразование
Лапласа записывается условно с помощью
символа
![]() как
как
![]()
Операция перехода
от изображения
![]() к искомой функции
к искомой функции
![]() (нахождение оригинала от изображения)
называется обратным преобразованием
Лапласа. Математически обратное
преобразование Лапласа записывается
с помощью символа
(нахождение оригинала от изображения)
называется обратным преобразованием
Лапласа. Математически обратное
преобразование Лапласа записывается
с помощью символа
![]() как
как
![]()
Возможна запись соответствия между оригиналом и изображением по аналогии с таблицей
![]()
Практически
переход от дифференциального уравнения
к алгебраическому уравнению происходит
без каких-либо вычислений. Если сравнить
уравнение (2.1) с уравнением (2.3), то
нетрудно заметить, что формальный
переход от дифференциального уравнения
к алгебраическому при нулевых начальных
условиях получается путем замены
символов дифференцирования оригиналов
функций
![]() соответственно
соответственно
![]() и функций
и функций
![]() – их изображениями
– их изображениями
![]() .
С комплексной переменной
.
С комплексной переменной
![]() ,
как и с другими членами алгебраического
уравнения, можно производить различные
действия: умножение, деление, вынесение
за скобки и т.д.
,
как и с другими членами алгебраического
уравнения, можно производить различные
действия: умножение, деление, вынесение
за скобки и т.д.
Обозначив
производную
![]() ,
согласно (2.2) найдем изображение
,
согласно (2.2) найдем изображение
![]() .
.
![]() .
.
Интегрируя по частям, получим
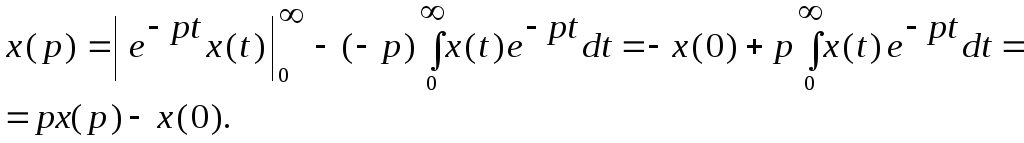
(так как![]() согласно условию существования интеграла
Лапласа).
согласно условию существования интеграла
Лапласа).
Итак, изображение производной при нулевых начальных условиях имеет вид:
![]()
Таким образом, мы
убедились в правомерности формального
перехода от дифференциальной формы
записи производной к ее записи в
операторной форме, заменив символ
дифференцирования
![]() комплексной переменной
комплексной переменной
![]() при нулевых начальных условиях.
при нулевых начальных условиях.
Так как
![]() ,
то
,
то
![]() и т.д.
и т.д.
Аналогично можно
доказать, что операции интегрирования
оригинала соответствует операция
деления изображения этого оригинала
на комплексный оператор
![]() .
Так при нулевых начальных условиях
.
Так при нулевых начальных условиях
![]() .
.
Поскольку интеграл суммы (разности) равен сумме (разности) интегралов от отдельных выражений, а постоянный множитель можно выносить за знак интеграла, то преобразование Лапласа обладает свойствами линейности, а именно
 ;
;
![]() .
.
Каждый элемент АСР в общем случае описывается дифференциальным уравнением вида (2.1). Следовательно, при выводе дифференциального уравнения системы в целом необходимо совместно решить несколько дифференциальных уравнений высших порядков.
Преобразование
дифференциальных уравнений по Лапласу
позволяет свести эту задачу к решению
системы алгебраических уравнений.
Определив из алгебраических уравнений
изображение
![]() искомой функции
искомой функции
![]() ,
определяющей переходный процесс в
системе, по таблицам соответствий
оригиналов и их изображений находят
эту функцию. (См. Приложение 1). Либо
вышеназванный переход можно осуществить
по известным формулам обратного
преобразования Лапласа в соответствии
с теоремой разложения.
,
определяющей переходный процесс в
системе, по таблицам соответствий
оригиналов и их изображений находят
эту функцию. (См. Приложение 1). Либо
вышеназванный переход можно осуществить
по известным формулам обратного
преобразования Лапласа в соответствии
с теоремой разложения.
Кроме того, преобразование уравнений по Лапласу дает возможность ввести очень значимое для теории управления понятие передаточной функции, характеризующей динамические свойства любого элемента системы. С помощью передаточных функций расчет систем автоматического регулирования (САР) еще больше упрощается и становится доступным широкому кругу инженерно-технических работников, не требуя применения сложного математического аппарата.
Вынося в уравнении
(2.3) за скобки
![]() и
и
![]() ,
получим:
,
получим:
![]() (2.4)
(2.4)
Определим из уравнения (2.4) отношение изображения выходной величины к изображению входной:
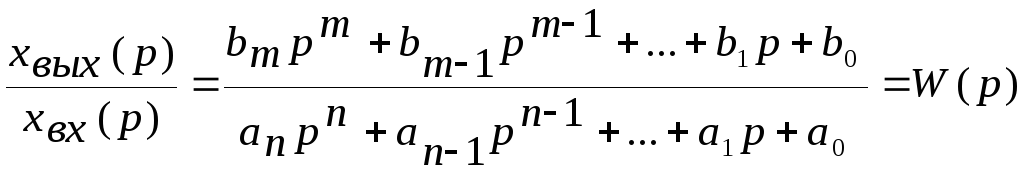 (2.5)
(2.5)
Отношение изображения выходной величины элемента системы к изображению его входной величины при нулевых начальных условиях называют передаточной функцией элемента системы.
Передаточная
функция
![]() является дробно-рациональной функцией
комплексной переменной
является дробно-рациональной функцией
комплексной переменной
![]() :
:
![]() , (2.6)
, (2.6)
где
![]() – полином степени
– полином степени
![]() ,
,
![]() – полином степени
– полином степени
![]() .
.
Из уравнения
(2.5) следует, что передаточная функция
элемента системы
![]() и изображение его входной величины
определяют изображение выходной
величины:
и изображение его входной величины
определяют изображение выходной
величины:
![]() . (2.7)
. (2.7)
Данное выражение есть реакция элемента системы на входное воздействие, эта реакция всецело зависит от передаточной функции, т.е. от динамических свойств элемент системы (звена). Предполагается, что входное воздействие известно – синусоидальное, единичное или импульсное.
