5. Устойчивость линейных систем автоматического регулирования

5.1. Постановка задачи исследования устойчивости

Понятие устойчивости, сформулированное для объектов управления и для отдельных звеньев, распространяется и на системы автоматического регулирования в целом. Устойчивость представляет способность системы автоматического регулирования возвращаться к исходному состоянию после кратковременного внешнего воздействия. Системы автоматического регулирования, как правило, должны быть устойчивыми.

Так же, как и в случае линейных звеньев, необходимым и достаточным условием устойчивости линейной системы автоматического регулирования является отрицательность вещественных частей всех корней ее характеристического уравнения. Вышесказанное может быть получено из передаточной функции замкнутой системы, связывающей любые ее вход и выход, путем приравнивания нулю знаменателя передаточной функции

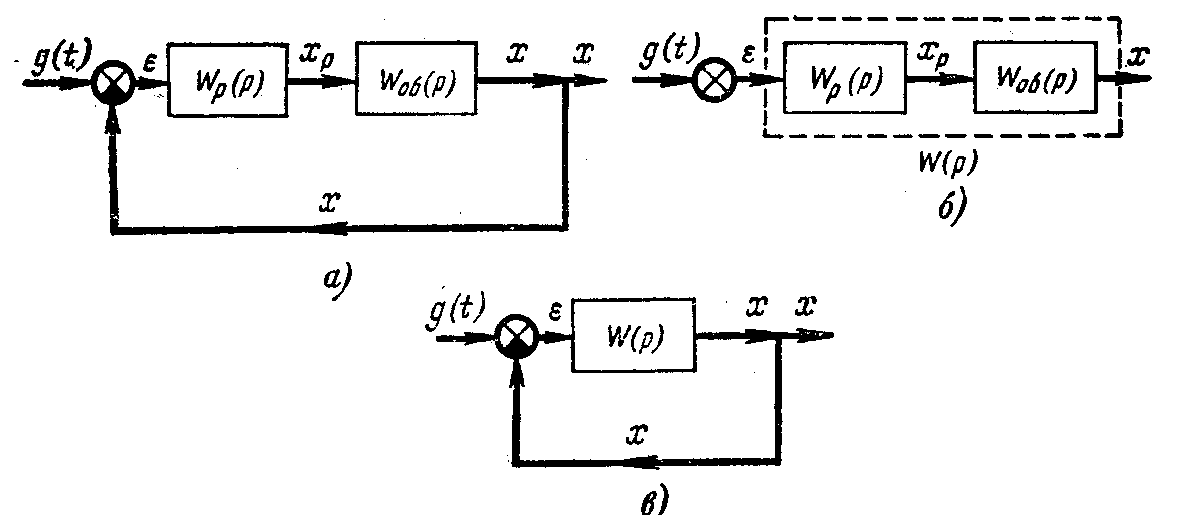
Рис. 5.1. Структурные схемы автоматического регулирования:

а, в – замкнутые системы; б – разомкнутая система

На рис. 5.1 показана структурная схема, к которой может быть приведена любая односвязная линейная схема автоматического регулирования при отсутствии всех внешних воздействий кроме задающего. Если передаточная функция разомкнутой системы

(5.1)

где K(p) и D(p) – полиномы степеней соответственно m и n , то передаточная функция замкнутой системы

, (5.2)

откуда путем приравнивания знаменателя нулю получается характеристическое уравнение замкнутой системы степени:

(5.3)

Обозначая

(5.4)

можно записать характеристическое уравнение в виде

(5.5)

5.2. Оценка устойчивости разомкнутой и замкнутой системы с помощью алгебраического критерия Рауса-Гурвица

Для характеристического уравнения (5.5) составим квадратную матрицу (таблицу коэффициентов), содержащую строк и столбцов:

(5.6)

Эта таблица составляется следующим образом.

По диагонали от левого верхнего до правого нижнего углов выписываются все коэффициенты по порядку от до . Каждая строка дополняется коэффициентами с нарастающими индексами слева направо так, чтобы чередовались строки с нечетными и четными индексами. В случае отсутствия данного коэффициента, а также, если индекс его меньше нуля или больше , на место его пишется нуль.

Критерий устойчивости сводится к тому, что при должны быть больше нуля все определителей Гурвица, получаемых из квадратной матрицы коэффициентов.

Определители Гурвица составляются по следующему правилу (см. (5.6):

; (5.7)

; (5.8)

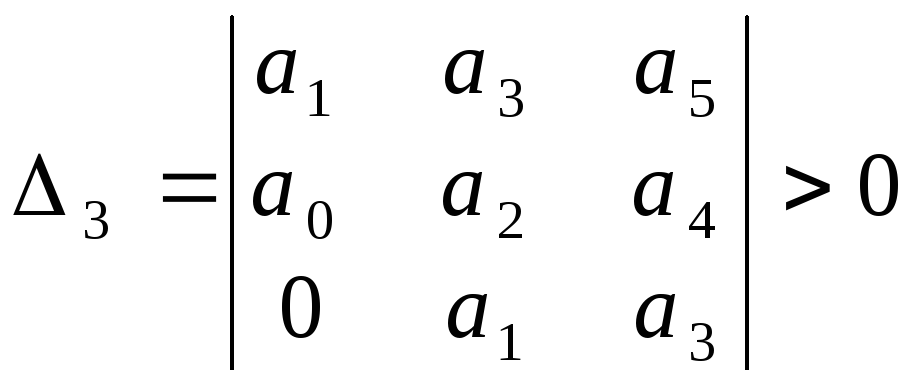; (5.9)

Последний определитель включает в себя всю матрицу. Но так как в последнем столбце матрицы все элементы, кроме нижнего, равны нулю, то определитель Гурвица выражается через последний член следующим образом:

. (5.10)

Однако в устойчивой системе предпоследний определитель тоже должен быть положительным. Поэтому условие положительности последнего определителя сводится к условию , т.е. к положительности свободного члена характеристического уравнения.

Условие нахождения системы на границе устойчивости можно получить, приравнивая нулю последний определитель: , при положительности всех остальных определителей. Как следует из (5.10) это условие распадается на два условия: и . Первое условие соответствует границе устойчивости первого типа (апериодическая граница устойчивости) и второе - границе устойчивости второго типа (колебательная граница устойчивости).

Для примера: Уравнение третьего порядка

.

Для этого уравнения получаем условия

; ; .

Третий (последний) определитель дает условие . Условие при , и может выполняться только при .

Следовательно, для уравнения третьего порядка уже недостаточно положительности всех коэффициентов характеристического уравнения. Требуется еще выполнение определенного соотношения между коэффициентами: .

Уже для уравнений пятой степени условия устойчивости по критерию Гурвица получаются достаточно громоздкими. Существенным недостатком является также то, что для уравнений высоких порядков в лучшем случае можно получить ответ о том, устойчива или неустойчива система автоматического управления. При этом в случае неустойчивости системы критерий не дает ответа на то, каким образом надо изменить параметры системы, чтобы сделать ее устойчивой. Это обстоятельство привело к поискам других критериев, которые были бы более удобными в инженерной практике.

Для иллюстрации применения критерия Гурвица рассмотрим пример на определение устойчивости дистанционной следящей системы. Принципиальная и структурная схемы изображены на рис. 5.2.

Рис. 5.2. Функциональная и структурная схемы следящей системы

В качестве чувствительного элемента использованы два сельсина (СД и СП), включенные по трансформаторной схеме. Передаточная функция сельсинов равна коэффициенту передачи схемы:

,

где – ошибка, равная разности углов поворота командной и исполнительной осей.

Передаточная функция усилителя:

,

где – коэффициент усиления и – постоянная времени усилителя.

Передаточная функция двигателя (Д):

,

где – коэффициент передачи двигателя по скорости, а – электромеханическая постоянная времени двигателя совместно с оконечным каскадом усилителя.

Передаточная функция редуктора (Р) равна его коэффициенту передачи, определяемому передаточным отношением:

.

Так как цепь управления состоит из включенных последовательно звеньев, то передаточная функция разомкнутой цепи будет равна произведению передаточных функций отдельных звеньев:

, (5.11)

где – общий коэффициент усиления разомкнутой цепи.

Характеристическое уравнение замкнутой цепи:

.

После подстановки получаем

. (5.12)

В данном случае характеристическое уравнение имеет третий порядок. Нетрудно видеть, что условие положительности всех коэффициентов выполняется всегда, если выполнено условие , что будет при правильном согласовании направления вращения двигателя со знаком рассогласования.

Дополнительное условие , накладываемое на коэффициенты характеристического уравнения, сводится при подстановке значений коэффициентов , к неравенству

, (5.13)

которое является условием устойчивости рассматриваемой системы.

Из этого неравенства, в частности, можно заметить, что увеличение каждой постоянной времени сказывается отрицательно на устойчивости системы, так как при этом снижается предельное значение общего коэффициента усиления К , при котором система еще остается устойчивой.