5.3. Частотные критерии устойчивости

1. Критерий Михайлова

В основу критерия Михайлова, сформулированного им в 1938 г., положен известный в теории функций комплексного переменного принцип аргумента. Согласно этому принципу приращение аргумента функции комплексного переменного при изменении его по замкнутому контуру в положительном направлении (против часовой стрелки) составляет , где – число нулей, а – число полюсов функции внутри замкнутого контура. Предполагается, что функция аналитична внутри этого контура и не имеет нулей и полюсов на контуре.

Если применить принцип аргумента к полиному , стоящему в левой части характеристического уравнения

, (5.14)

используя в качестве контура мнимую ось , замкнутую полуокружностью бесконечного радиуса, то можно получить критерий Михайлова.

Однако предпочтем другое доказательство критерия Михайлова, которое является простым и поучительным. В соответствии с характеристическим уравнением полином можно представить в виде

, (5.15)

где – корни уравнения (1.1).

Положим , тогда

Рассмотрим геометрическое представление комплексных чисел на комплексной плоскости . Начала векторов, изображающих комплексные числа, лежат в точках , а концы – на мнимой оси в точке (рис. 5.3).

Найдем аргумент комплексного числа :

. (5.16)

Изменение аргумента с изменением равно

(5.17)

Согласно (5.17) для определения изменения аргумента необходимо подсчитать сумму изменений аргументов сомножителей . Изменения аргументов зависят от того, в какой (правой или левой) полуплоскости лежат корни . Рассмотрим два случая. Пусть корни лежат в левой полуплоскости (рис. 5.3, а). При изменении конец вектора скользит вдоль мнимой оси снизу вверх, поворачиваясь против часовой стрелки на 180º, при этом приращение аргумента

Если корень лежит в правой полуплоскости (рис. 5.3, б), то рассуждая аналогично, получим

Допустим, что уравнение имеет корней в правой полуплоскости и корней в левой полуплоскости (порядок уравнения равен ), тогда приращение аргумента при

(5.18)

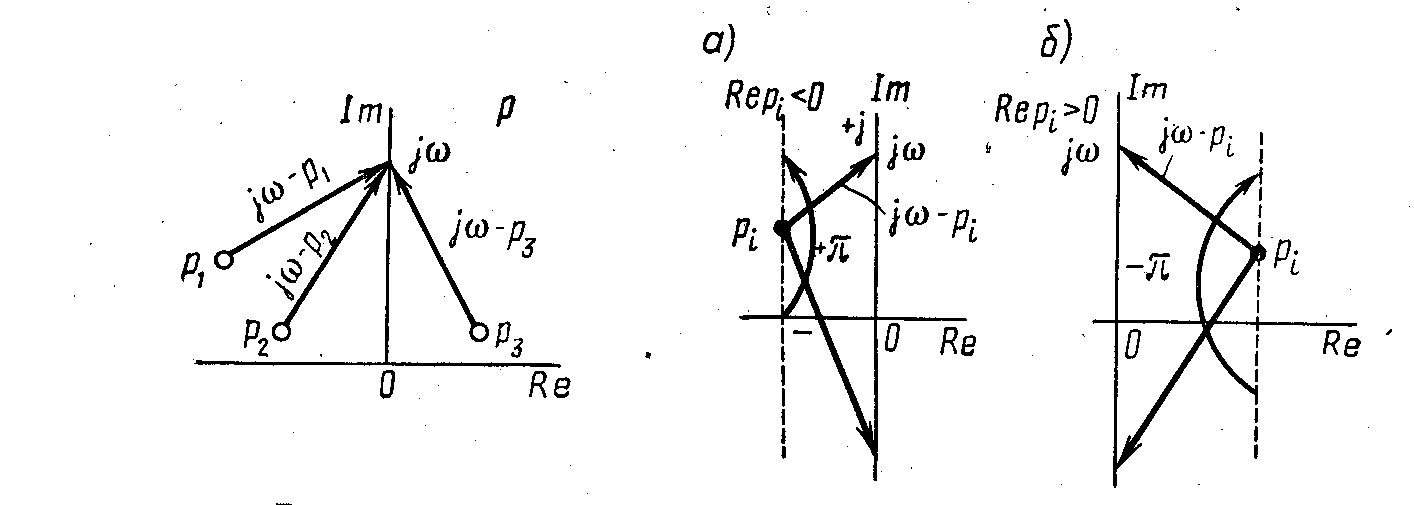
Рис. 5.3. Геометрическое представление комплексных чисел

Выражение (5.18) представляет собой запись принципа аргумента для характеристического полинома .

Для устойчивости системы автоматического регулирования, имеющей характеристическое уравнение , необходимо и достаточно, чтобы число правых корней было равно нулю; приращение аргумента при :

(5.19)

Заметим, что при аргумент будет монотонно возрастать с увеличением .

Критерий устойчивости Михайлова является наглядной графической интерпретацией соотношения (5.19). Построим годограф характеристического вектора , называемый годографом Михайлова. При этом можно ограничиться половинным диапазоном изменения , так как для полиномиальной функции от справедливы равенства

и часть годографа , соответствующая отрицательным значениям , представляет собой зеркальное отражение относительно действительной оси части годографа для положительных . При изменении в половинном диапазоне

(5.20)

Согласно критерию Михайлова для устойчивости системы автоматического регулирования необходимо и достаточно, чтобы годограф характеристического вектора , начинаясь при на действительной оси, с ростом от 0 до обходил последовательно в положительном направлении (против часовой стрелки) квадрантов, где – порядок характеристического уравнения.

На рис. 5.4, а показаны годографы Михайлова для устойчивых систем при различных значениях . Все они начинаются при со значения на положительной действительной полуоси. Это означает, что характеристические уравнения приведены к виду, при котором их коэффициенты положительны. Годографы, изображенные на рис. 5.4, а уходят в бесконечность при и обходят соответствующее число квадрантов в положительном направлении.

На рис. 5.4, б показаны годографы неустойчивых систем. Все они не удовлетворяют условию обхода квадрантов в положительном направлении.

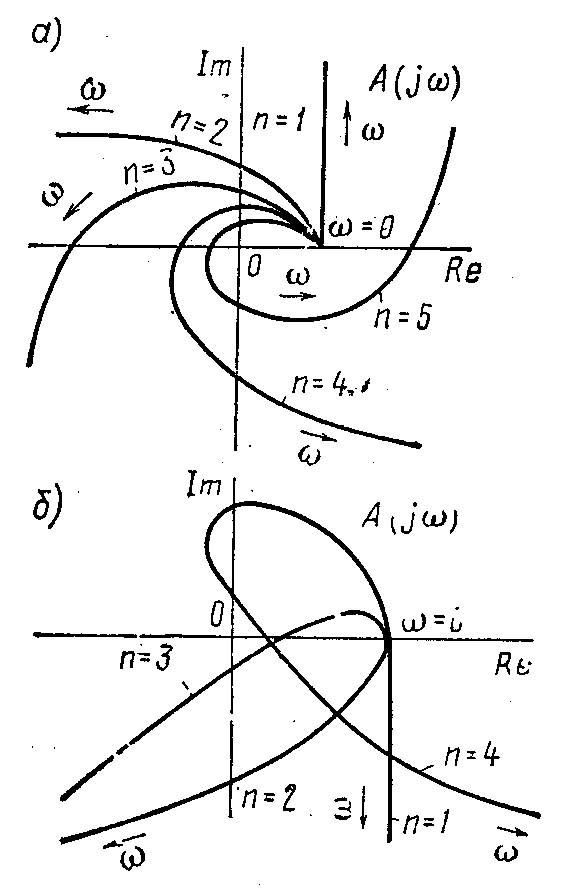
Рис. 5.4. Годографы Михайлова для устойчивых и неустойчивых систем