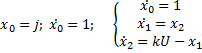- •Оптимальные и адаптивные системы (1 четверть).
- •Введение.
- •Глава 1. Принцип максимума Понтрягина (пмп).
- •Методика пмп.
- •Связь оптимального управления с энергией, запасаемой в объекте.
- •Теорема об n-интервалах.
- •Определение моментов переключения управляющих функций. Метод стыковки решения.
- •Задача об управлении консервативным объектом.
- •Аналитический синтез оптимальных регуляторов по квадратичному критерию качества.
- •Дискретная форма вариационной задачи. Принцип оптимальности Беллмана.
- •Непрерывная задача динамического программирования.
- •Глава 2. Общая характеристика адаптивных систем. Их классификация.
- •Типы самонастраивающихся систем (снс).
-
Связь оптимального управления с энергией, запасаемой в объекте.

![]()
![]()
![]()
![]() -
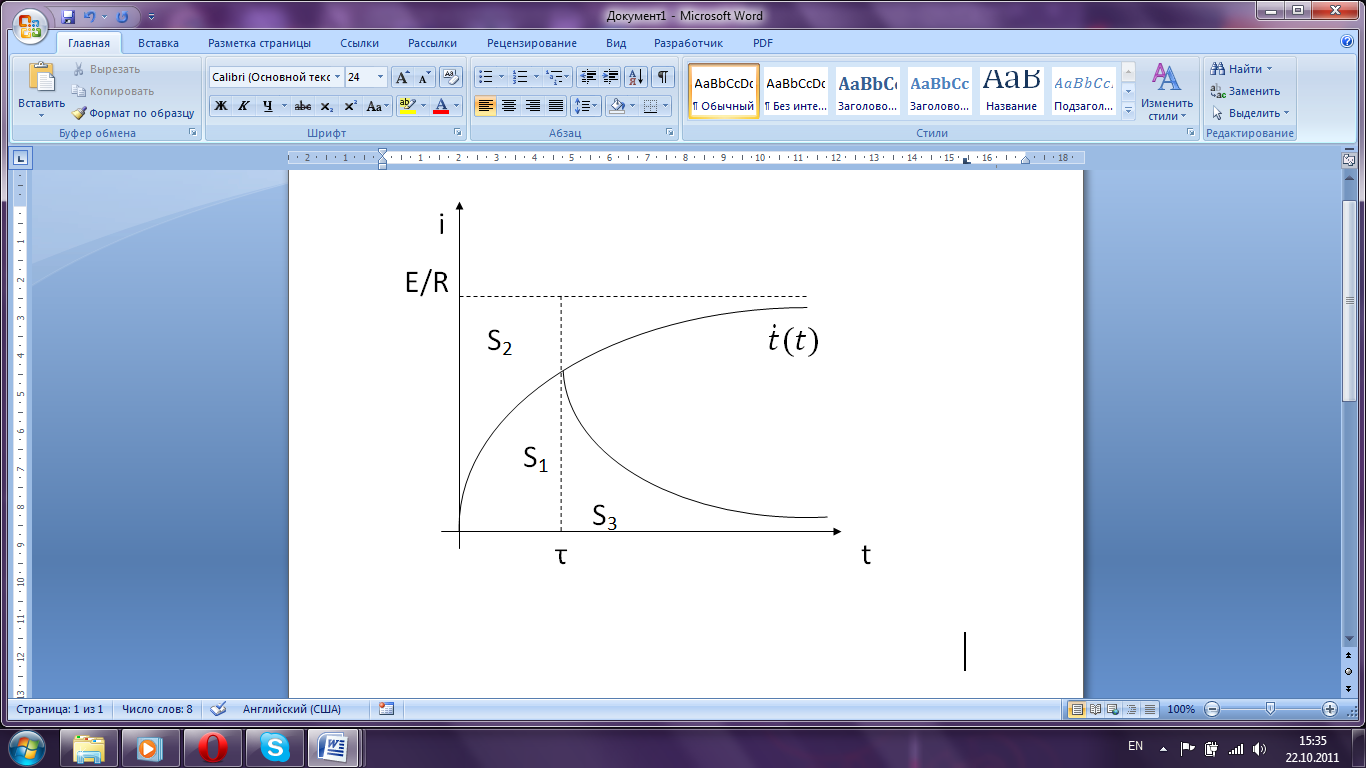
Энергия,
выделяемая за время (0, τ)на сопротивлении.
-
Энергия,
выделяемая за время (0, τ)на сопротивлении.
![]() – энергия, запасенная в катушке L.
– энергия, запасенная в катушке L.
![]()
S3 – энергия, рассеиваемая на сопротивлении, равная запасенной катушки.
![]()
Чтоб
система перенесла в новое установившееся
состояние ![]() ,
она должна запасти строго определенное
количество энергии
,
она должна запасти строго определенное
количество энергии ![]() .
.
Р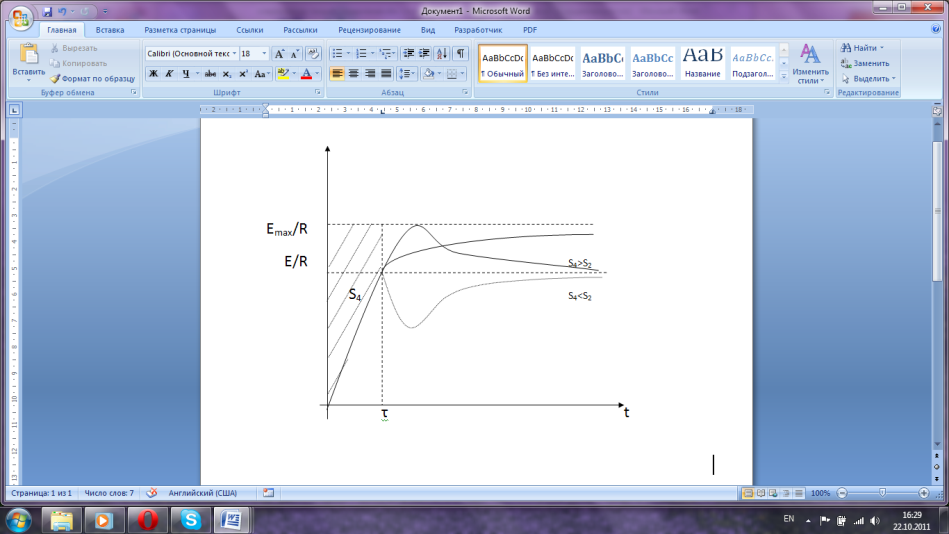
 ассмотрим
задачу скорейшего перевода этой системы
в желаемое состояние
ассмотрим
задачу скорейшего перевода этой системы
в желаемое состояние ![]() .
Пусть максимальное напряжение равно
Emax.
Для перевода в новое состояние применим
форсированное управление.
.
Пусть максимальное напряжение равно
Emax.
Для перевода в новое состояние применим
форсированное управление.
Вычислим S4 при форсированном управлении.
![]()
![]() .→
.→
![]()
![]()
П
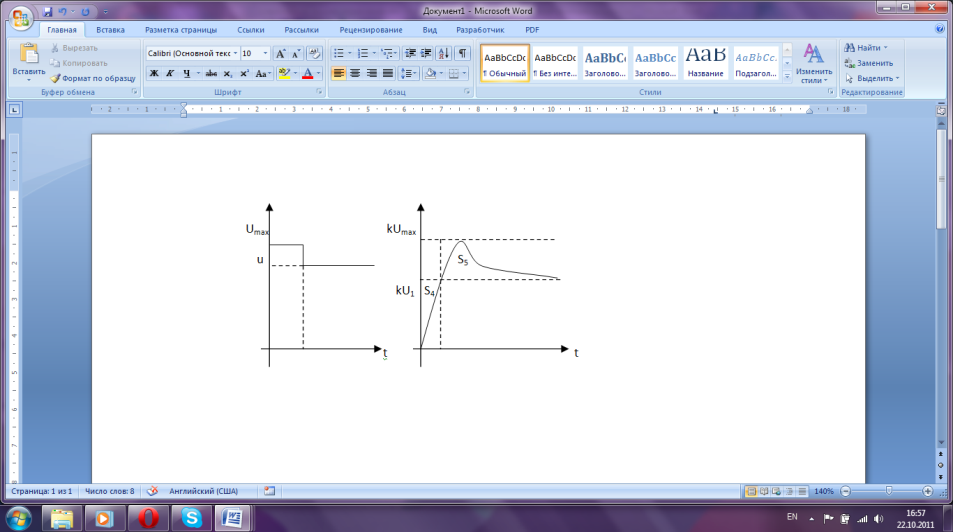 ри
форсированном управлении объектом
первого порядка количество запасаемой
энергии
ри
форсированном управлении объектом
первого порядка количество запасаемой
энергии ![]() строго соответствует необходимому для
установившегося состояния. Такое
управление справедливо для объекта
первого порядка. Рассмотрим объект
второго порядка:
строго соответствует необходимому для
установившегося состояния. Такое
управление справедливо для объекта
первого порядка. Рассмотрим объект
второго порядка: ![]() .
.
S2 – необходимое количество энергии.
Применим к этому объекту форсированное управление.
Можно
показать, что для объекта второго порядка
S4>S2
и поэтому процесс в момент времени τ не
прекращается. Чтоб обеспечить м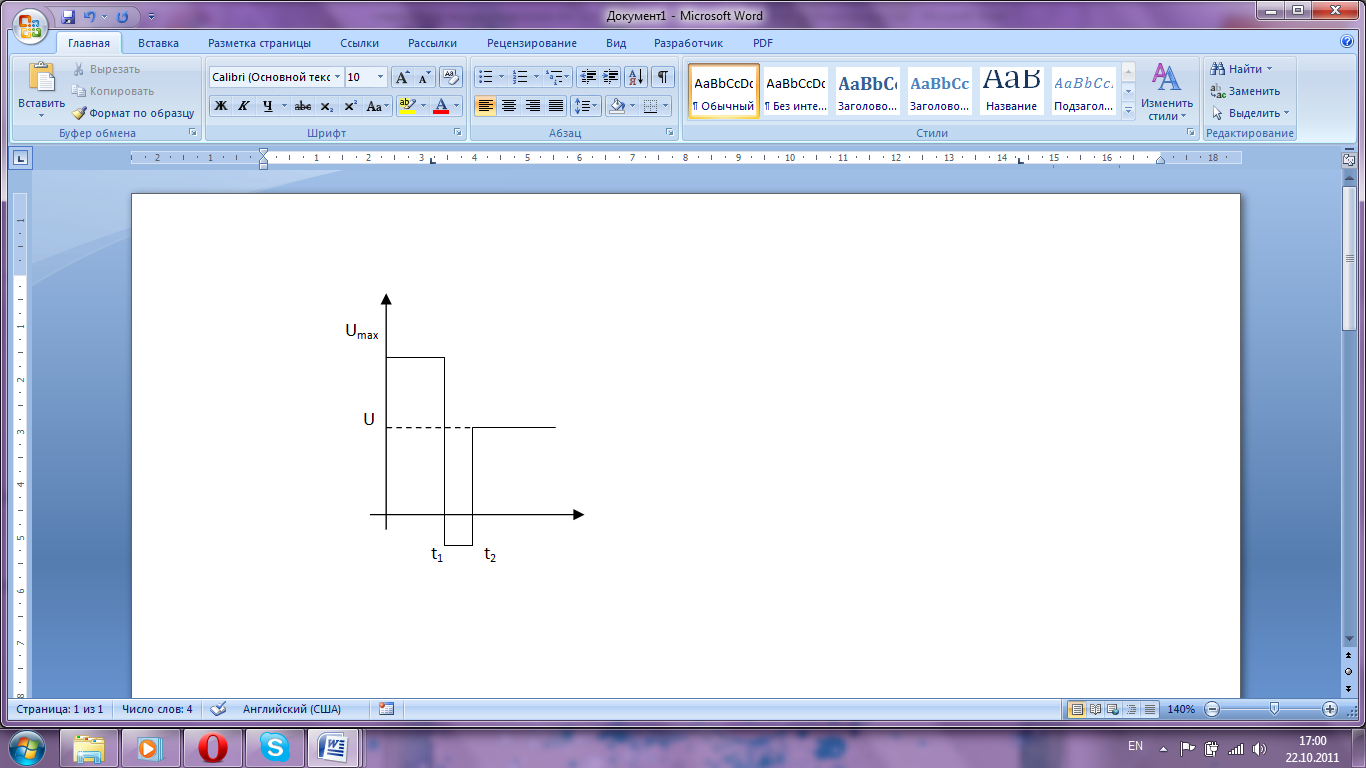 аксимальное
быстродействие для объекта 2го порядка
применяется управляющее воздействие
вида (излишек энергии тратится на
интервале (t1;
t2)).
аксимальное
быстродействие для объекта 2го порядка
применяется управляющее воздействие
вида (излишек энергии тратится на
интервале (t1;
t2)).
-
Теорема об n-интервалах.
Для
линейной системы n-го
порядка, у которой все корни
характеристического уравнения
действительны, а на управление наложены
ограничения по уровню ![]() ,
оптимальным, с точки зрения линейного
функционала будет управление, принимающее
граничные значения
,
оптимальным, с точки зрения линейного
функционала будет управление, принимающее
граничные значения ![]() и имеющее не более n
интервалов знакопостоянства.
и имеющее не более n
интервалов знакопостоянства.
-
ОУ – линейный.
-
Функционал – линейный.
-
Корни характеристического уравнения – действительны.
-
Управления ограничены по уровню.
-
Определение моментов переключения управляющих функций. Метод стыковки решения.
Суть метода рассмотрим на примере объекта 2го порядка:
![]() .
.
![]() (1)
(1)
Этот
объект необходимо перевести из начального
состояния ![]() в конечное
в конечное ![]() за минимальное время.
за минимальное время.
Корни характеристического уравнения действительные.
![]()
![]()
![]()
Общее
решение уравнения (1):
![]() .
Для определенности будем считать, что
.
Для определенности будем считать, что
![]() ,
значит
,
значит
![]() .
Найдем процессы
.
Найдем процессы ![]() ,
,
![]() на первом интервале при оптимальном
управлении:
на первом интервале при оптимальном
управлении:
![]()
Скорость
изменения: ![]()
Аналогично
для 2го интервала:
![]()
![]()
Для объекта
2го порядка функции y(t)
и ![]() будут непрерывные. В момент времени τ
должны выполнятся условия стыковки
будут непрерывные. В момент времени τ
должны выполнятся условия стыковки
![]() (4).
(4).
Имеется система с шестью неизвестными С11, С12, С21, С22, τ и T. Эти неизвестные определяются из системы шести нелинейных уравнений. Для их составления используются 4 граничных условия (2), (3) и условие стыковки (4).
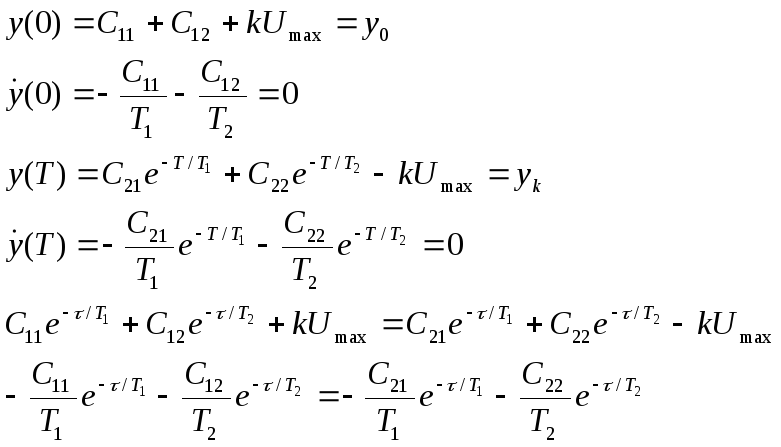
Для объекта порядка n имеем, при оптимальном управлении, n интервалов, n(n+1) уравнений и столько же неизвестных.
-
Задача об управлении консервативным объектом.
Если функционал не линеен или корни характеристического уравнения не действительны, то теорему об n интервалах применять нельзя. Рассмотрим пример. Имеется модель ОУ:
![]()
Этот объект нужно перевести из начального состояния в конечное за минимальное время:
![]()
При
ограничении на управлении: ![]() .
.
Решение.
n=2,
характеристическое уравнение ![]() .
Применяем для решения задачи методику
ПМП.
.
Применяем для решения задачи методику
ПМП.
![]()
![]()
![]()
![]()
![]()
![]()
Следовательно,
функция ![]() может менять знак более чем 2 раза.
Поэтому оптимальное управление U*
может содержать более 2х интервалов
постоянства.
может менять знак более чем 2 раза.
Поэтому оптимальное управление U*
может содержать более 2х интервалов
постоянства.