Вопросы для самопроверки

1. Что называют начальным моментом k-го порядка случайной величины?

2. По какой формуле вычисляются начальные моменты k-го порядка случайной величины, принимающей конечное множество значений?

3. Какой формулой определяется начальный момент k-го порядка случайной величины, принимающей счетное множество значений?

4. Какой формулой определяется начальный момент k-го порядка непрерывной случайной величины?

5. Что называется центральным моментом k-го порядка случайной величины?

6. По какой формуле вычисляется центральный момент k-го порядка случайной величины, принимающей конечное множество значений?

7. Какой формулой определяется центральный момент k-го порядка случайной величины, принимающей счетное множество значений?

8. Какой формулой определяется центральный момент k-го порядка непрерывной случайной величины?

9. Чему равны начальные моменты нулевого порядка, первого порядка?

10. Чему равны центральные моменты нулевого, первого, второго порядков?

11. Как выражаются центральные моменты второго порядка через начальные моменты?

12. Как выражаются центральные моменты третьего порядка через начальные моменты?

Упражнения

1. Дискретная случайная величина задана законом распределения

а)	Х	2 3		б)	Х	1 2 3 4 5
	Р	0,4   0,6			Р	0,1   0,2 0,4 0,2 0,1

Найти начальные и центральные моменты первого, второго и третьего порядков случайной величины.

2. Случайная величина задана плотностью распределения

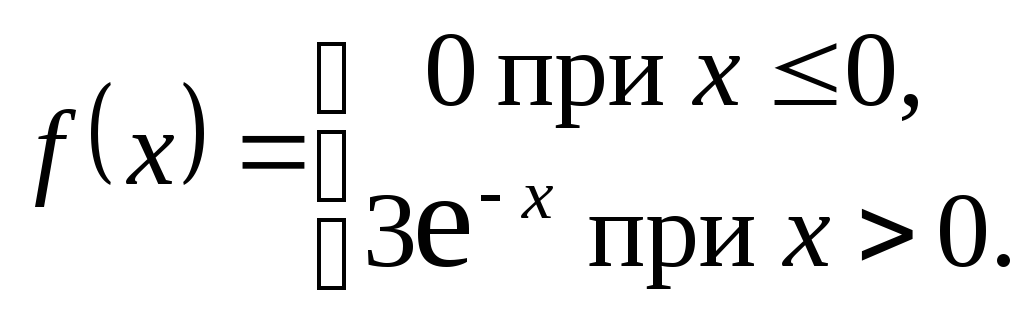
Найти начальные и центральные моменты первого, второго, третьего и четвертого порядков.

3. Случайная величина Х задана плотностью распределения

а) б)

Найти начальные и центральные моменты.

4. Случайная величина задана функцией распределения

а) б)

Найти начальные и центральные моменты первых трех порядков случайной величины.

4. Некоторые законы распределения случайных величин

4.1. Формула Бернулли

Производятся испытания, в каждом из которых может появиться событие А или событие Ā. Если вероятность события А в одном испытании не зависит от появления его в любом другом, то испытания называются независимыми относительно события А. Будем считать, что испытания происходят в одинаковых условиях и вероятность появления события А в каждом испытании одна и та же. Обозначим эту вероятность через р, а вероятность появления события Ā через .

Вероятность того, что в серии из п независимых испытаний событие А появится ровно k раз (и не появится п-k раз), обозначим через , тогда

– это формула Бернулли. Правая часть ее представляет собой общий член разложения бинома Ньютона

.

Поскольку , то сумма всех биномиальных вероятностей равна единице:

.

Число k₀, которому при заданном п соответствует максимальная биномиальная вероятность P_n(k₀), называется наивероятнейшим числом появления события А. При заданных п и р это число определяется неравенствами

.

Если число не является целым, то равно целой части этого числа; если же – целое число, то имеет два значения: и .

Вероятность того, что в п опытах схемы Бернулли событие А появится от до раз, равна

.

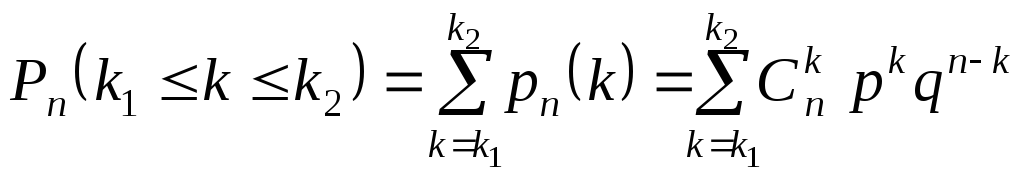Вероятность того, что в п опытах событие А появится хотя бы один раз, определяется формулой

.

Вероятность того, что в п испытаниях событие А наступит: а) менее k раз, в) более k раз, в) не менее k раз, г) не более k раз, находят соответственно по формулам:

Производится п независимых опытов, каждый из которых имеет попарно несовместных и единственно возможных исходов с вероятностями , одинаковыми во всех опытах .

Для произвольных целых неотрицательных чисел обозначим через вероятность того, что в п опытах исход А₁ наступит k₁ раз, исход раз, …, исход раз, тогда

.

Эта формула определяет полиноминальное распределение вероятностей. Биномиальное распределение является частным случаем полиноминального распределения при .

Пример 4.1.1. Всхожесть семян равна 90%. Найти вероятность того, что из четырех посеянных семян взойдут а) три; б) не менее трех.

Искомые вероятности находим с помощью формулы Бернулли. В первом случае поэтому

.

Во втором случае событие А состоит в том, что из четырех семян взойдут или три, или четыре. По теореме сложения вероятностей

.

Поскольку

то Р(А) = 0,2916 + 0,6561 = 0,9477.

Пример 4.1.2. Доля изделий высшего сорта на данном предприятии составляет 30%. Чему равно наивероятнейшее число изделий высшего сорта в случайно отобранной партии из 75 изделий?

,

отсюда