
- •В. А. Шкель высшая математика Случайные величины
- •Ключевые слова
- •1. Виды случайных величин. Закон распределения вероятностей дискретной случайной величины
- •Вопросы для самопроверки
- •Упражнения
- •2. Функция распределения вероятностей случайной величины
- •Вопросы для самопроверки
- •Упражнения
- •3. Плотность распределения вероятностей непрерывной случайной величины
- •Вопросы для самопроверки
- •Упражнения
- •Ключевые слова
- •1. Математическое ожидание случайной величины, мода, медиана
- •Вопросы для самопроверки
- •Упражнения
- •2. Дисперсия случайной величины. Среднее квадратическое отклонение
- •Свойства дисперсии
- •Вопросы для самопроверки
- •Упражнения
- •3. Моменты случайных величин
- •Вопросы для самопроверки
- •Упражнения
- •4. Некоторые законы распределения случайных величин
- •4.1. Формула Бернулли
- •Вопросы для самопроверки
- •Упражнения
- •4.2. Биномиальное распределение
- •Вопросы для самопроверки
- •Упражнения
- •4.3. Распределение Пуассона
- •Вопросы для самопроверки
- •Упражнения
- •4.4. Равномерное распределение
- •Вопросы для самопроверки
- •Упражнения
- •4.5. Нормальное распределение
- •Вопросы для самопроверки
- •Упражнения
- •4.6. Некоторые другие распределения
- •Вопросы для самопроверки
- •Упражнения
- •Литература
- •Содержание
- •1. Виды случайных величин. Закон распределения вероятностей дискретной случайной величины 3
- •2. Функция распределения вероятностей случайной величины 10
- •3. Плотность распределения вероятностей непрерывной случайной величины 16
- •Шкель Всеволод Ануфриевич высшая математика Случайные величины
- •220086, Г. Минск, ул. Славинского, 1, корп. 3.
Упражнения
1. Случайная
величина Х
распределена по нормальному закону,
причем
![]() .
Найти
.
Найти
![]() ,
если известно
,
если известно
![]() .
.
2. Автомат
изготавливает подшипники, которые
считаются годными, если отклонение Х
от проектного размера по модулю не
превышает 0,77 мм. Каково наиболее вероятное
число годных подшипников из 100, если
случайная величина Х
распределена нормально с параметром
![]() мм?
мм?
3. Станок-автомат
изготавливает валики, контролируя их
диаметры Х.
Считая, что случайная величина Х
распределена нормально с параметрами
![]() мм,
мм,
![]() мм,
найти интервал, в котором с вероятностью
0,9973 будут находиться диаметры изготовленных
валиков.
мм,
найти интервал, в котором с вероятностью
0,9973 будут находиться диаметры изготовленных
валиков.
4. Найти
![]() для случайной величины, распределенной
по нормальному закону с параметрами а
и
для случайной величины, распределенной
по нормальному закону с параметрами а
и
![]() .
.
5. Случайная величина Х распределена по нормальному закону. Математическое ожидание и дисперсия этой величины соответственно равны 7 и 16. Найти вероятность того, что отклонение величины Х от ее мате-матического ожидания по модулю не превзойдет двух.
6. Среднее квадратическое отклонение случайной величины, распределенной по нормальному закону, равно 2 см, а математическое ожидание равно 16 см. Найти границы, в которых с вероятностью 0,95 следует ожидать значение случайной величины.
4.6. Некоторые другие распределения
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью вероятностей
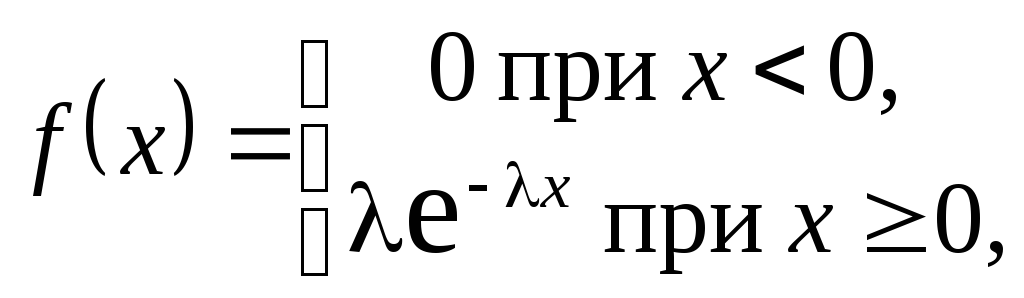
где
![]() – постоянная положительная величина.
– постоянная положительная величина.
Показательный закон распределения вероятностей встречается во многих задачах, связанных с простейшим потоком событий. Под потоком событий понимают последовательность событий, наступающих одно за другим в случайные моменты. Например, поток вызовов на телефонной станции, поток заявок в системе массового обслуживания и др.
Функция распределения показательного закона имеет вид
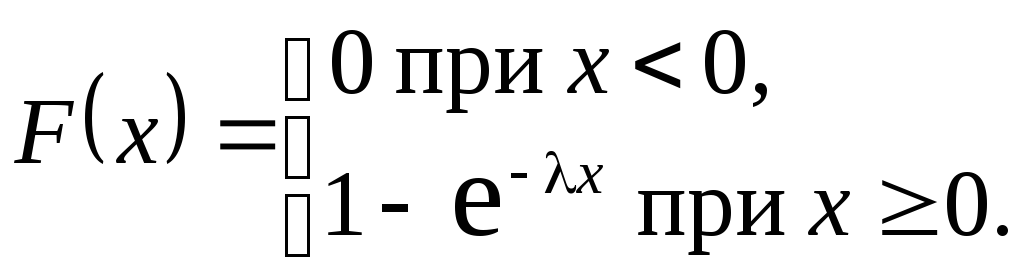
![]()
Вероятность
попадания в интервал
![]() непрерывной случайной величины
Х, которая
распределена по показательному закону,
равна
непрерывной случайной величины
Х, которая
распределена по показательному закону,
равна
 .
.
Нетрудно вычислить числовые характеристики показательного распределения:
![]() ,
,
![]() ,
,
![]() .
.
Пример
4.6.1.
Непрерывная величина Х
распределена по показательному закону:
![]() при
при
![]() ,
,
![]() .
Найти вероятность попадания значений
величины Х
в интервал
.
Найти вероятность попадания значений
величины Х
в интервал
![]() .
.

Пример
4.6.2. Найти
математическое ожидание, дисперсию и
среднее квадратическое отклонение
случайной величины Х,
плотность распределения которой задана
функцией
![]() .
.
![]() .
.
Дискретная случайная
величина Х
имеет геометрическое распределение,
если она принимает значения
![]() (счетное множество значений) с вероятностями
(счетное множество значений) с вероятностями
![]()
![]() .
.
Определение является корректным, так как сумма вероятностей
![]() .
.
Случайная величина Х, имеющая геометрическое распределение, представляет собой число испытаний Бернулли до первого успеха.
Математическое ожидание и дисперсия Х:
![]()
Пример 4.6.3. В большой партии изделий вероятность брака равна р. Контроль качества проводится до первого появления бракованного изделия. Обнаружилось, что бракованное изделие впервые появилось в среднем при десятом испытании. Оценить вероятность р.
Пусть Х
– число испытаний до первого появления
бракованного изделия. Эта случайная
величина имеет геометрическое
распределение. По условию ее среднее
значение равно
![]() Так как
Так как
![]() то
то
![]() .
.
Дискретная случайная величина имеет гипергеометрическое распределение, если она принимает значения т с вероятностями
 ,
,
где
![]()
Вероятность
![]() является вероятностью выбора m
объектов, обладающих заданным свойством,
из множества п
объектов, случайно извлеченных (без
возврата) из совокупности N
объектов, среди которых М
объектов обладают заданным свойством.
является вероятностью выбора m
объектов, обладающих заданным свойством,
из множества п
объектов, случайно извлеченных (без
возврата) из совокупности N
объектов, среди которых М
объектов обладают заданным свойством.
Математическое ожидание и дисперсия случайной величины, имеющей гипергеометрическое распределение с параметрами п, М, N:
![]()
Пример 4.6.4. Среди продукции цеха электронных плат 10 из партии в 100 штук не удовлетворяют стандарту. При приемке продукции проверяются 10 плат. Какое среднее количество нестандартных плат обнаружат?
Количество нестандартных плат имеет гипергеометрическое распределение, так как
![]() то
то
![]()
