УДК 004.4

ББК 32.973-018

Р 28

Рекомендовано к изданию редакционно-издательским советом Частного института управления и предпринимательства

Автор

доцент кафедры высшей математики и статистики

Частного института управления и предпринимательства

кандидат физико-математических наук Н. Н. Рачковский

Рецензенты:

доцент кафедры экономики и управления бизнесом Государственного института управления и социальных технологий БГУ кандидат физико-математических наук, доцент Т. В. Веремеенко;

доцент кафедры алгебры и геометрии Белорусского государственного педагогического университета им. М. Танка кандидат физико-математических наук, доцент В. А. Янцевич

Рассмотрено и одобрено на заседании

кафедры высшей математики и статистики,

протокол № 10 от 11.05.2007 г.

Рачковский, Н. Н.

Р 28 Математическое программирование: Транспортная задача: учеб.-метод. пособие / Н. Н. Рачковский. – Минск: Частн. ин-т управ. и предпр., 2007.– 29 с.

Рассматриваются обеспечение разрешимости транспортной задачи и построение начального плана перевозок. Дается теоретическое обоснование метода потенциалов. Приводится решение транспортной задачи.

Для студентов Частного института управления и предпринимательства.

УДК 004.4

ББК 32.973-018

© Рачковский Н. Н., 2007

© Частный институт управления и предпринимательства, 2007

Лекция. Транспортная задача План:

1. Постановка задачи и ее математическая модель.

2. Обеспечение разрешимости транспортной задачи. Построение начального плана перевозок.

3. Теоретическое обоснование метода потенциалов.

4. Алгоритм метода потенциалов.

5. Пример решения транспортной задачи.

6. Упражнения для самостоятельной работы.

Ключевые слова:

транспортная задача; математическая модель; метод северо-западного угла; метод потенциалов;

симплекс-метод; распределительная таблица; начальный план перевозок

1. Постановка задачи и ее математическая модель

Пусть имеется m поставщиков А₁, А₂, … , А_m некоторого однородного груза, накопленного ими в объемах а₁, а₂, …, а_m соответственно. Пусть имеется n потребителей В₁, В₂, … , В_n со спросом на этот груз в объемах b₁, b₂, … , b_n. Известны тарифы перевозок C_ij – стоимость перевозки одной единицы груза от каждого поставщика А_j к каждому потребителю B_j. Требуется найти оптимальный план перевозок, обеспечивающий:

а) полный вывоз накопленного груза (по возможности) из всех пунктов поставки А₁, А₂, … , А_m;

б) полное удовлетворение спроса (по возможности) всех потребителей В₁, В₂, … , В_n;

в) минимальные транспортные расходы.

Условие такой задачи принято записывать в виде таблицы (табл. 1):

Таблица 1

		Потребители	Накопленный запас груза
Поставщики
Спрос

Чтобы решить сформулированную выше задачу с помощью математического аппарата, нужно составить математическую модель, создание которой осуществляется в три этапа:

1) выбор переменных;

2) создание целевой функции;

3) составление ограничений.

В качестве переменных рассмотрим – количество единиц груза, перевозимого от каждого поставщика к каждому потребителю . Нетрудно понять, что переменных будет . В качестве целевой функции рассмотрим то, что нужно минимизировать – транспортные расходы. Учитывая, что в условии задачи даны тарифы перевозок, получим целевую функцию

.

Первую часть ограничений составим исходя из условия вывоза всего накопленного груза от каждого поставщика . Понятно, что таких ограничений будет столько, сколько имеется поставщиков, т. е. m. Учитывая условие задачи и выбранные выше переменные, получим следующие ограничения:

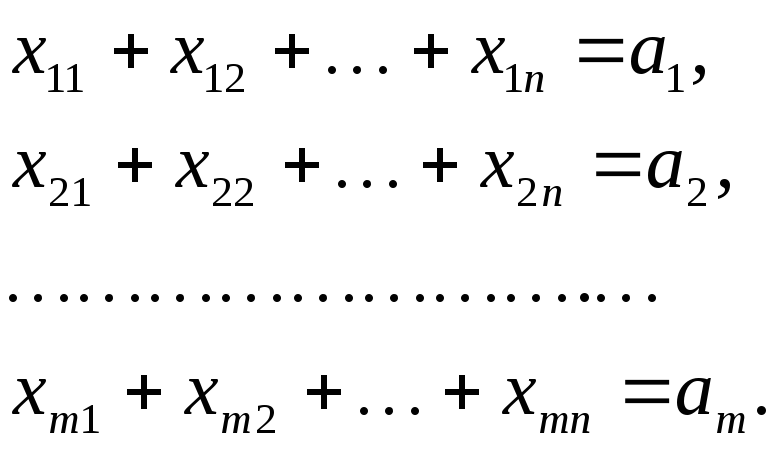
Вторую часть ограничений составим исходя из условия полного удовлетворения спроса всех потребителей . Ограничений будет столько, сколько имеется потребителей, т. е. n. С учетом условия задачи и выбранных переменных получим следующие ограничения:

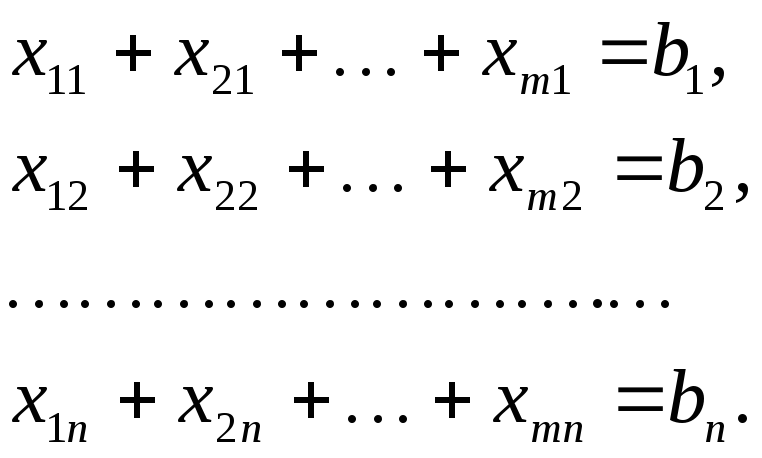
Третью часть ограничений составим исходя из экономического смысла переменных – количество перевозимого груза не может быть отрицательным, т. е. все . Получаем следующую математическую модель транспортной задачи:

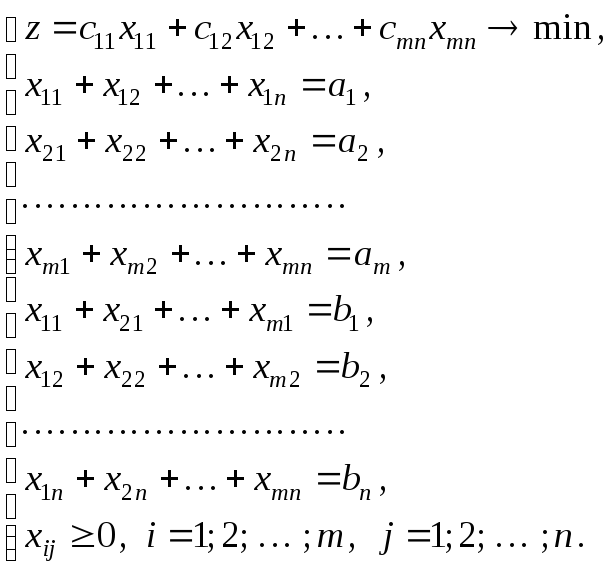
Построенная математическая модель является задачей линейного программирования, поэтому может быть решена симплекс–методом. Из-за большого количества переменных и ограничений–уравнений даже при относительно небольших значениях m и n (например, при и получаем задачу линейного программирования с девятью переменными и шестью ограничениями–уравнениями) использование стандартного варианта симплекс–метода затруднено по причине большого количества громоздких вычислений. Однако специфичность ограничений-уравнений (каждая переменная присутствует только в двух уравнениях и только с коэффициентом +1) позволяет значительно упростить вычисления. Эти упрощения приводят к адаптированной модификации симплекс-метода, называемой методом потенциалов, которая используется при решении транспортной задачи.