
- •IX. Релятивистская механика
- •1. Кинематика
- •Решение задач
- •2. Динамика
- •Решение задач
- •X. Механические колебания
- •1. Кинематика незатухающих колебаний
- •Решение задач
- •2. Энергия незатухающих колебаний (на примере пружинного маятника)
- •3. Динамика незатухающих колебаний материальной точки
- •Решение задач
- •4. Динамика незатухающих колебаний твёрдого тела.
- •Решение задач
- •5. Затухающие колебания.
- •Решение задач
- •6. Вынужденные колебания.
- •Решение задач
X. Механические колебания
1. Кинематика незатухающих колебаний
Уравнение, описывающее положение точки, совершающей гармонические колебания, имеет следующий вид:
![]() ,
,
где
x
- смещение точки из положения равновесия
в момент t
(в зависимости от характера движения
это может быть либо линейная, либо
угловая координата); A
- амплитуда колебаний, то есть максимальное
смещение точки из положения равновесия;
![]() - фаза колебаний;
- фаза колебаний;
![]() - начальная фаза, которая характеризует
положение точки в момент t = 0
(начало наблюдения);
- начальная фаза, которая характеризует
положение точки в момент t = 0
(начало наблюдения);
![]() -
круговая частота колебаний. Эта частота
связана с периодом колебаний T
соотношением
-
круговая частота колебаний. Эта частота
связана с периодом колебаний T
соотношением
![]() .
.
Приведённое выше уравнение является решением дифференциального уравнения
![]() ,
,
которое будет обсуждаться ниже.
Решение задач
10.1.
Точка
совершает колебания вдоль оси X
по закону
![]() .
Найти зависимость от времени скорости
.
Найти зависимость от времени скорости
![]() и ускорения
и ускорения
![]() .
Как связаны амплитуды скорости
.
Как связаны амплитуды скорости
![]() и ускорения
и ускорения
![]() с амплитудой смещения A.
с амплитудой смещения A.
Решение. Закон движения точки в общем виде известен
![]() .
.
Законы изменения скорости и ускорения со временем найдем последовательным дифференцированием по времени исходного уравнения
![]() ,
откуда
,
откуда
![]() ;
;
![]() или
или
![]() ,
откуда
,
откуда
![]() .
.
10.2.
Частица совершает гармонические
колебания вдоль оси X
около положения равновесия x = 0.
В некоторый момент времени координата
частицы x0,
а скорость
![]() .
Найти координату x
и скорость
.
Найти координату x
и скорость
![]() частицы через время t
после этого момента.
частицы через время t
после этого момента.
Решение. Частица совершает гармонические колебания по закону
![]() ,
,
тогда
![]() .
.
Пусть
в начальный момент времени t = 0
координата частицы x0,
а ее скорость
![]() .
Тогда
.
Тогда
![]() и
и
![]() ,
,
![]() ,
,
![]() .
.
Откуда начальная фаза равна
![]() .
.
В начальный момент времени (t = 0)
![]() ,
поэтому
,
поэтому
![]() ;
;
![]() ,
поэтому
,
поэтому
![]() .
.
Воспользовавшись
основным тригонометрическим тождеством
![]() ,
запишем
,
запишем
 .
.
Откуда амплитуда равна
 .
.
Подставив найденные значения амплитуды и начальной фазы в исходные уравнения, получим
 ,
,
 .
.
10.3. Точка совершает гармонические колебания вдоль некоторой прямой с периодом T и амплитудой A. Найти среднюю скорость точки за время, в течение которого она проходит путь A/2:
а) из крайнего положения;
б) из положения равновесия.
Решение.
а) По
определению средней скорости
![]() ,
где S
- путь, пройденный за время
t.
В данном случае
,
где S
- путь, пройденный за время
t.
В данном случае
![]() ,
,
где
t1
- время движения точки из крайнего
положения, где смещение из положения
равновесия равно A,
до положения, где это смещение равно
A/2.
Пусть в момент времени t = 0
смещение максимально (крайнее положение).
Это возможно, если смещение зависит от
времени по закону
![]() ,
тогда:
,
тогда:
![]() ,
,
![]() ,
,
поэтому
![]() ,
а
,
а
![]() .
.
Подставив полученное значение в исходное уравнение, найдем среднюю скорость
![]() .
.
б)
В данном случае за t = 0
принимаем момент, когда точка проходит
положение равновесия (x = 0),
тогда
![]() и, следовательно
и, следовательно
![]() ,
,
![]() ,
,
откуда
![]() ,
а
,
а
![]() .
.
а искомая средняя скорость равна
![]() .
.
Если
тело участвует одновременно в нескольких
колебаниях, то решение многих задач
упрощается, если сложение колебаний
производить графически методом векторных
диаграмм. Пусть точка совершает колебания
по закону
![]() .
Графически это колебание представляется
как вектор длиной A,
который равномерно вращается против
ча
.
Графически это колебание представляется
как вектор длиной A,
который равномерно вращается против
ча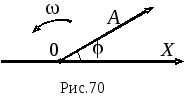 совой
стрелки с постоянной угловой скоростью
совой
стрелки с постоянной угловой скоростью
![]() от начального углового положения
от начального углового положения
![]() (рис.70). В этом случае угол с осью X
меняется по закону
(рис.70). В этом случае угол с осью X
меняется по закону
![]() ,
а проекция вектора на ось X
и будет равна координате
,
а проекция вектора на ось X
и будет равна координате
![]() .
.
10.4. Найти графически амплитуду A колебаний, которые возникают при сложении двух колебаний одного направления:
![]() ,
,
![]() .
.
Решение.
Оба вектора
будут вращаться с одинаковой угловой
скоростью
![]() .
Следовательно, угол между векторами
остается постоянным в любой момент
времени. Воспользовавшись формулами
приведения, представим второе
колебание в виде:
.
Следовательно, угол между векторами
остается постоянным в любой момент
времени. Воспользовавшись формулами
приведения, представим второе
колебание в виде:
![]() .
.
 Уравнение
гармонического колебания имеет вид
Уравнение
гармонического колебания имеет вид
![]() .
.
Из сравнения уравнений колебаний с уравнением гармонического колебания, найдем начальные фазы первого и второго колебаний
![]() и
и
![]() .
.
Теперь построим векторную диаграмму (рис.71). Согласно теореме косинусов получим
![]() .
.
Из
рисунка видно, что
![]() ,
тогда искомая амплитуда равна
,
тогда искомая амплитуда равна
![]() ,
,
![]() .
.
