§ 5. Скалярное произведение

Определение. Скалярным произведением векторов и называется число .

Свойства скалярного произведения

1. .

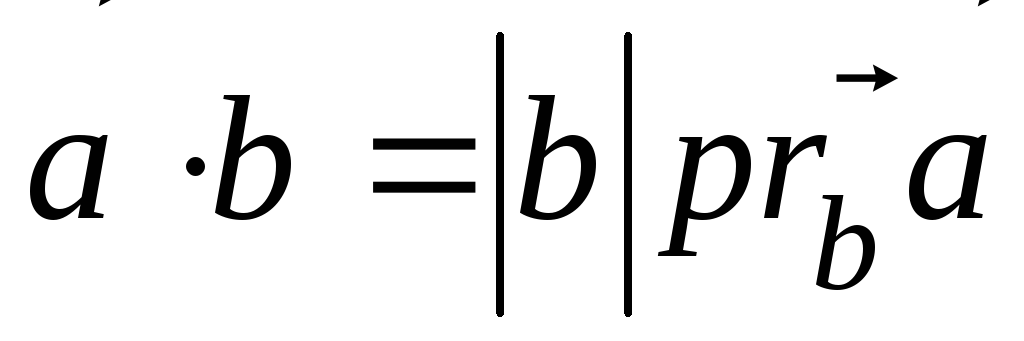►Если , то равенство очевидно. Если же , то оно вытекает из определения скалярного произведения и свойств пропорций: .◄

2. .

3. .

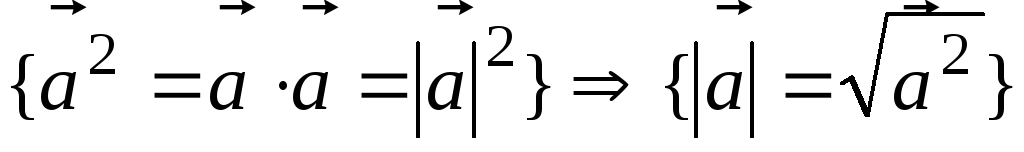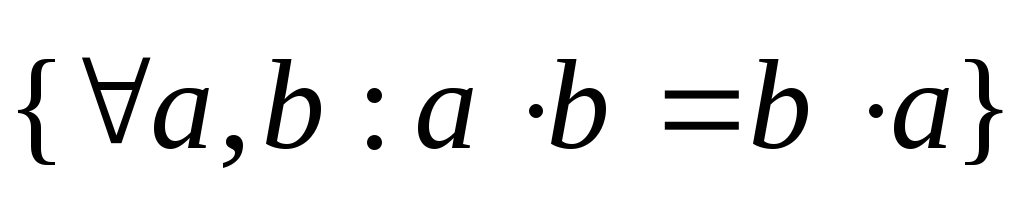Эти два свойства очевидным образом вытекают из определения.

4. .

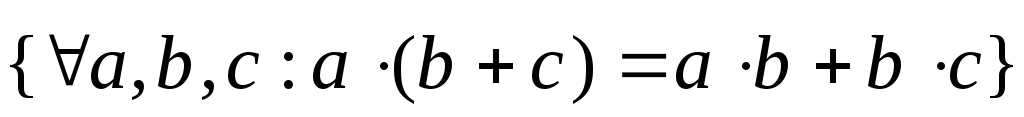►Если , то равенство очевидно. Если же , то .◄

5. 

Доказывается так же, как и четвертое свойство.

6. .

►◄

7. .

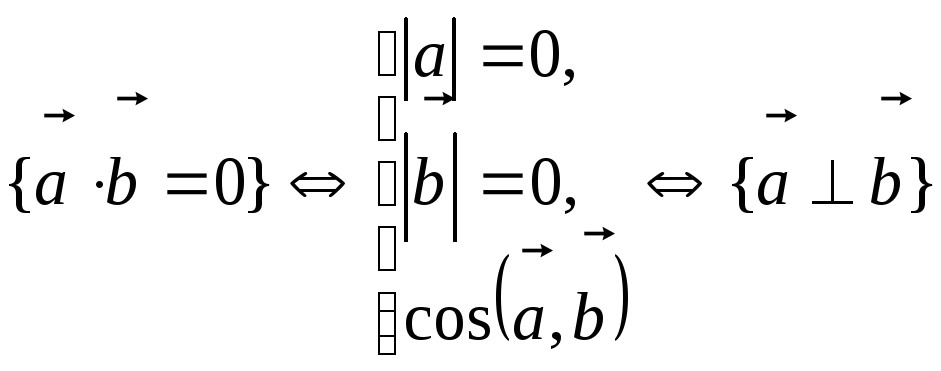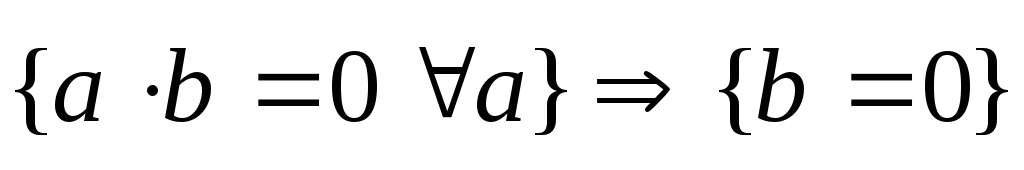►Положим . Тогда .◄

8. .

►.◄

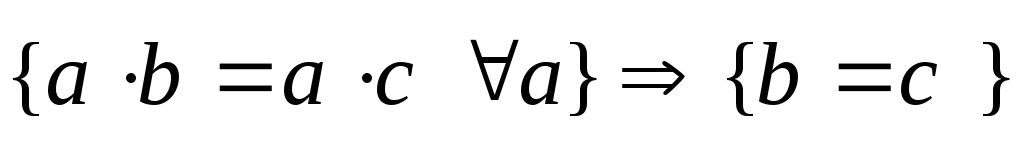Из 4-го и 5-го свойств скалярного произведения также вытекает, что линейные комбинации векторов можно перемножать скалярно по правилу умножения многочленов, т.е. так, как вы в школе обычно раскрывали скобки. Например, .

Выражение скалярного произведения через координаты перемножаемых векторов в ортонормированном базисе

Сначала заметим, что, , а в силу ортонормированности базиса. Пусть теперь заданы два вектора и своими координатами в базисе . Тогда

. .

Таким образом, в ортонормированном базисе скалярное произведение вычисляется как сумма произведении соответствующих координат перемножаемых векторов. Из этой же формулы при получаем: , т.е. в ортонормированном базисе длина вектора равна

вычисление в ортонормированном базисе корню квадратному из суммы квадратов его координат.

§6. Векторное произведение Определение векторного произведения.

В екторным произведением векторов и , взятых в указанном порядке, называется вектор, который обозначается и удовлетворяет следующим условиям:

1. .

2. .

3. Ориентация тройки векторов совпадает с ориентацией выбранного базиса.

Так как мы договорились рассматривать правые базисы, то в нашем случае – правая тройка (рис. 1.22).

Свойства векторного произведения

1. (критерий коллинеарности).

►.◄

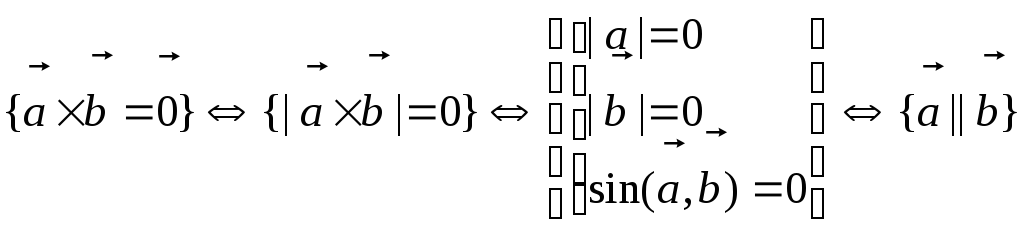2. – антикоммутативность.

►а) .

б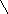) 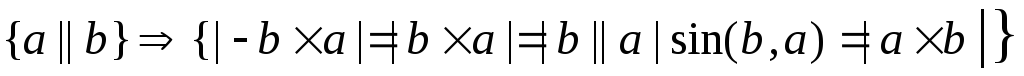. Кроме того, если , то существует плоскость P такая, что , поэтому , а значит, и . Итак, . Остаётся убедиться в сонаправленности этих векторов.

{-правая} левая} 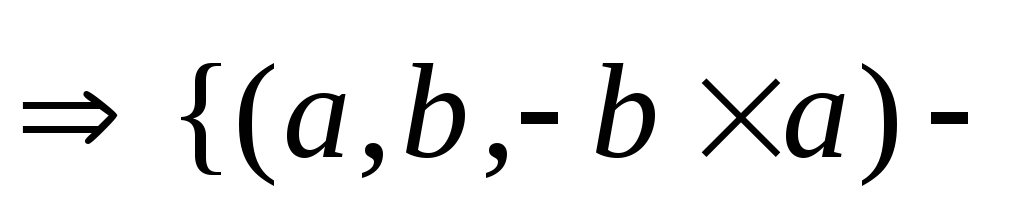правая}

.

Таким образом, длины и направления векторов и совпадают, значит .◄

3. , .

4.

Эти два свойства мы докажем в § 7.

5. Линейные комбинации векторов векторно умножаются по правилу умножения многочленов. При этом не следует забывать, что сомножитель из первой скобки обязательно должен быть на первом месте.

Это свойство является следствием 3-го и 4-го.

Пример. ▼

.▲

6. Геометрический смысл векторного произведения: модуль векторного произведения неколлинеарных векторов численно равен площади параллелограмма, построенного на этих векторах, отложенных от одной точки.

7. Физический смысл векторного произведения. Моментом силы , приложенной к точке А, относительно точки О является вектор .

Выражение векторного произведения через координаты перемножаемых векторов в ортонормированном базисе

Сначала составим таблицу векторного умножения базисных векторов. Векторы первого столбца будем считать первыми сомножителями, а векторы верхней строчки – вторыми. Согласно критерию коллинеарности, . Очевидно, , . Кроме того, т.к. тройка векторов - правая, то , . Аналогично заполняются остальные клетки.

Пусть теперь заданы два вектора и своими координатами в базисе . Тогда

. (1)

Для облегчения запоминания этой формулы введем понятие определителя второго и третьего порядка (подробно теория определителей будет изучаться в линейной алгебре).

Определитель второго порядка записывается в виде таблицы, ограниченной вертикальной чертой с обеих сторон, и вычисляется следующим образом:

Здесь первый индекс обозначает номер строки, а второй – номер столбца.

Определитель третьего порядка вычисляется так:

.

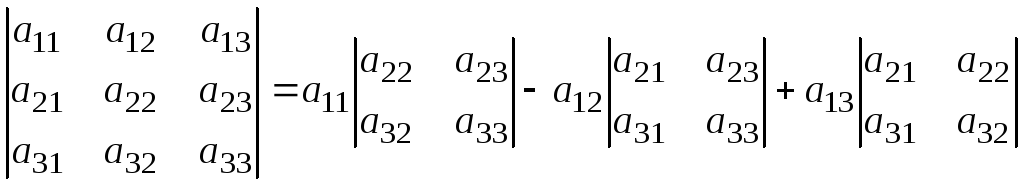Теперь из (1) получаем:

.

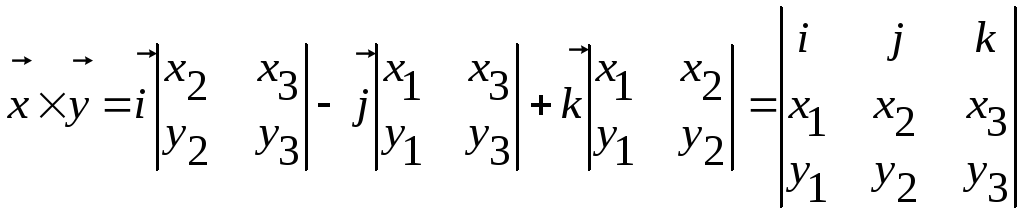Это и есть та формула, которую вы должны запомнить.