Ориентация тройки векторов
Упорядоченная
тройка некомпланарных векторов называется
правой,
если, глядя с конца третьего вектора на
плоскость первых двух, мы видим поворот
от первого вектора ко второму по
кратчайшему
пути происходящим против часовой
стрелки. В противном случае тройка
называется левой.
Так, на рис. 1.16 тройка
является левой.
Рис. 1.16
Свойства ориентации
1. {
- правая}
{
- левая}.
2. {
- правая}
{
- левая}.
3. {
- правая}
{
- правая}.
Перестановка упорядоченного множества называется циклической, если каждый его элемент ставится на место предыдущего (или последующего). Как мы видим, при циклической перестановке тройки векторов ее ориентация не меняется.
Базисные векторы
правого ортонормированного базиса
будем обозначать
(так же, как и в школе). В дальнейшем мы
будем использовать только прямоугольные
системы координат, как правило, правые.
§ 3. Проекции
П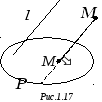
усть
в пространстве заданы плоскость
и прямая
,
не параллельная этой плоскости. Проекцией
произвольной точки
на плоскость
параллельно прямой
называется точка
пересечения плоскости
и прямой, проходящей через
параллельно
(рис. 1.17).
П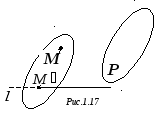
роекцией
произвольной точки
на прямую
параллельно плоскость
называется
точка
пересечения прямой
и плоскости, проходящей через
параллельно
(рис. 1.18). Проекцией множества точек на
плоскость (или на прямую) называется
множество проекций всех точек этого
множества на заданную плоскость (или
прямую). Если плоскость
и прямая
перпендикулярны, то проекции называются
ортогональными.
В дальнейшем мы будем рассматривать
только ортогональные проекции. В этом
случае проекция точки
на прямую совпадает с основанием
перпендикуляра, проведенного из точки
к этой прямой.
Пусть в пространстве
задана прямая
.
Если на ней выбрать направление с помощью
вектора
(
),
то прямая превратится в ось. Любой вектор
,
как и всякое множество, на эту ось можно
спроектировать. Полученный вектор будем
называть векторной проекцией вектора
на вектор
и обозначать
.
На рисунке 1.18
,
.
Алгебраической
проекцией
(или просто проекцией)
вектора
на
называется число
.
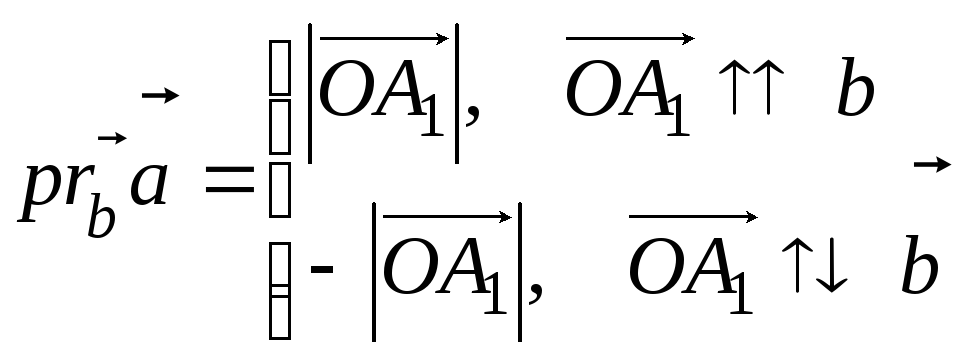Проекции обладают следующими свойствами.
1.
,
где
– угол между векторами
и
.
►
Если
острый угол, то (рис. 1.18)
;
если
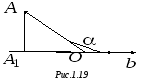
– тупой, то (рис. 1.19)
.
Если же
-
прямой угол, то
..◄
2.
,
т.е. проекция суммы векторов равна сумме
их проекций.
►Выберем в
пространстве ортонормированный базис
так, чтобы
.
Если в этом базисе вектор
имеет координаты
,
то, нетрудно убедиться, что
(рис. 1.20).Тогда доказываемое свойство
вытекает из свойств координат векторов.◄
3.
,
т.е. при умножении вектора на число его
проекция умножается на это число.
Это свойство также вытекает из свойств координат векторов.
§ 4. Преобразования систем координат на плоскости
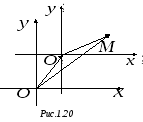
Параллельный
перенос. Параллельным
переносом называется
такое преобразование системы координат,
при котором координатные оси «старой»
и «новой» систем сонаправлены (рис.1.20).
Выберем на плоскости произвольную точку
и обозначим
ее координаты в старой системе и
– в новой.
Пусть начало новой системы координат
– точка
– в старой системе имеет координаты
.
На рис. 1.17
,
значит,
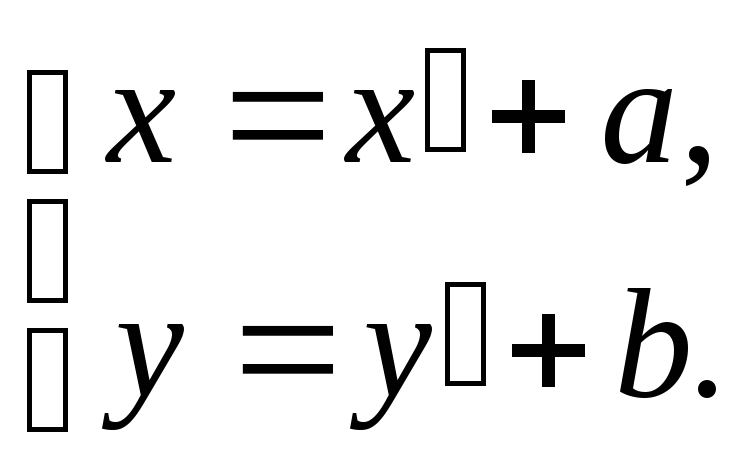(7)
Ф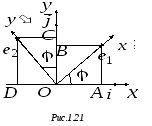
ормулы
(7) и задают преобразование параллельного
переноса.
Преобразование
поворота.
При повороте системы координат начала
старой и новой систем совпадают, а
базисные векторы новой образуют с
базисными векторами старой некоторый
угол
.
Обозначим векторы старой системы, как
обычно,
и
,
а векторы новой –
и
(длины всех базисных векторов равны
единице). На рис. 1.21 видим:
,
.
Если
– произвольная
точка плоскости,
и
– ее
координаты соответственно в старой и
новой
системах координат, то
,
откуда, учитывая единственность координат в выбранном базисе, получаем
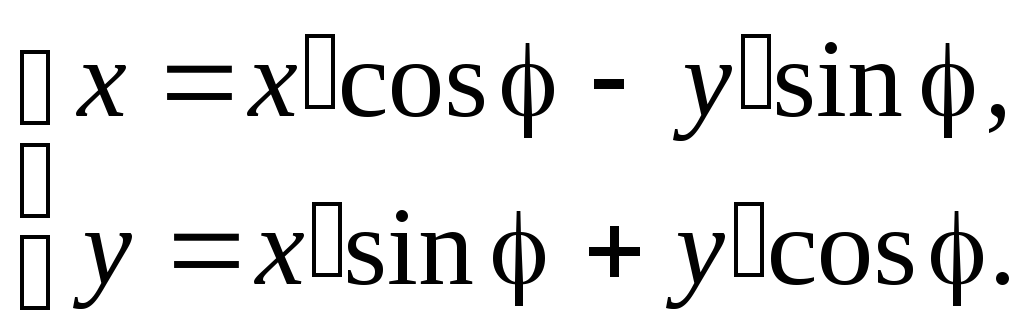(8)
Формулы (8) задают связь старых и новых координат точки при преобразовании поворота.