§ 2. Аффинная система координат

Базисом на прямой называется любой ненулевой вектор на этой прямой.

Теорема. Если на прямой задан базис , то для любого вектора на этой прямой существует число такое, что .

Доказательство вытекает из теоремы 1 §1.

Базисом на плоскости называется упорядоченная пара неколлинеарных векторов, принадлежащих этой плоскости.

Теорема. Если на плоскости задан базис , то для любого вектора на этой плоскости существует упорядоченная пара чисел такая, что .

Доказательство вытекает из теоремы 2 §1.

Базисом в пространстве называется упорядоченная тройка некомпланарных векторов.

Теорема. Если в пространстве задан базис

, (1)

то для любого вектора существует упорядоченная тройка чисел такая, что

. (2)

Р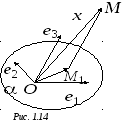 авенство (2) называется разложением вектора по базису (1), а коэффициенты разложения – координатами вектора в базисе (1).

►Выберем в пространстве некоторую точку О и отложим все векторы от этой точки. Обозначим плоскость, проходящую через точку О параллельно векторам и . Через конец вектора (точку М) проведем прямую, параллельную вектору , а точку пересечения её с плоскостью обозначим (см. рис. 1.14). Тогда

, (3)

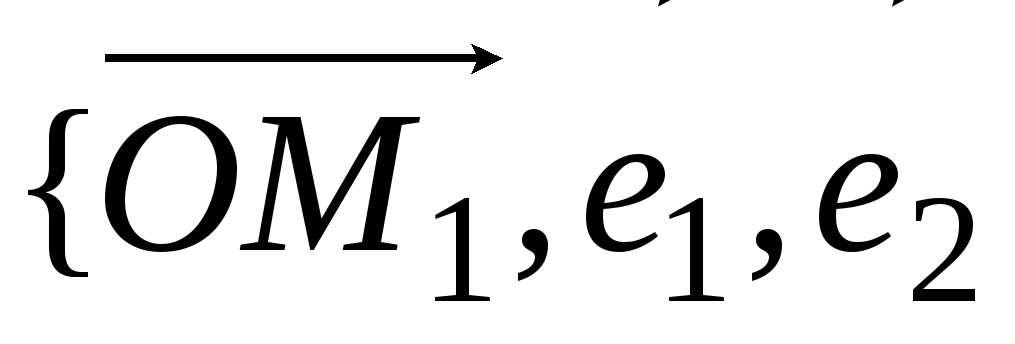- компланарны, и - неколлинеарны} [Т-2 §1]

, (4)

{} [Т-1 §1] . (5)

Теперь равенство (2) вытекает из (3), (4), и (5).◄

Свойства координат векторов

1. Координаты нулевого вектора в любом из базисов равны нулю.

2. Координаты вектора в данном базисе определяются однозначно.

3. При сложении векторов их соответствующие координаты складываются.

4. При умножении вектора на число все его координаты умножаются на это число.

5. Координаты линейной комбинации векторов равны таким же линейным комбинациям соответствующих координат слагаемых.

Эти свойства кажутся вам естественными, а мы докажем их позже.

Системой координат называется совокупность точки О, которая называется началом координат, и базиса.

Е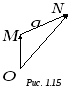 сли в пространстве задана система координат , то каждой точке можно поставить в соответствие вектор , который называется её радиус-вектором.

Координатами точки в выбранной системе координат называются координаты её радиус-вектора в соответствующем базисе.

Пусть при откладывании некоторого вектора от точки получается точка (рис. 1.15). Тогда вектор обозначается , а операция откладывания вектора от точки записывается следующим равенством:

Error: Reference source not found. (6)

Так как

(7)

и т.к. координаты точки совпадают с координатами её радиус-вектора, то из (6) получается правило: чтобы найти координаты конца вектора следует к координатам вектора прибавить соответствующие координаты его начала. Равенство (7) также равносильно равенству , из которого получаем: чтобы найти координаты вектора, следует из координат его конца вычесть соответствующие координаты начала.

Введенная система координат называется аффинной. Если базисные векторы попарно ортогональны, а длины их равны единице, то базис называется ортонормированным, а система координат – прямоугольной декартовой.