Умножение вектора на число
Определение.
Произведением вектора
на число
называется вектор
,
удовлетворяющий
следующим условиям:
-
; -
,
.
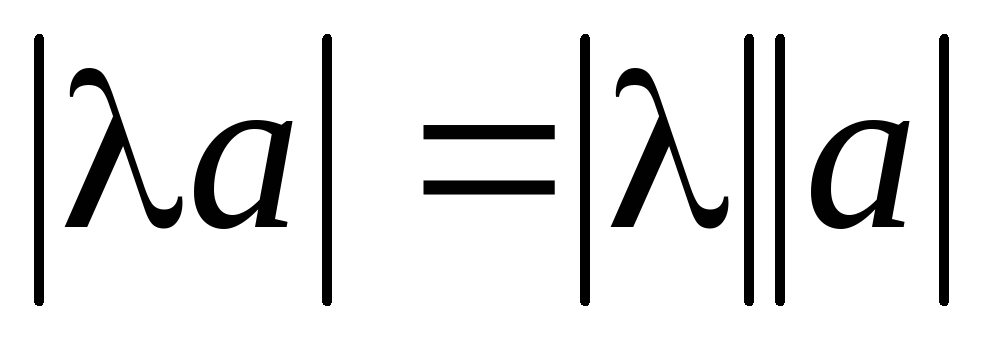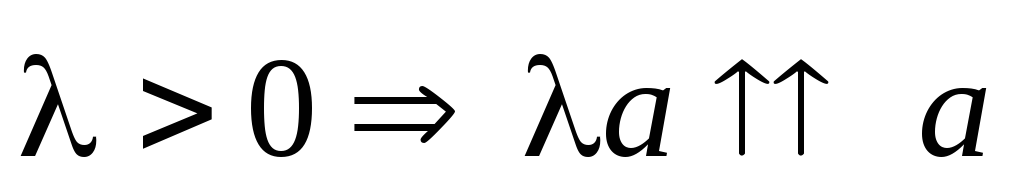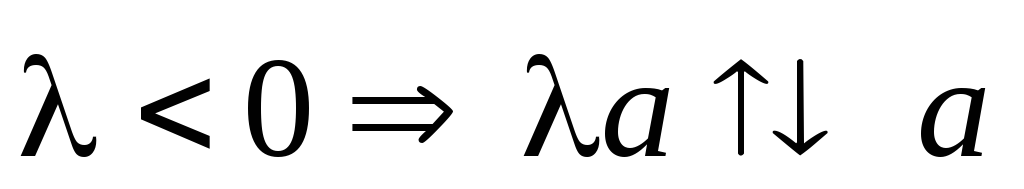Следствия.
1.
.
►
.◄
2.
.►
.◄
3.
.►
◄
► ◄
Свойства операции умножения вектора на число
-
:
; -
:
; -
:
; -
:
; -
:
.
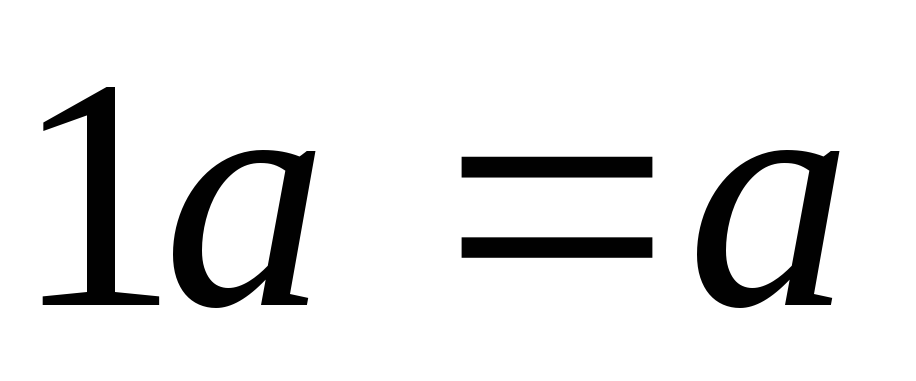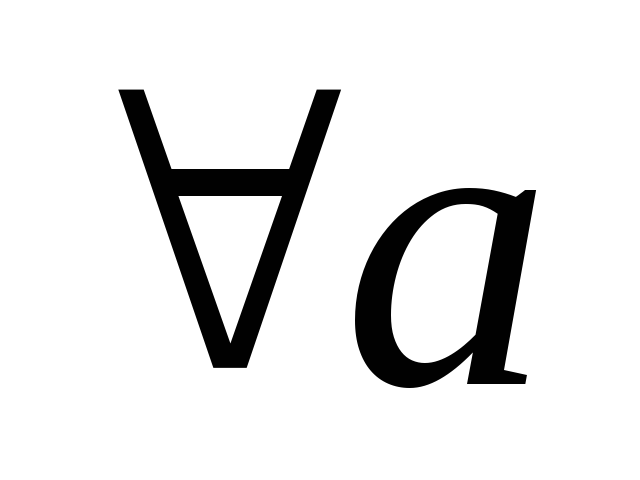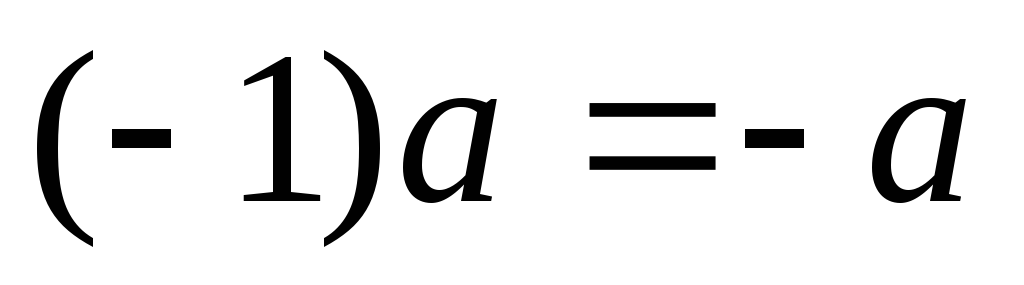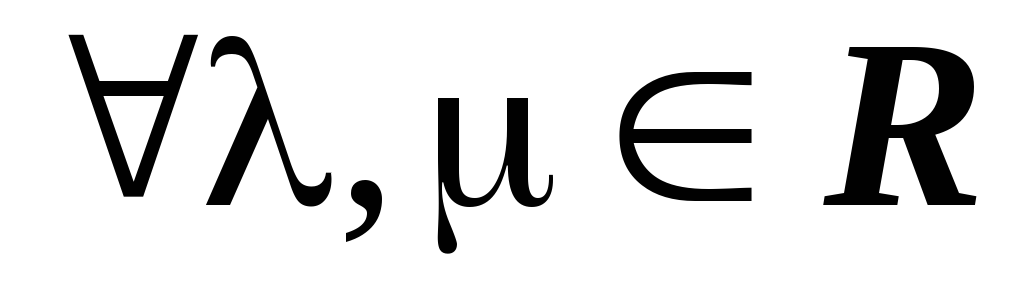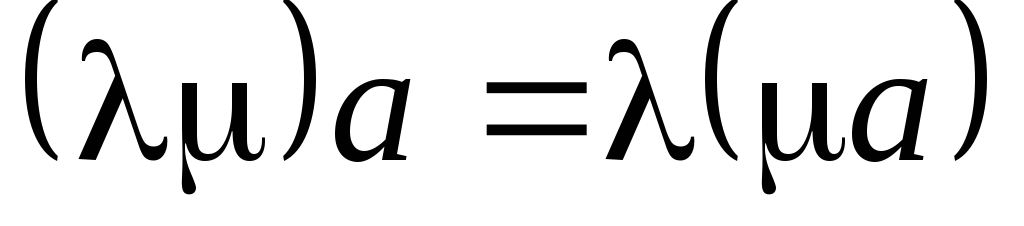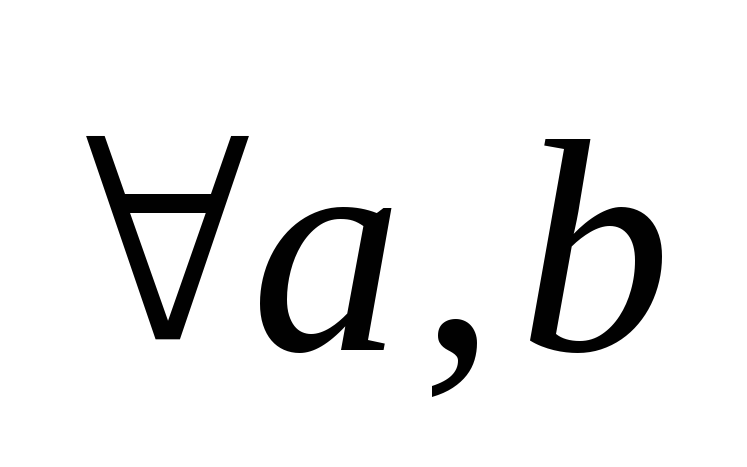
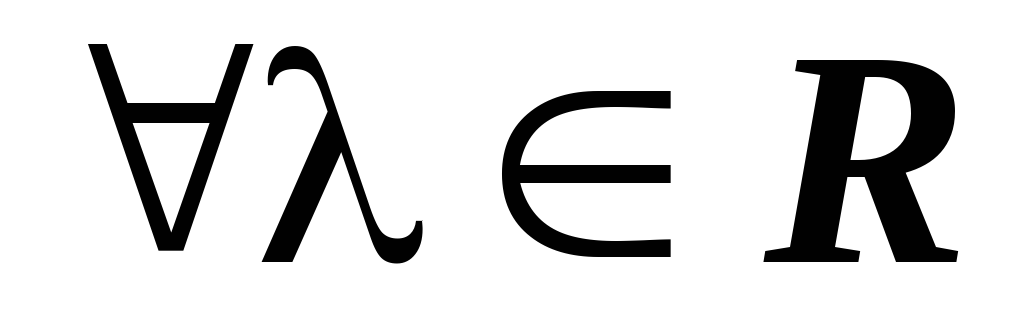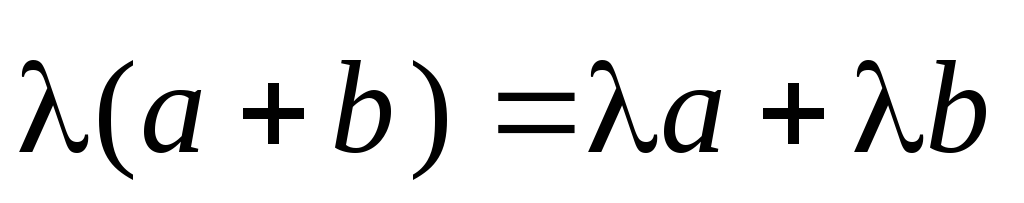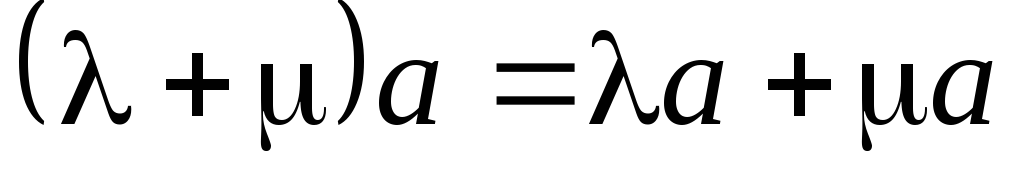Первое из приведенных свойств, очевидно, выполняется, докажем остальные.
2.
►
,
,
значит, векторы
и
противоположны.◄
3. ► Если одно
из чисел
или
равно нулю, либо вектор
– нулевой, то равенство верно. В любом
случае длины векторов в левой и правой
частях совпадают, так как
и
.
Остается доказать совпадение их
направлений. Если
и
,
рассмотрим несколько случаев.
а)
.
Тогда
;
.
Таким образом, векторы в левой и правой
частях равенства сонаправлены одному
и тому же ненулевому вектору, поэтому
они также сонаправлены.
б)
.
Тогда
;
,
и опять векторы сонаправлены.
в)
.
Тогда
;
.
Векторы в левой и правой частях равенства
противонаправлены одному и тому же
ненулевому вектору, поэтому они
сонаправлены.
г)
.
Случай, аналогичный предыдущему.◄
4
.
►При
или
равенство, очевидно, выполняется.
Рассмотрим остальные случаи.
а)
,
,
векторы
и
неколлинеарны. От произвольной точки
отложим векторы
и
,
а от точки
– вектор
.
Проведем прямую через точки
и
,
а через точку
– прямую, параллельную
.
Точку пересечения построенных прямых
обозначим
(рис.1.6). Из подобия треугольников
и
вытекает:
,
,
значит
;
,
,
значит
.
Тогда
.
С другой стороны,
,
откуда и вытекает доказываемое равенство.
б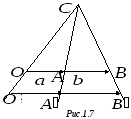
)
,
,
векторы
и
коллинеарны. От произвольной точки
отложим векторы
,
от точки
– вектор
.
Выберем произвольную точку
,
проведем через нее прямые
,
,
и на прямой
отложим отрезок
(рис. 1.7). Через точку
проведем прямую, параллельную
,
и обозначим точки ее пересечения с
прямыми
и
соответственно
и
.
Из подобия треугольников
и
вытекает, что
,
,
значит,
.
Аналогично из подобия треугольников
и
получаем, что
,
а из подобия треугольников
и
– что
.
С другой стороны,
,
откуда и вытекает доказываемое равенство.
в)
.
Вектор
противоположен вектору
.
Но вектор
также противоположен
,
так как
,
поэтому
.
г)
.
Тогда
◄
5. ►а)
.
Равенство, очевидно, выполняется.
б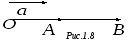
)
.
Тогда
.
Но и
,
поэтому
,
значит
.
Остается доказать равенство длин. На
рисунке 1.8.
.
По рисунку видно, что
.
С другой стороны,
.
в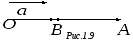
)
.
Тогда
,
.
На рисунке 1.9.
.
По рисунку видно, что
.
Кроме того
.
С другой стороны,
,
поэтому
и
.
Аналогично равенство
доказывается в случае, когда
.◄
Критерии коллинеарности и компланарности
Теорема 1
(критерий коллинеарности).
Для того чтобы векторы
и
были коллинеарными, необходимо и
достаточно, чтобы один из них можно было
представить в виде произведения другого
вектора на число, т.е., чтобы существовало
число
такое, что
,
или существовало бы число
такое, что
.
При этом, если один из векторов ненулевой,
то второй можно через него выразить.
►Достаточность.
Дано:
.
Тогда
согласно определению произведения
вектора на число.
Необходимость.
Дано:
.
Рассмотрим два случая:
-
Один из векторов нулевой, например,
.
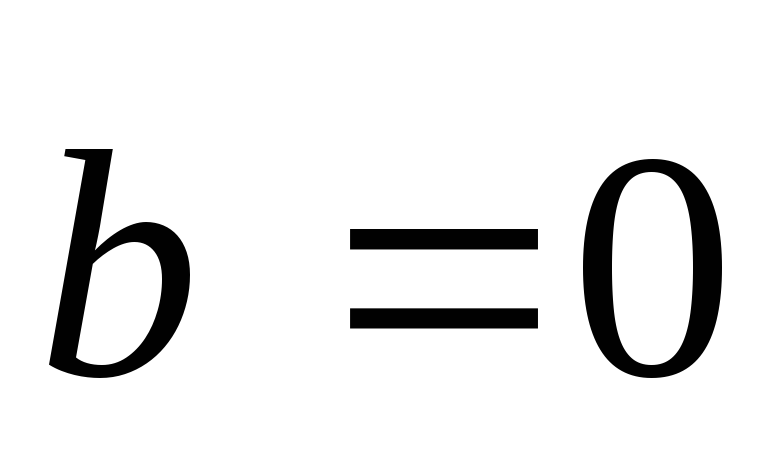Тогда
,
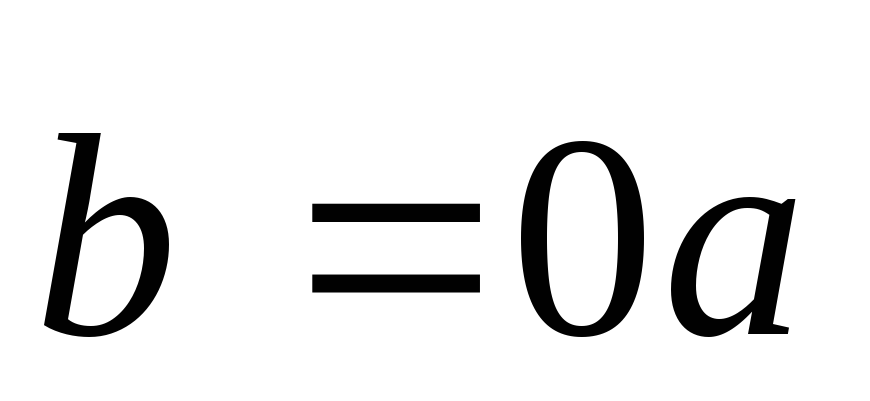т.е.
. -
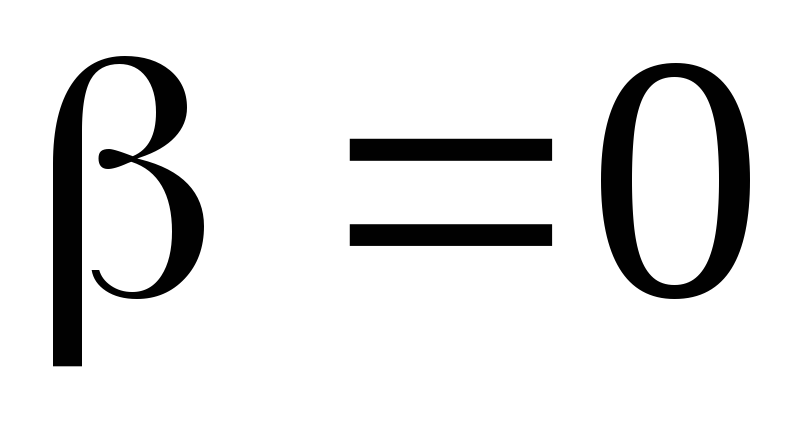Оба вектора ненулевые. Положим
.
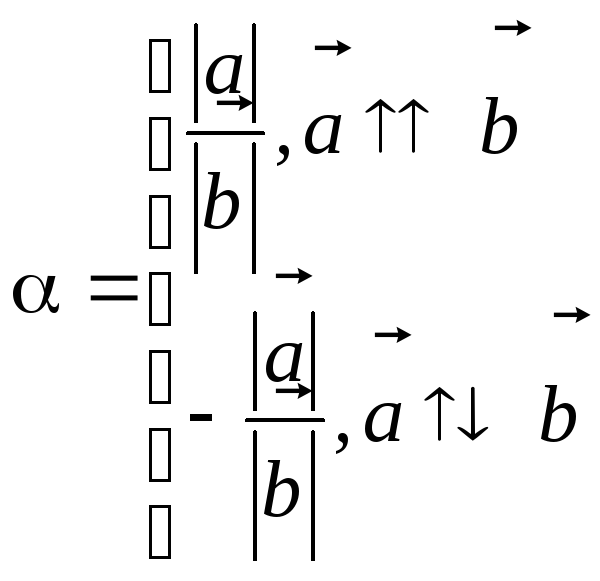Тогда
.
Кроме того,
(рис. 1.10);
(рис. 1.11).
Рис. 1.10 Рис.1. 11
Таким образом,
векторы
и
имеют одинаковые длину и направление,
значит, они совпадают.
Теорема 2 (критерий компланарности). Для того чтобы три вектора были компланарными, необходимо и достаточно, чтобы один из них можно было представить в виде линейной комбинации двух других. При этом если два из векторов неколлинеарные, то третий можно через них выразить.
►
Достаточность.
Дано: один
из векторов можно представить в виде
линейной комбинации двух других, например
.
Возможны два случая.
а)
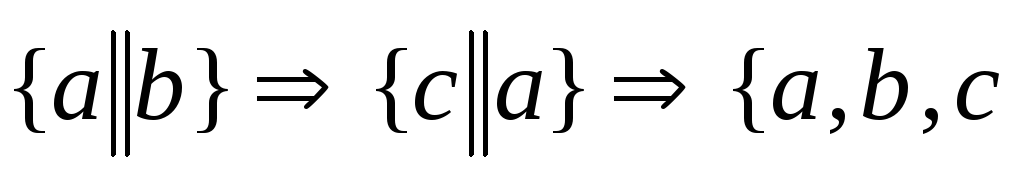- компланарны}.Error: Reference source not found
б) Векторы
и
неколлинеарные. Доказательство вытекает
из того, что треугольник – плоская
фигура (см. рис. 1.12).
Необходимость.
Дано:
- компланарны.
а)
;
б)
и
- неколлинеарные. Отложим все три вектора
от одной точки О
(см. рис 1.13) и проведем
Тогда:
,
Error: Reference source not found
(1)
,
(2)
,
(3)
Из (1), (2), (3) вытекает,
что
.◄