АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ И ЛИНЕЙНАЯ АЛГЕБРА

КУРС ЛЕКЦИЙ

ДЛЯ СТУДЕНТОВ

ФАКУЛЬТЕТА РАДИОФИЗИКИ И ЭЛЕКТРОНИКИ

ПРЕПОДАВАТЕЛЬ БЕРЁЗКИНА Л.Л.,

ДОЦЕНТ КАФЕДРЫ ВЫСШЕЙ МАТЕИАТИКИ И

МАТЕМАТИЧЕСКОЙ ФИЗИКИ БГУ

Л И Т Е Р А Т У Р А

1. Р.Ф.Апатёнок и др. Элементы линейной алгебры и аналитической

геометрии.

2. В.А. Ильин, Э.Г.Позняк. Аналитическая геометрия.

3. В.А.Ильин, Э.Г.Позняк. Линейная алгебра.

4. Д.В. Беклемишев. Курс аналитической геометрии и линейной алгебры.

5. Н.Г. Абрашина-Жадаева и др. Аналитическая геометрия в примерах и задачах.

6. А.А.Бурдун и др. Сборник задач по алгебре и геометрии.

Часть I. Аналитическая геометрия глава 1. Элементы векторной алгебры

§ 1. Векторы и линейные операции над ними

Понятие вектора

Связанным вектором называется направленный отрезок. Связанный вектор характеризуется длиной, направлением и точкой приложения. Примером связанного вектора может служить сила, приложенная к упругому телу.

Направленные отрезки называются эквивалентными, если они имеют одинаковые длины и направления. направленному отрезку , называется множество всех направленных отрезков

Свободным вектором, соответствующим, эквивалентных (рис 1.1). Этот свободный вектор будем обозначать . Если направленные

Рис. 1.1 отрезки и эквивалентны, то по определению =. Свободные векторы также обозначаются малыми латинскими буквами со стрелками, например, . Свободный вектор характеризуется только длиной и направлением (примером может служить угловая скорость). Каждый направленный отрезок, принадлежащий данному свободному вектору, называется его представителем. На рисунке свободные векторы изображаются своими представителями. Если свободный вектор изображен своим представителем ,то говорят, что вектор отложен от точки . Операцию откладывания вектора от точки удобно записывать следующей формулой: .

В аналитической геометрии, как правило, используются свободные векторы. Слова «свободный» и «связанный» обычно опускаются, о каких векторах идет речь должно быть понятно из контекста. Обозначать связанные и свободные векторы также будем одинаковым образом.

Свободные векторы называются коллинеарными, если их представители параллельны одной и той же прямой.

Свободные векторы называются компланарными, если их представители параллельны одной и той же плоскости.

Нулевым называется свободный вектор, у каждого представителя которого начало совпадает с концом. Нулевой вектор не имеет направления, по определению считается, что нулевой вектор сонаправлен любому вектору, а также и перпендикулярен любому вектору.

Длиной свободного вектора называется длина любого из его представителей. Длина нулевого вектора равна нулю.

Углом между свободными векторами называется угол между его представителями, отложенными от одной точки.

Сложение векторов

Определение. Error: Reference source not foundПусть заданы свободные векторы и . Выберем в пространстве произвольную точку О и отложим от неё вектор . Получим направленный отрезок

. От точки А отложим вектор . Получим направленный отрезок .Error: Reference source not found Свободный вектор, представителем которого является направленный отрезок , называется суммой свободных векторов и (рис. 1.2).

У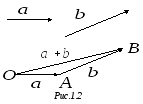 пражнение.Докажите корректность определения, т.е. докажите, что результат сложения не зависит от выбора точки О.

Приведенное правило сложения векторов называется правилом треугольника или правилом замыкающей.

Свойства операции сложения

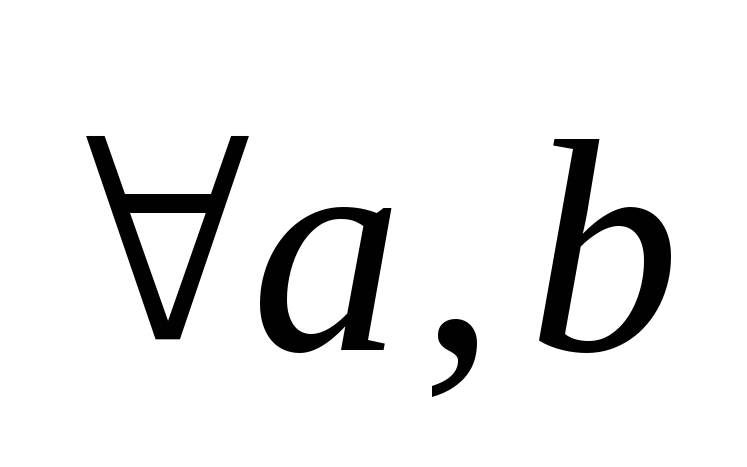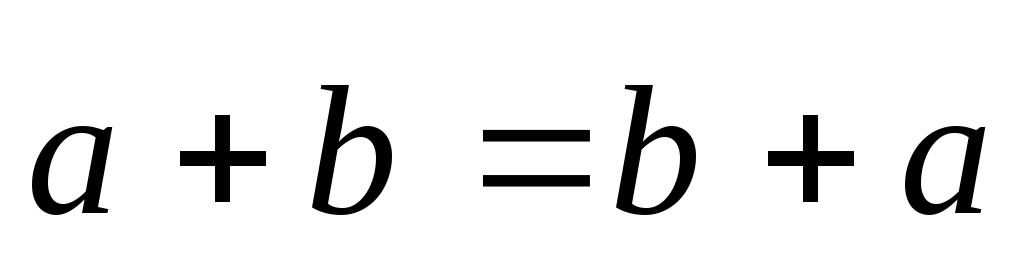1. : (коммутативность);

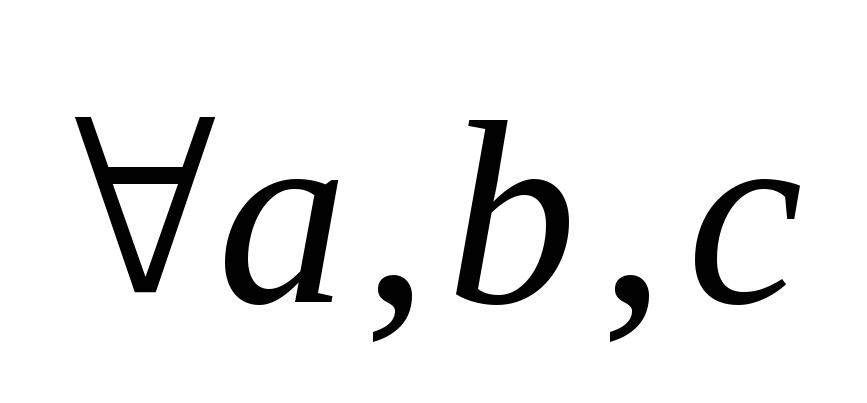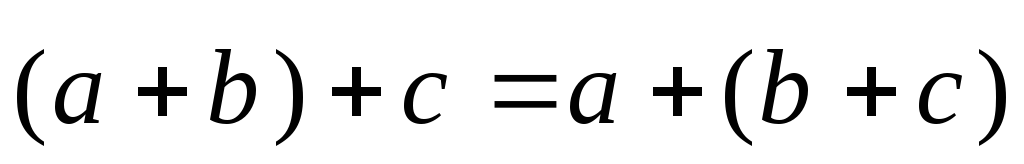2. : (ассоциативность);

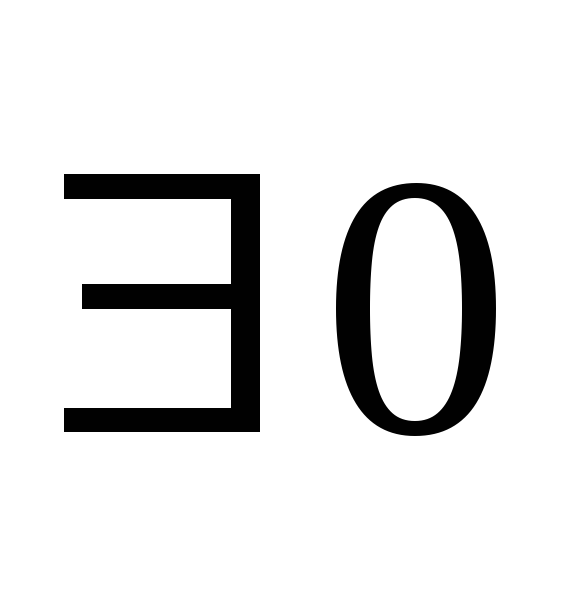
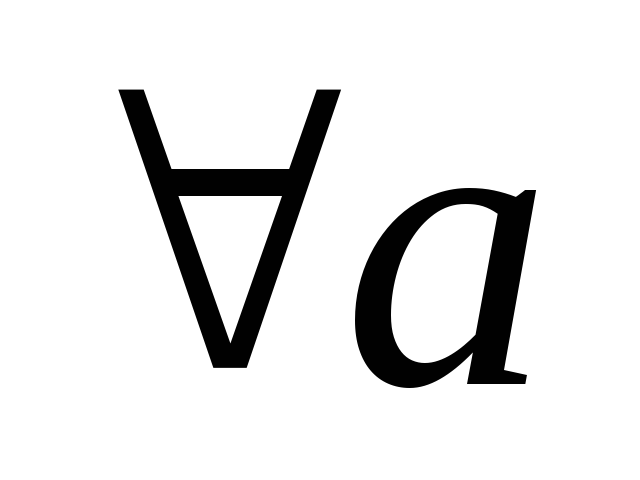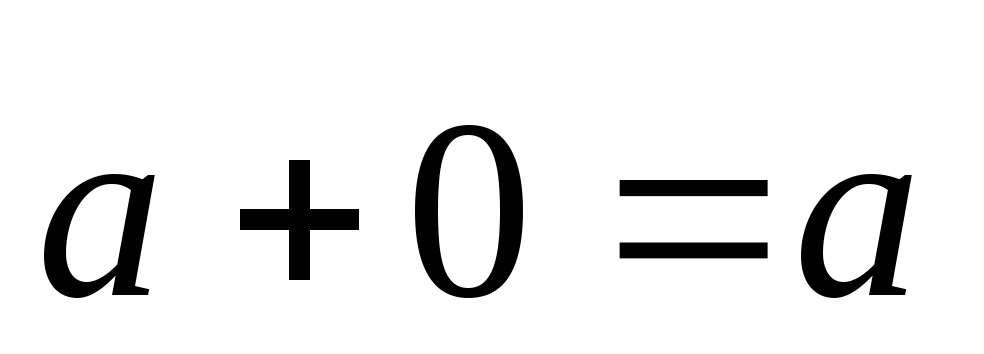3. : (существование нейтрального элемента);

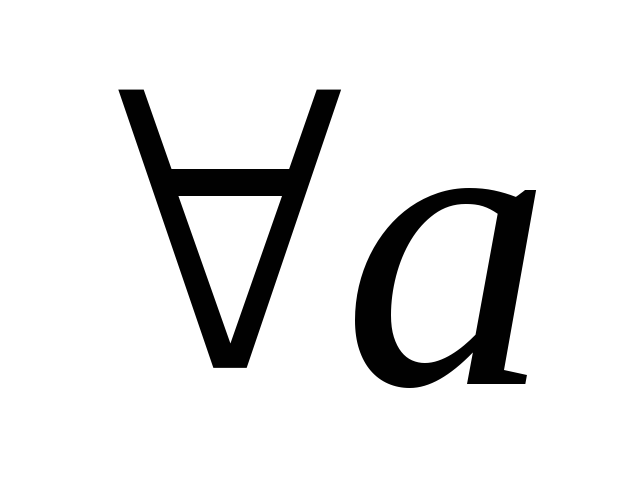
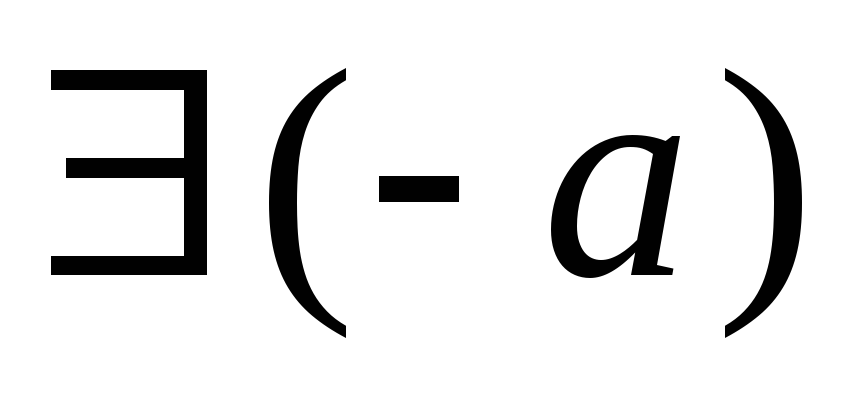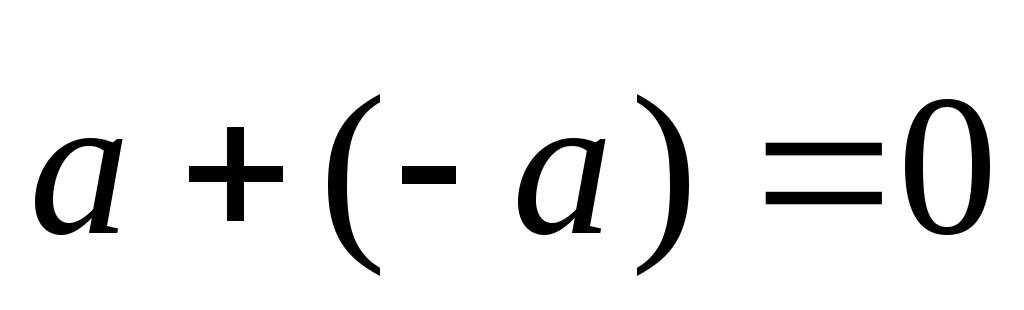4. : (существование противоположного элемента).

П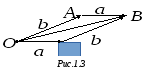 риведем их доказательства.

1 .►а) Векторы и неколлинеарны. От произвольной точки пространства отложим вектор , от точки отложим вектор и достроим полученную фигуру до параллелограмма (рис.1.3). Так как в параллелограмме противоположные стороны равны и параллельны, то , . На рисунке 1.3 видно, что , , откуда и получается доказываемое равенство. Из этого доказательства вытекает еще одно правило сложения двух неколлинеарных векторов: правило параллелограмма.

б) Доказательство для коллинеарных векторов легко получается из правила замыкающей (рис. 1.4).◄

2.►На рис. 1.5 , , ; ; , откуда и вытекает доказываемое равенство.◄

И з свойства ассоциативности получаем: так как неважно, где поставить скобки при сложении трех векторов, их можно не ставить вообще (так же, как и при сложении чисел). Таким образом, определяется сумма трех и более векторов.

3.► Нейтральным элементом, очевидно, является нулевой вектор.◄

4.► Если , положим . Очевидно, что .◄

Во множестве векторов можно ввести и операцию вычитания следующим образом: по определению положим .