4.3. Проверка гипотезы соответствия эмпирической и теоретической

функций распределения

В настоящее время известно большое число самых разнообразных тестов на проверку соответствия экспериментальных данных заданной теоретической функции распределения. В общем случае такая проверка может быть выполнена с помощью как упрощенных, так и более строгих методов. Приближенные способы позволяют производить быструю проверку с помощью относительно простых тестов (критериев). Более строго это можно осуществить на основе критериев согласия. Критериями согласия принято называть статистические критерии, предназначенные для проверки соответствия между гипотетической теоретической моделью и реальными данными, которые эта модель должна описать. Другими словами, они выясняют, насколько предположения о распределении случайных величин соответствуют экспериментальным данным, т.е. не вступает ли принятая теоретическая модель в противоречие с исходными данными. Учитывая, что такой теоретической моделью для случайной выборки служит закон распределения, критерии согласия прежде всего применяются для проверки соответствия эмпирической и теоретической функций распределения.

Критериями согласия являются статистики Пирсона ², Колмогорова–Смирнова, Мизеса–Крамера ². Рассмотрим наиболее широко используемые в практических расчетах первые два критерия.

Критерий Пирсона ². Данный критерий является непараметрическим и используется для выборок достаточно большого объема при проверке любых теоретических функций распределения, которые должны быть заданы в дифференциальном виде. Предварительно осуществляется ранжирование ряда и разбиение его на градации. Считается, что длина выборки должна быть n≥50, причем число градаций должно быть не меньше 5, а в каждой из градаций число должно быть минимум 5–7 наблюдений. Последнее требование на практике обычно очень сложно выполнить, так как «хвосты» (края) эмпирического распределения имеют значительно более низкую повторяемость по сравнению с его центральной частью.

Прежде всего, формулируется нулевая гипотеза. Например, соответствие эмпирической функции распределения с параметрамих, s2 нормальному закону с параметрами mх, Dx может быть записано как

Н₀ : f(х, s²) = f(m_х, D_x).

Альтернативную гипотезу зададим в обычном виде н1 : f(х, s2)  f(mх, Dx). В качестве меры расхождения между эмпирическими данными и теоретической функцией распределения используется выражение:

_{k k}

² = n(р_i – p_i)²/p_i = (m_i – np_i)²/np_i, (4.4)

^{i=1 i=1}

где р_i - эмпирическая вероятность в i-й градации; р_i – теоретическая вероятность; k – число градаций в выборке объемом n; m_i – абсолютная эмпирическая частота (число событий) в i-й градации.

После того как на основе эмпирических данных по формуле (4.4) вычисляется величина ², осуществляется проверка неравенства ²>²_кр(,) (приложение 2). При этом число степеней свободы определяется как  = kξ1, где ξ – число параметров теоретического распределения. Поскольку для нормального закона ξ = 2, то имеем = k3. Если данное неравенство выполняется, то нулевая гипотеза о соответствии эмпирического распределения нормальному закону отвергается. Если ²<²_кр(,), то у нас уже нет оснований отвергать нулевую гипотезу о нормальном распределении генеральной совокупности. В связи с этим можно полагать, что расхождения между эмпирическими и теоретическими частотами являются незначимыми, т.е. носят случайный характер.

Следует иметь в виду, что градации с малым числом событий (m<5) целесообразно объединять вместе. Естественно, в этом случае величина k определяется по числу окончательных градаций.

Критерий Колмогорова–Смирнова. Данный критерий также может быть использован для проверки любой теоретической функции распределения. В отличие от критерия Пирсона его удобнее использовать для интегральных функций распределения. Нулевая гипотеза записывается аналогично предшествующему случаю. Проверка ее осуществляется с помощью статистики D, представляющей собой модуль максимального уклонения между эмпирической F(x) и теоретической F(x) функциями распределения, т.е.

D = max | F(x) – F(x)|. (4.5)

^{х(-,)}

Статистика D является случайной величиной, предельное распределение которой было установлено Колмогоровым. Оно выражает вероятность того, что при неограниченном возрастании объема выборки значение D не будет превосходить заданного числа ₀:

.

В практических расчетах более удобно пользоваться величиной , которая может быть вычислена как

 = Dn^1/2. (4.6 )

Оценка величины D как максимального уклонения между F(x) и F(x) демонстрируется на рис. 4.2. Значения статистики _кр, зависящие лишь от уровня значимости, затабулированы и приводятся в табл. 4.3.

Таблица 4.3

Распределение статистики _кр в зависимости от уровня значимости 

Уровень значимости	0,30	0,20	0,10	0,05	0,025	0,01	0,005	0,001
Критическое значение кр	0,97	1,07	1,22	1,36	1,48	1,63	1,73	1,95

Главное условие к исходной информации – непрерывность. Поскольку на практике мы имеем дело обычно с дискретными данными, то вариационный (ранжированный) ряд должен быть предварительно сгруппирован по очень малым градациям, чтобы различия между ними были как можно меньше. В принципе статистика  может быть вычислена и непосредственно по индивидуальным (несгруппированным) значениям, однако в этом случае к выводам, получаемым с помощью критерия Колмогорова–Смирнова, следует относиться с максимальной осторожностью.

Итак, общая последовательность проверки гипотезы о законе распределения заключается в следующем:

1. Строятся эмпирическая функция распределения F(x) и предполагаемая теоретическая функция F(x).

2. Определяется статистика D и вычисляется величина .

3. Если выполняется неравенство  > _кр(α), то нулевая гипотеза о том, что случайная величина Х соответствует заданному теоретическому закону распределения отвергается. В противном случае у нас нет оснований отвергать нулевую гипотезу и, следовательно, она не противоречит тому, что опытные данные распределяются по заданному закону распределения.

Следует иметь в виду, что при использовании данного критерия учитывается лишь наибольшее уклонение эмпирических данных от принятой теоретической функции распределения. Поэтому он использует далеко не всю информацию, заключающуюся в исходной выборке. Действительно, нетрудно представить себе, что эмпирические данные систематически уклоняются от принятой теоретической кривой в разные стороны, но не настолько, чтобы повысить максимальное уклонение, т. е. величину D. В этих случаях критерий Колмогорова будет показывать на хорошее согласие теоретической и эмпирической функций распределения.

Если к этой же выборке применить критерий Пирсона, то в соответствии с ним будет осуществляться суммирование квадратов уклонений для каждой из градаций. Поскольку сумма может оказаться весьма значительной и превысить критическое значение критерия, то эмпирическая функция распределения будет уже не соответствовать теоретической.

Итак, при использовании критериев согласия получаем противоположные выводы. Какой же из них более верный? На наш взгляд, более точным при проверке данной нулевой гипотезы следует считать критерий ², так как он использует практически всю информацию, содержащуюся с исходной выборке.

Пример 4.3. Как было показано в примере 3.2, эмпирическое распределение поверхностной температуры воды на гидрологической станции в Белом море в летний период является близким к симметричному. Учитывая важность нормального закона распределения для статистического анализа, выполним оценку степени соответствия исходных данных указанному теоретическому закону на основе критериев согласия Пирсона и Колмогорова. Предварительный анализ значений температуры воды, разбитых на 8 градаций (интервалов), был ранее представлен в табл. 3.1, поэтому воспользуемся оценками эмпирической частоты, которые перенесем в табл. 4.4.

Далее по формуле f(x) = 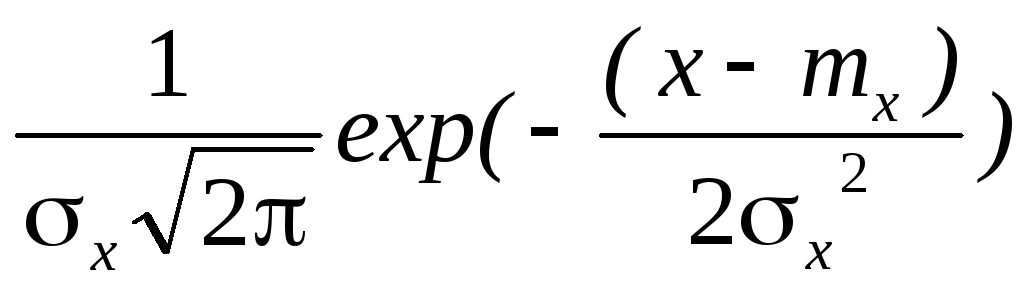рассчитываем теоретические оценки вероятности нормальной функции распределения для середин интервалов (табл.4.4). Отметим, что в качестве m_x и _x берутся выборочные оценки среднего арифметического и стандартного отклонения (x = 11,9 ^oC, s = 0,9 ^оС.).

Таблица 4.4

Проверка соответствия эмпирических данных нормальному закону распределения по критерию Пирсона

Номер градации	Градация, оС	Эмпирическая частота, mi	Вероятность, pi	Теоретическая частота, npi	(mi-npi)2	(mi-npi)2/npi
1	9,4-10,0	3 (10)	0,017	1,7 (7,6)	5,76	0,758
2	10,0-10,6	7	0,059	5,9
3	10,6-11,2	11	0,141	14,1	9,61	0,682
4	11,2-11,8	20	0,228	22,8	7,84	0,344
5	11,8-12,4	28	0,247	24,7	10,89	0,441
6	12,4-13,0	19	0,182	18,2	0,64	0,035
7	13,0-13,6	10	0,087	8,7	0,16	0,014
8	13,6-14,2	2 (12)	0,029	2,9 (11,6)
		100	0,990	99,0		2,27

Так как эмпирические частоты первого и последнего интервалов малы (меньше 5), то для получения более достоверных результатов целесообразно при использовании критерия Пирсона объединить указанные градации с соседними. Эти оценки приведены в табл. 4.4 в скобках. Итак, теперь уже нетрудно рассчитать статистику ², которая дана в последней графе ²=2,27. Далее осуществляется проверка неравенства ²>²_кр(,), причем число степеней свободы  = k – 3 = 6 – 3 = 3. Принимая уровень значимости  = 0,05, находим по распределению Пирсона ²_кр = 7,82. Нетрудно видеть, что ² < ²_кр. Следовательно, у нас нет оснований отвергать нулевую гипотезу о нормальном распределении генеральной совокупности. Можно полагать, что гипотеза о выбранном нормальном распределении согласуется с опытными данными, а расхождения между эмпирическими и теоретическими частотами носят случайный характер.

Теперь подвергнем проверке нулевую гипотезу о соответствии эмпирической функции распределения нормальному закону с помощью критерия Колмогорова. С этой целью пересчитаем дифференциальную эмпирическую функцию f(x) в интегральную функцию F(x). Эмпирические оценки функции F(x), которые соответствуют накопленной частости (см. табл. 3.1), приведены в табл. 4.5.

Далее следует рассчитать теоретические оценки F(x). Для этого можно воспользоваться, например, формулой (3.4)

F(x) = 0,5 + 0,5Ф[(х – m_x)/_x].

Исходя из этой формулы, для первого значения ПТВ получим

F(9,4) = 0,5 + 0,5Ф[9,4 11,9)/0,93] = 0,5+0,5Ф(2,69) = 0,50,50,9928  0,004.

Таблица 4.5

Сравнение эмпирической и теоретической (нормальной) функций распределения для температуры воды на гидрологической станции в Белом море

x	9,4	10,0	10,6	11,2	11,8	12,4	13,0	13,6	14,2
F(x)	0,010	0,030	0,100	0,210	0,410	0,690	0,880	0,980	1,000
F(x)	0,004	0,021	0,080	0,221	0.449	0,695	0,878	0,964	0,993

Аналогичным образом рассчитываются все остальные оценки функции F(x). Сравнение значений эмпирической и теоретической функций распределения, указанных в табл. 4.5, показывает, что максимальное расхождение между ними отмечается при температуре Т=11,8 ^оС. Величина D=|0,410-0,449| = 0,039. Вычислим  = D(n)^1/2 = 0,039(100)^1/2 = 0,39. Так как <_кр при любом числе степеней свободы, то можно полагать, что нулевая гипотеза о выбранном нормальном распределении согласуется с опытными данными.