4.2. Проверка гипотез о равенстве выборочных средних и дисперсий

Одним из важнейших понятий случайного процесса является стационарность, под которой, как будет указано в разд. 9, приближенно можно понимать постоянство во времени выборочных средних и дисперсии. Понятие стационарности является одним из ключевых при анализе случайных процессов. Одним из простейших способов проверки стационарности является использование статистических гипотез о равенстве выборочных средних и дисперсий, причем проверку нужно начинать с равенства дисперсий. При этом не обязательно выборку делить пополам или на несколько равных частей. Впрочем, проверка этих гипотез широко применяется при решении многих других задач. Критериями для их проверки служат параметрические критерии Стьюдента и Фишера.

Гипотеза о равенстве средних при неизвестных генеральных дисперсиях.

Рассмотрим две независимые выборки X и Y, объемы которых равны m и n соответственно, причем известно, что они извлечены из нормальных генеральных совокупностей, имеющих равные дисперсии (D_x=D_y=D). При этом сами генеральные (истинные) дисперсии, а также математические ожидания m_x и m_y неизвестны. Прежде всего сформулируем нулевую гипотезу о равенстве средних значений этих выборок, т.е. Н₀ :х =y. Альтернативную гипотезу примем в виде Н₁ :х y.

Поскольку указанные выборочные средние имеют нормальное распределение, то естественно считать, что их разность также должна быть распределена по нормальному закону. В этом случае для проверки нулевой гипотезы может быть использована статистика Стьюдента, рассчитываемая по следующей формуле

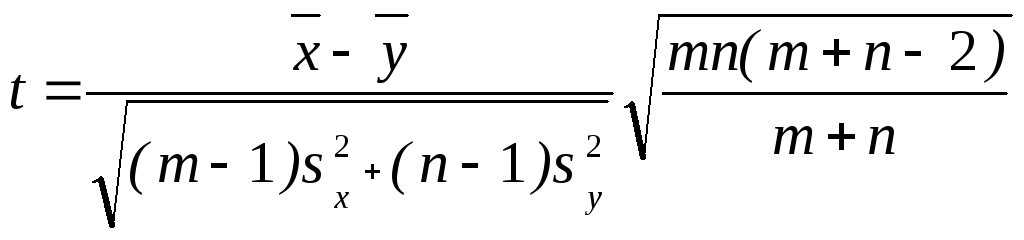, (4.1)

где s²_х и s²_y – выборочные оценки дисперсий первой и второй совокупностей, m и n - соответственно длина первой и второй выборки. Как известно, статистика t распределена по закону Стьюдента с =n+m2 степенями свободы (приложение 3).

После этого осуществляется проверка неравенства t > t_кр(,), где t_кр(,) – критическое значение статистики Стьюдента, соответствующее уровню значимости  и числу степеней свободы =n+m2. Если данное соотношение выполняется, то нулевая гипотеза о равенстве средних значений отвергается и можно сделать вывод, что выборочные средние, извлеченные из нормальных генеральных совокупностей, имеют значимые расхождения (не равны друг другу) при заданном уровне значимости. В противоположном случае, т.е.

t < t_кр у нас есть основания считать, что расхождения между выборочными средними не являются значимыми.

Гипотеза о равенстве средних при известных генеральных дисперсиях.

Нулевая гипотеза формулируется аналогичным образом, причем, если известны дисперсии генеральных совокупностей, то проверить ее гораздо легче. Для этого необходимо вычислить критерий

Z = |x y| / (D_x/m + D_y/n)^1/2, (4.2)

где D_x и D_y – генеральные дисперсии двух выборок. Затем по таблице функции Лапласа находится критическая точка Z_кр из равенства

Ф(Z_кр) = (1  )/2.

Если выполняется неравенство Z > Z_кр, то нулевая гипотеза о равенстве средних отвергается, если Z < Z_кр, то у нас нет оснований отвергать нулевую гипотезу.

Заметим, что указанные критерии являются точными и могут быть использованы как для больших, так и для малых выборок, извлеченных из нормальных генеральных совокупностей. С известной долей осторожности они могут быть использованы в тех случаях, когда D_xD_y, а также для больших выборок с неизвестным законом распределения, ибо в соответствии с центральной предельной теоремой величины x иy распределены асимптотически нормально. Отметим, что генеральные дисперсии известны редко, поэтому данный критерий не нашел широкого применения.

Гипотеза о равенстве дисперсий при неизвестных средних.

Рассмотрим опять две независимые выборки X и Y, объемы которых равны m и n соответственно. Эти выборки извлечены из нормальных генеральных совокупностей, причем математические ожидания их неизвестны. Требуется проверить равенство выборочных дисперсий. Для этого составляем нулевую гипотезу вида Н₀ : s²_x = s²_y при альтернативе Н₁ : s²_x  s²_y. Наиболее точным критерием ее проверки, как известно, является статистика Фишера (дисперсионное отношение), определяемое по формуле

F = s²_x/s²_y, (4.3)

причем принимается, что s²_x>s²_y. Выборочные оценки s²_x и s²_y рассчитываются как

_{m n}

s²_x = (m 1)^-1(x_i x)², s²_y = (n  1)^-1(y_i y)²

^{i=1 i=1}

Далее осуществляется проверка неравенства F > F_кр(;₁,₂), где ₁ = n1 ₂ = m1 (приложение 4). Если оно выполняется, то нулевая гипотеза о равенстве выборочных дисперсий отвергается и можно сделать вывод, что выборочные дисперсии, извлеченные из нормальных генеральных совокупностей, имеют значимые расхождения (не равны друг другу) при заданном уровне значимости. Если оно не выполняется, то у нас нет оснований для отвержения нулевой гипотезы.

Гипотеза о равенстве дисперсий при известных средних.

Данная гипотеза проверяется аналогично предыдущей. Различие состоит в том, что при оценке выборочных дисперсий используются значения математических ожиданий m_х и m_y, т.е.

_{m n}

s²_x = m ^-1(x_i  m_x)², s²_y = n ^-1(y_i  m_y)².

^{i=1 i=1}

Заметим, что данная гипотеза проверяется очень редко, поскольку математические ожидания генеральных совокупностей за редким исключением неизвестны.

Гипотеза о равенстве нескольких дисперсий.

Для сравнения нескольких дисперсий нормальных генеральных совокупностей по выборкам одинакового объема может быть использован критерий Кочрена, а различного объема – критерий Бартлетта. Однако оба критерия обладают недостатками. Так, критерий Бартлетта является весьма приближенным, а распределение критерия Кочрена хотя известно точно, но он имеет существенно меньшую мощность, чем, например, критерий Фишера. Поэтому, на наш взгляд, для сравнения нескольких дисперсий все же целесообразно пользоваться критерием Фишера. С этой целью осуществляется ранжирование величин дисперсий и затем производится сравнение наибольшей и наименьшей дисперсий. Если окажется, что различие между ними незначимо, то различие между остальными дисперсиями будет незначимо и подавно. В противном случае выбирается следующая пара дисперсий, имеющая максимальную разность и процедура сравнения их повторяется.

Пример 4.1. В первой декаде июля осуществлена съемка физических и химических характеристик воды Финского залива. При этом 8 гидрологических станций были выполнены в пределах акватории Невской губы до о. Котлин, а другие 9 станций – сразу же за о. Котлин. Средняя поверхностная температура воды до о. Котлин составилах=16,2 ^оС , а ее стандартное отклонение s_х = 3,2 ^oC. Средняя температура воды за о. Котлин оказалась заметно нижеy=13,9 ^oC при стандартном отклонении s_y= 2,1 ^oC. На уровне значимости α=0.05 выяснить насколько существенно влияние острова Котлин на распределение средней температуры воды и дисперсии в пределах проведения гидрологической съемки.

Прежде всего, рассмотрим равенство выборочных дисперсий. Нулевая гипотеза имеет вид Н₀ : s²_x = s²_y, а альтернативную гипотезу примем Н₁ : s²_x  s²_y. В этом случае критическая область является двусторонней. Рассчитываем фактическое значение критерия Фишера по формуле (4.3), которое равно F= 2,32. После этого определяем критическое значение статистики Фишера при числе степеней свободы ₁=n1=8, ₂=m1=7 и уровню значимости =0,05. Из приложения 4 находим, что F_кр(;₁,₂)=3,73. Так как F<F_кр, то мы можем полагать, что расхождения между выборочными дисперсиями не являются значимыми и, следовательно, влияние о. Котлин не сказывается на дисперсии температуры воды.

Рассмотрим теперь равенство выборочных средних. В соответствии с общей схемой проверки гипотез записываем нулевую гипотезу как Н₀ :х =y, т.е. средние значения температуры воды для обоих участков гидрологической съемки равны. В качестве альтернативной гипотезы возьмем гипотезу Н₁ :х >y, принятие которой означает существенное влияние о. Котлин на среднюю температуру воды. Наилучшим образом проверке гипотезы отвечает критерий Стьюдента. Поэтому рассчитываем его фактическое значение по формуле (4.1). Получаем t=1,62. Теперь определяем критическое значение статистики Стьюдента при числе степеней свободы =9+8–2=15 для односторонней области, соответствующей удвоенному уровню значимости, т.е. 2. Из приложения 3 находим t_кр(2=0,10,=15) =1.75. Поскольку t<t_кр, то у нас есть основания считать, что расхождения между выборочными средними не являются значимыми. Другими словами, влияние о. Котлин не сказывается существенно на среднем значении температуры воды.

Пример 4.2. Как известно, для подавляющего большинства районов Мирового океана характерно очень плохое покрытие его гидрометеорологическими данными вообще и температурой поверхности океана в частности. В связи с этим постоянно возникает вопрос о степени репрезентативности тех или иных архивов «реанализа», содержащих гидрологические характеристики и представляющих собой по существу некие «черные ящики». Естественно, для этого необходимы реперные данные. К их числу, безусловно, относятся уникальные гидрологические наблюдения, измеренные на судне погоды «М», расположенном почти в центре Норвежского моря.

Рассмотрим степень соответствия температуры поверхности океана в районе судна «М» (66^о с.ш. и 2^о в.д.) и полученной из глобального архива «реанализа» СDAS (Climate Data Assimilation System), сведения о котором приведены в разделе 1. Значения температуры из архива СDAS брались для двухградусного квадрата, центр которого (65,7 с.ш. и 1,9 в.д.) почти совпадает с местоположением судна «М».

В табл.4.2 приведены первичные статистические характеристики ТПО (выборочные средние и дисперсии) для отдельных месяцев за период 1951-2001 гг. (N=51), а также вычисленные критерии Стьюдента и Фишера.

Из сравнения средних видно систематическое занижение данных СDAS в течение всего года, которое колеблется в пределах 0,2-0,5 ^оС. В среднем за год оно равно 0,3 ^оС. Кроме того, в большинстве месяцев года проявляется занижение дисперсии данных СDAS, особенно значительное летом. Возникает вопрос – насколько существенны указанные расхождения в оценках средних и дисперсий. Отметим, что критическое значение критерия Стьюдента при =0,05 и =101 равно t_кр = 1,98, а критерия Фишера при =0,05 и  ₁ = 50, ₂=50 равно F_кр=1,60.

Таблица 4.2

Проверка соответствия средних значений и дисперсий ТПО в районе судна погоды «М» и точке с координатами 65,7 с.ш. и 1,9 в.д. для отдельных месяцев периода 1951-2001 гг.

Месяц	Среднее значение, оС		Дисперсия, оС		Критерий Стьюдента	Критерий Фишера
	«М»	СDAS	«М»	СDAS
Январь	6,65	6,38	0,19	0,12	3.40	1.58
Февраль	6,38	6,11	0,18	0,14	3.41	1.29
Март	6,38	5,99	0,14	0,16	3.06	1.17
Апрель	6,46	6,24	0,13	0,12	3.14	1.12
Май	7,39	7,18	0,15	0,11	2.91	1.40
Июнь	9,10	8,75	0,45	0,18	3.11	2.43
Июль	10,80	10,40	0,66	0,27	2.94	2.43
Август	11,70	11,20	0,69	0,25	3.65	2.76
Сентябрь	10,70	10,40	0,52	0,20	2.50	2.56
Октябрь	9,03	8,80	0,32	0,11	2.47	2.98
Ноябрь	7,78	7,58	0,25	0,09	2.42	2.78
Декабрь	7,10	6,83	0,20	0,10	3.46	1.98
Год	8,28	7,99	0,14	0,07	4.45	2.04

Как видно из табл.4.2. для всех 12 месяцев t > t_кр, т.е. различия между средними значениями значимы. Что касается сравнения величин дисперсий, то расхождения значимы в летне-осенний (июнь-декабрь) период, когда F > F_кр. В течение января-мая изменчивость ТПО по натурным данным и архива СDAS можно полагать близкой.

Достаточно очевидно, что главной причиной этих расхождений является наличие систематической ошибки в данных архива СDAS. Для ее устранения достаточно к значениям температуры за весь рассматриваемый период времени прибавить 0,3 ^оС. Действительно, пересчет после этого критерия Стьюдента показал, что для всех месяцев года уже выполняется условие t < t_кр. В то же время в соответствии со вторым свойством дисперсии ее величина остается постоянной для всех месяцев года, поэтому оценки критерия Фишера в табл. 4.2 не изменятся.

Итак, использование критериев Стьюдента и Фишера позволило выявить не только существенную нерепрезентативность среднемесячных значений ТПО в Норвежском море полученным из архива СDAS, но и в значительной степени устранить ее простым способом.