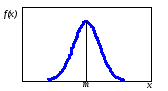
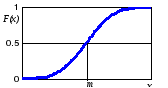
Нормальный закон распределения

Нормальный закон с плотностью (5.21) и функцией распределения

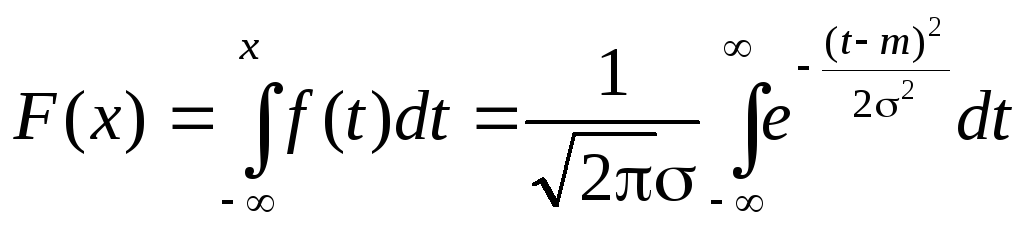
(5.25)

играет особую роль в теории вероятностей и математической статистике благодаря своим свойствам:

1. нормальная кривая является хорошим приближением биномиальной формулы при большом числе испытаний;

2. плотность нормального закона наименее информативна из всех распределений неограниченной СВ, поэтому ее лучше всего использовать для доопределения имеющихся сведений о СВ;

3. сумма большого числа СВ, среди которых нет превалирующих, подчиняется нормальному закону (центральная предельная теорема);

4. нормальный закон устойчив относительно сложения: сумма двух нормально распределенных СВ подчиняется нормальному закону.

Рассеивание снарядов является результатом влияния большого числа случайных факторов, среди которых нет превалирующих, поэтому его описывают нормальным законом. Ошибки целеуказания также распределены нормально. Сумма этих двух ошибок (промах) подчинена тому же закону.

Числовые характеристики

Рис. 5.8. Графики нормального распределения

В силу симметрии нормального распределения относительно значения x = m мода, медиана и МО совпадают: Mo = Me = m_x = m (рис. 5.8) Плотность модального значения обратно пропорциональна параметру . Это значит, что степень уплотнения наименьших отклонений СВ от среднего значения возрастает с умень­шением параметра , который, имея размерность случайной величины, играет роль СКО. Чтобы убедиться в этом, определим моментные характеристики:

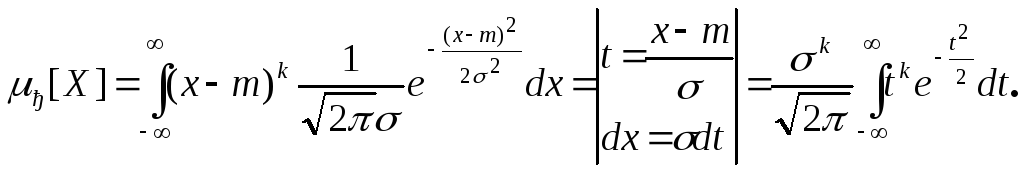
При нечетных k интеграл в симметричных пределах обращается в ноль. При четных k интегрированием по частям получим:

Первое слагаемое равно нулю, а второе выражается через исходный интеграл. Последний в рекуррентной цепочке интеграл I(0) = , так как представляет собой интеграл Пуассона при  = 0,5.

Получим для центральных моментов четных порядков общую формулу:

В частности,

Таким образом, параметры нормального распределения m,  – это , соответственно, МО и СКО распределения. Принадлежность СВ X к классу нормальных распределений будем обозначать XN(m, ).

Вероятность попадания в заданный интервал

Определение вероятности попадания СВ в заданный интервал – одна из основных практических задач. При известных параметрах нормального распределения m,  задача сводится к вычислению определенного интеграла

P(<X<) =.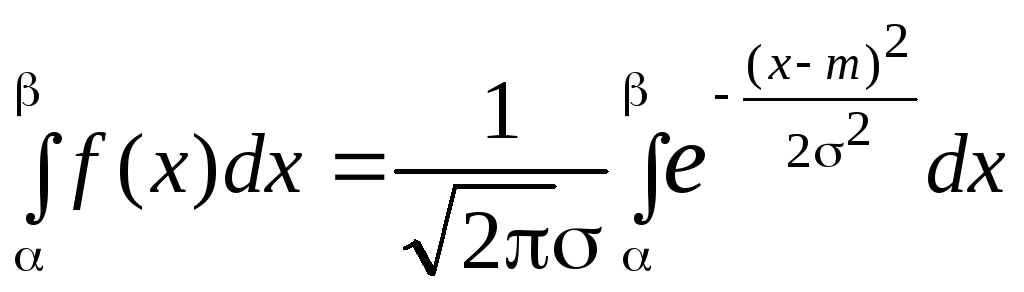

Если имеются значения функции распределения (5.11) на концах интервала, вычисление вероятности не составляет труда:

P(<X<) = F() – F().

Стандартное нормальное распределение

В справочниках имеются таблицы значений функции стандартного нормального распределения N₀(0,1) с параметрами m = 0,  =1. Эта функция имеет специальное обозначение ^*(x), но конечно обладает всеми свойствами функции распределения:

.

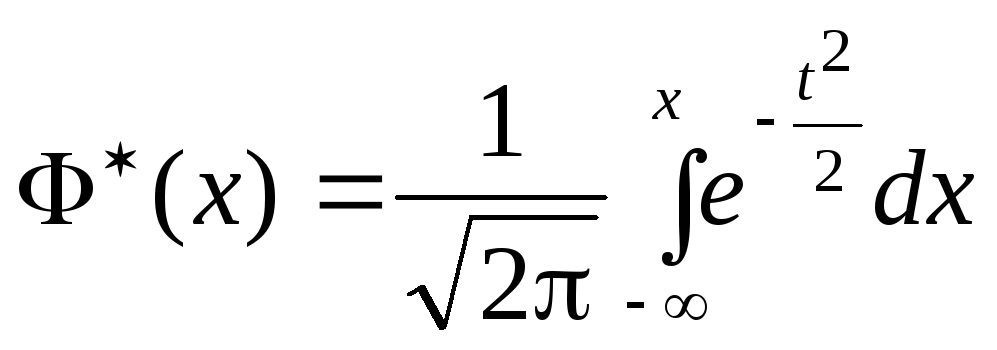(5.26)

Произвольную СВ X N₀(0,1) можно привести к стандартной переносом начала координат в центр рассеивания и изменением масштаба в  раз:

.

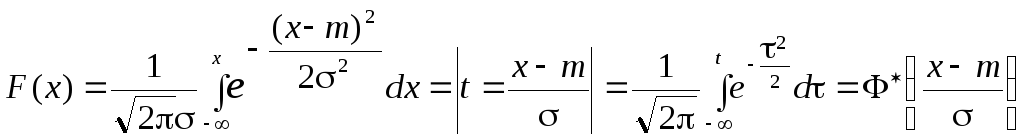С помощью таблицы стандартной функции нормального распределения вероятность попадания в заданный интервал можно вычислить по формуле

P(<X<) = Ф* – Ф*.

(5.27)