3.4. Криві другого порядку в полярній системі координат. Параметричні рівняння плоских кривих

На практиці| часто доводиться|припадати| мати| справу| з кривими| на площині|, які| не є| кривими другого порядку|ладу|, зокрема з|із| кривими третього|, четвертого і вищих порядків|ладів|. Найчастіше вони описують деякі траєкторії руху точок|, які задовольняють| певним умовам. У більшості випадків| рівняння| кривих вищих порядків можна записати в полярних координатах або| в параметричному вигляді|виді|, що| істотно|суттєвий| спрощує вид рівнянь і побудову| кривих.

Для побудови кривих в полярній системі координат задають певні значення і знаходять відповідні значення . Для зручності результати обчислень заносять в таблицю. Побудувавши відповідні точки, і сполучивши їх, отримують графік кривої.

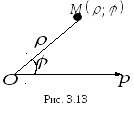
. Полярна система координат

Якщо на площині зафіксувати точку

(полюс) і промінь (полярну вісь),

то отримаємо полярну систему корди-

нат в якій положення довільної точки

площині визначається її відстанню

від точки , а також кутом

, який утворює промінь

з полярною віссю .

При цьому кут отримують поворотом полярній осі проти годинникової стрілки до збігу з променем .

Числа і називають полярними координатами точки (рис. 3.13).

. Розглянемо деякі лінії, рівняння яких задані в полярній системі координат.

коло з центром в полюсі і радіусом, рівним .

2. Криву, що описується точкою

кола з радіусом , яке котиться

без ковзання ззовні по колу рівного

радіуса, називають кардіоїдою.

Рівняння кардіоїди в полярній

системі координат має вид (рис. 3.35)

. (3.48)

Відмітимо, що назва кривої

пов’язана з тим, що її форма нагадує

серце.

3. Спіраль Архімеда – це траєк-

торія точки, що рівномірно рухається

(з швидкістю ) вздовж прямої, яка

рівномірно обертається (з кутовою

швидкістю ) навколо заданої точки

– полюса.

Її рівняння в полярних коорди-

натах (рис. 3.36)

, (3.32)

де параметр спіралі.

.

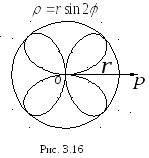4. Чотирьохпелюсткова роза

утворюється множиною основ перпенди-

кулярів, опущених з вершини пря-

мого кута на відрізок сталої довжини,

кінці якого ковзають по сторонах цього

прямого кута (рис. 3.16).

Рівняння цієї кривої в полярних

координатах

, (3.33)

де радіус кола, в яке «вписано»

розу.

Зауважимо, що рівняння

визначає пелюсткову розу, причому

роза має пелюсток, якщо непарне число, і пелюсток, якщо парне. Крім того роза повністю розміщується всередині кола радіуса .

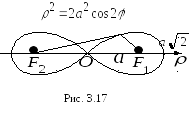5. Лемніската Бернуллі утворюється множиною всіх точок площини, для кожної з яких добуток

відстаней до двох заданих точок

і , є величиною сталою і

дорівнює квадрату половини від-

стані між цими точками (рис. 3.17).

Рівняння лемніскати в

полярних координатах має вигляд

. (3.34)

. Наведемо приклади деяких ліній, рівняння яких задані параметрично.

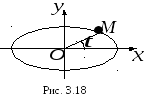1. Параметричні рівняння еліпса

, , . (3.53)

В параметричних рівняннях еліпса

параметр є кутом, який утворює

відрізок з віссю абсцис (рис. 3.18).

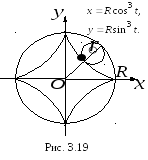
Астроїда – це траєкторія

фіксованої точки кола радіуса ,

яка котиться без ковзання по

внутрішній стороні кола радіуса

(рис. 3.19).

Параметричні рівняння

астроїди мають вигляд:

; ,

. (3.36)

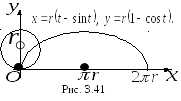3. Циклоїда – це траєкторія,

фіксованої точки кола радіуса ,

яка котиться без ковзання уздовж

прямої – осі (рис. 3.20).

Параметричні рівняння

циклоїди мають вигляд:

; , (3.37)

Зведемо рівняння розглянутих кривих в таблицю