2.2. Преобразование Лапласа

Для анализа и синтеза САУ в ТАУ широкое распространение при решении дифференциальных уравнений получил операторный метод. Его основным достоинством является сведение решения системы дифференциальных уравнений к решению системы нормальных алгебраических уравнений.

В основе операторного метода лежит преобразование Лапласа:

, (2.3)

которое устанавливает соответствие между функцией действительной переменной t {x(t)} и функцией комплексной переменной p {Х(р)}, где ; j – мнимая единица, т.е. ;  - круговая частота. Функция времени x(t), входящая в интеграл Лапласа (2.3) называется оригиналом, а результат интегрирования – функция X(p) – изображением функции x(t) по Лапласу.

Предполагается, что функция x(t), которая подвергается преобразованию Лапласа обладает следующими свойствами:

- x(t) определена и кусочно-дифференцируема на всей положительной числовой полуоси [0, +);

- x(t) =0 при t<0;

- существуют такие положительные числа M и с, что

при .

Соотношение

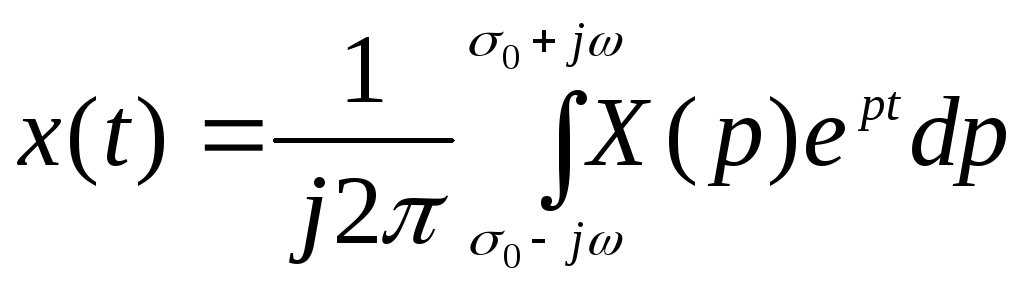, (2.4)

определяющее по известному изображению его оригинал (в точках непрерывности последнего) называется обратным преобразованием Лапласа, которое символически можно записать так:

. (2.5)

2.2.1. Основные свойства преобразования Лапласа

1. Свойства линейности:

а) x(t)=ax₁(t) X(p)=aX₁(p).

б) x₁(t) x₂(t) X₁(p) X₂(p).

2. Дифференцирование оригинала.

При нулевых начальных условиях дифференцированию оригинала соответствует умножение изображения на параметр p:

3. Интегрирование интеграла.

Интегрирование оригинала сводится к делению изображения на параметр р:

.

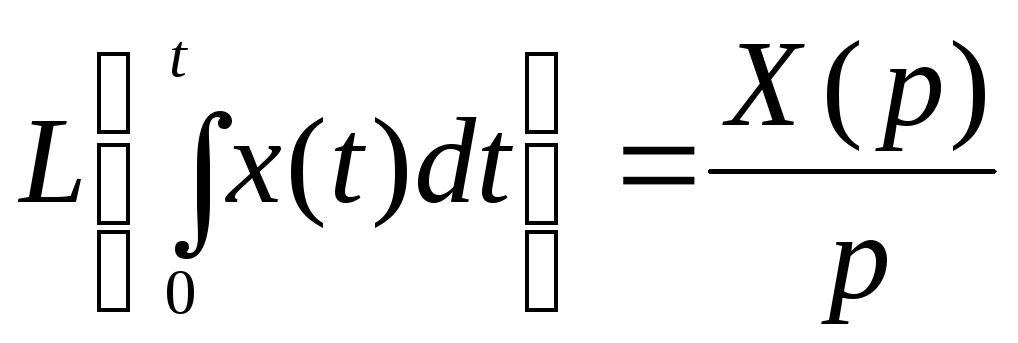4. Теорема запаздывания (смещение аргумента оригинала).

Для любого положительного числа 

5. Теорема подобия (изменение масштаба времени).

.

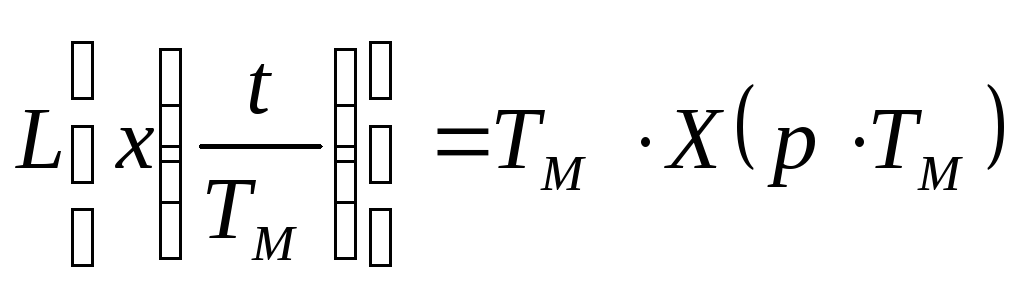6. Теорема о свертке (теорема умножения изображений).

Если x₁(t), x₂(t) – оригиналы, а X₁(p), X₂(p) – их изображения по Лапласу, то

.

7. Теорема о начальном значении оригинала.

.

8. Теорема о конечном значении оригинала.

.

2.3. Передаточные функции

Запишем дифференциальное уравнение одномерного объекта

(2.6)

Умножив все составляющие выражения (2.6) на и взяв интеграл по каждому слагаемому от 0 до + и учитывая свойства преобразования Лапласа получим дифференциальное уравнение в операторной форме вида:

(2.7)

Вынеся за скобки изображения Y(p) и U(p) получим уравнение вида:

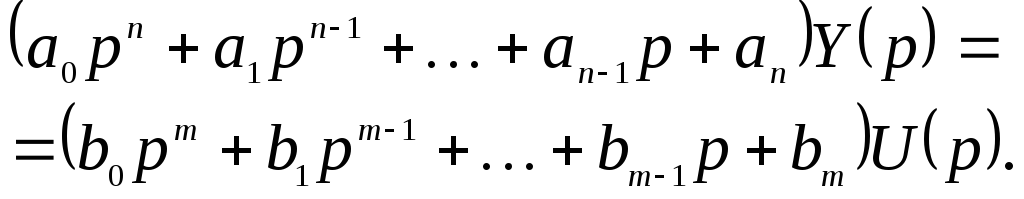(2.8)

Введем следующие обозначения:

;

.

Тогда уравнение (2.8) можно записать в виде:

. (2.9)

Откуда

. (2.10)

Введем обозначение:

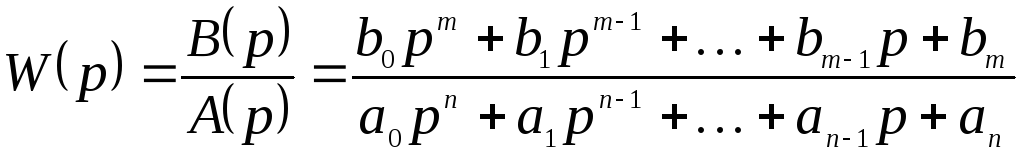. 2.11)

Тогда имеем, что

. (2.12)

Функция W(p) называется передаточной функцией и представляет собой отношение изображения по Лапласу выходной переменной к изображению по Лапласу входной переменной при нулевых начальных условиях, т.е.

. (2.13)

Формально передаточная функция получается из дифференциального уравнения путем замены в нем символов кратного дифференцирования на соответствующую степень и делением образованного таким образом многочлена правой части на многочлен левой части. Знаменатель передаточной функции (2.11) называется характеристическим полиномом, а приравненный нулю характеристическим уравнением. Коэффициенты полиномов являются вещественными величинами, определяемыми физическими параметрами системы.

Свойства передаточной функции САР.

1. Передаточная функция является правильной рациональной дробью, для которой выполняется условие: .

2. Все коэффициенты и являются вещественными величинами.

3. Нули (корни полинома в числителе) и полюса (корни полинома в знаменателе) могут быть вещественными или комплексно-сопряженными.