4. Устойчивость линейных систем автоматического управления

4.1. Понятие устойчивости системы

Понятие устойчивости САУ связано с способностью системы возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. Система считается устойчивой, если будучи выведенной из состояния равновесия, возвращается к этому состоянию, после снятия причин, вызвавших отклонение. Система неустойчива, если она не возвращается в состояние равновесия, из которого ее вывели, а отдаляется от него.

Введем понятия: устойчивость в малом и устойчивость в большом. Система устойчива в малом, если она устойчива при бесконечно малых возмущениях. Система устойчива в большом, если она устойчива при всех возмущениях, возможных в системе.

Запишем выходную переменную в виде:

, (4.1)

где y_пер(t) – переходная составляющая; y_уст(t) – установившаяся составляющая. Система будет устойчива, если с течением времени при t переходная составляющая будет стремиться к нулю, т.е. y_пер(t)=0. Причем устойчивость системы всегда закладывается в систему на этапе проектирования.

Дифференциальное уравнение САР при нулевых начальных условиях имеет вид:

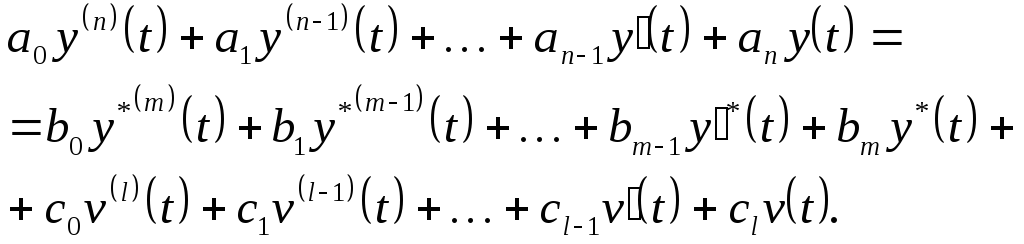(4.2)

Для оценки устойчивости САР исследуется свободная составляющая решения уравнения (4.2), т.е. решение однородного дифференциального уравнения вида:

, (4.3)

которое оценивает свободное движение системы. Данное уравнение, записанное в операторной форме

(4.4)

представляет собой характеристическое уравнение системы, корни которого p₁, p₂, …,p_n определяют характер переходного процесса. Решение однородного дифференциального уравнения имеет вид:

, (4.5)

где с₁, с₂,…, с_п - постоянные интегрирования, определяемые из начальных условий. При этом корни характеристического уравнения определяются только видом левой части уравнения (4.2), а постоянные интегрирования определяются также и правой частью уравнения (4.2). Другими словами, быстрота затухания и форма переходного процесса определяются и левой и правой частью исходного дифференциального уравнения (4.2).

Поскольку в понятие устойчивости системы входит только факт наличия или отсутствия переходного процесса, то устойчивость определяется только характеристическим уравнением системы.

Корни характеристического уравнения могут быть: вещественными; мнимыми и комплексно-сопряженными. Эти корни изображаются в виде точек на комплексной плоскости корней, что отражено на рис. 4.1.

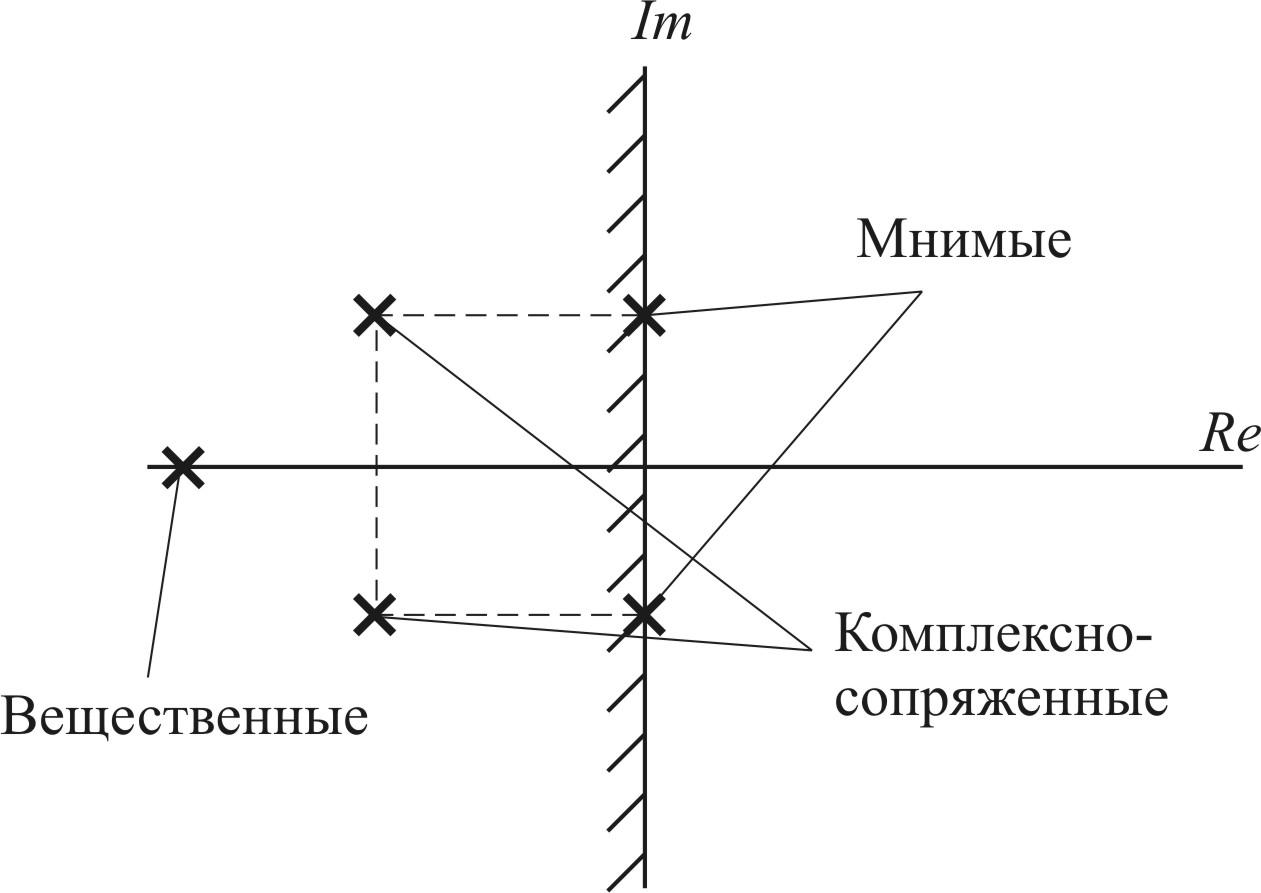
Рис. 4.1. Комплексная плоскость корней

Необходимым и достаточным условием устойчивости системы по Ляпунову является условие, при котором все вещественные корни характеристического уравнения являются отрицательными, а комплексно-сопряженные корни имеют отрицательную вещественную часть. Система находится на границе устойчивости, если имеется нулевой или бесконечный корни, или пара чисто мнимых корней.

Таким образом, для устойчивости системы необходимо и достаточно, чтобы все корни характеристического уравнения лежали слева от мнимой оси плоскости корней, которая является границей устойчивости в плоскости корней.

Нахождение корней характеристического уравнения является весьма трудной задачей, т.к. отыскание корней алгебраических уравнений высокой степени возможно только с применением громоздких численных методов. Поэтому на практике для исследования устойчивости систем широко используются критерии устойчивости.

Критерии устойчивости представляют собой правила исследования устойчивости систем без непосредственного решения дифференциальных уравнений.

Критерии устойчивости подразделяются на два больших класса:

- алгебраические критерии устойчивости, которые устанавливают необходимые и достаточные условия отрицательности корней в форме ограничений, накладываемых на определенные комбинации коэффициентов характеристического уравнения;

- частотные критерии устойчивости, определяющие связь между устойчивостью системы и формой частотных характеристик.

При анализе устойчивости систем обычно решают одну или несколько следующих задач:

- оценивают устойчива или неустойчива система при заданных параметрах системы;

- определяют допустимый по условию устойчивости диапазон изменения некоторых незаданных параметров системы;

- выясняют, может ли система при заданной структуре в принципе быть устойчивой.