Метод хорд

Предполагаем, что мы нашли отрезок [a,b] на концах которого функция F(x) меняет знак

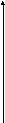y

B

0 a c b x

A

В методе хорд, как и в методе половинного деления на каждом итерационном шаге происходит последовательное сужение отрезка [a,b] содержащего корень. В методе хорд на каждом итерационном шаге в качестве одного из концов такого суженного отрезка берется точка пересечения хорды АВ с осью х.

Получим соотношение для определения точки С.

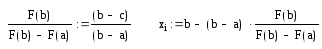
[a,x_i], [x_i,b]

Итерационный процесс повторяем до тех пор, пока не будет достигнута заданная точность. Так же как и метод половинного деления, гарантированно сходится, однако в ряде случаев он имеет более быструю сходимость.

Метод №13

Метод Ньютона (касательных)

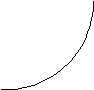
Метод Ньютона сходим с методом хорд. Его отличие от метода хорд состоит в том, что на каждом итерационном шаге вместо хорды проводится касательная к кривой y=f(x) и ищется точка пересечения касательной с осью абсцисс, которая и определяет следующее приближение корня.

y y=f(x)

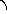α

0 x_i+1 x_i x

Получим формулу для определения корня на i+1 итерационном шаге.

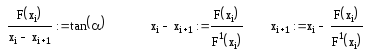
На каждом итерационном шаге объем вычислений в методе Ньютона несколько больше, чем в ранее рассмотренных методах, потому что приходится находить значение функции F(x), по ее производной. Однако скорость сходимости метода Ньютона в ряде случаев значительно выше, чем в других методах. Поэтому метод Ньютона является одним из самых распространенных методов решения нелинейных уравнений. Сходимость метода Ньютона в значительной степени зависит от выбора начального приближения х₀. Чем ближе х₀ к корню, тем сходимость лучше, поэтому иногда целесообразно использовать смешанный алгоритм. Во всех итерационных процессах ошибка округления не накапливается – это является одним из важнейших преимуществ итерационных методов.

Определенными особенностями обладают нахождение корней алгебраических уравнений.

Корни алгебраического уравнения в ряде случаев можно находить последовательно. Предположим сначала методом половинного деления нашли корень уравнения x_i, после этого получаем:

Тема 4: Решение систем линейных уравнений

Системы линейных уравнений научно-исследовательской инженерной практики встречаются весьма часто. К решению систем линейных уравнений сводятся многочисленные практические задачи. С использованием численных методов Ех Коэффициенты сплайнов находятся путем решения Систем линейных уравнений. К системам линейных уравнений приводят уравнения частных производных.

Задачи на нахождение собственных значений так же приводят к СЛАУ. Таким образом, решение СЛАУ – одна из самых распространенных и важных задач высшей математики.

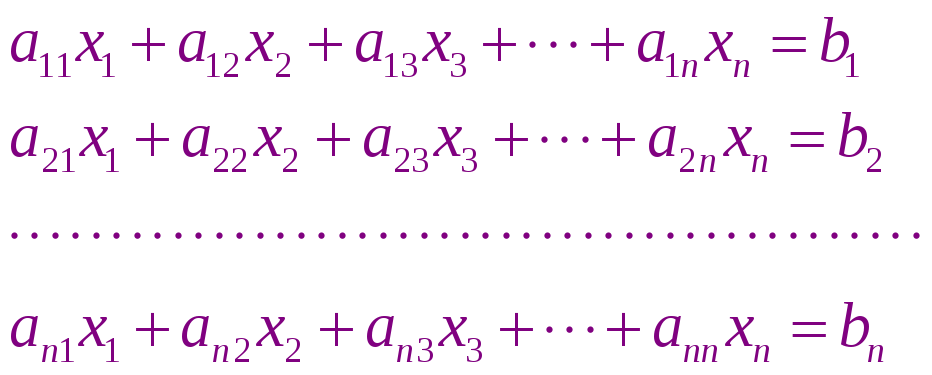
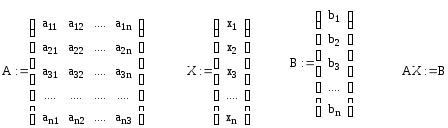
Важнейшей характеристикой квадратной матрицы является ее определитель(D)

В курсе высшей математики показывается, что система линейных алгебраических уравнений имеет единственное решение, если определитель системы не равно 0, в этом случае решение может быть найдено с помощью Крамера, где D_i определитель матрицы, которое получается после исключения в матрице А i-го столбца и его замены столбцом свободных членов.

Если определитель системы D=0, то в этом случае матрица D называется вырожденной, а системы либо не имеют решения, либо имеет бесчисленное множество решений. Для некоторых систем оказывается очень чувствительны к малым погрешностям исходных данных. Такие системы называются условно обустроенные. Определение плохо обусловленных систем близок к нулю. Всегда надо иметь в виду это. Некоторые неконкретные задачи приводят к плохо обусловленным системам уравнений. Эти задачи могут иметь важное практическое значение. Существуют методы решения таких задач. Методы решения систем уравнений делятся на 2 большие группы: прямые и итерационные. Прямые методы используют методы, которые наиболее универсальны, но они образуются недостатками: они требуют хранения в оперативной памяти сразу всей матрицы, поэтому прямые методы используют обычно, если n не превосходит несколько 100. В итерационных методах решение находится путем последовательности, в этих методах накопленная погрешность не превосходит, поэтому их можно использовать для решения больших систем уравнений. Однако сходимость итерации может быть очень медленно. Время счета может оказаться слишком большим. В них решаются ограниченный класс уравнений. Метод Крамера относится к прямому методу, однако, на практике метод Крамера практически некогда не используется, так как он требует большого объема вычислений. Оценим объем вычислений методом Крамера: N=(n+1)n n! n с ростом n малое резко возрастает n=6 N>10000000.

Метод №14