
- •Тема1: Модели и моделирование
- •Пример построения математической модели:
- •Погрешности численных методов
- •Свойства численного решения
- •Тема2 Аппроксимация функций
- •Интерполяционная формула Лагранжа
- •Сплайны
- •Сплайны третьей степени
- •Метод наименьших квадратов
- •Тема 3: Решение нелинейных уравнений
- •Метод половинного деления
- •Метод простых итераций
- •Метод хорд
- •Метод Ньютона (касательных)
- •Тема 4: Решение систем линейных уравнений
- •Метод Гаусса
- •Метод прогонки
- •Метод уточнения решения
- •Метод Гаусса-Зейделя
- •Тема5: Решение систем нелинейных уравнений
- •Простой итеррации
- •Метод Ньютона
- •Метод возмущения параметров
- •Тема 6: Численное интегрирование
- •Метод определенного интеграла
- •Метод трапеции
- •Метод Симпсона
- •Метод Гаусса
- •Метод Монте-Карло
- •Метод Монте-Карло для вычисления кратных интегралов
- •Решение обыкновенных дифференциальных уравнений (оду)
- •Метод Эйлера
- •Модифицированный метод Эйлера
- •Метод Рунге – Кутта
- •Метод Рунге-Кутта для решения систем оду
- •Метод Рунге-Кутта для оду высших порядков
- •Метод стрельбы
- •Метод конечных разностей (мкр) (метод сеток).
- •Решение дифференциальных уравнений с частными производными
- •Явная разностная схема для уравнения теплопроводности
- •Неявная разностная схема для уравнения теплопроводности
- •Задачи оптимизации.
- •Метод половинного деления
- •Метод золотого сечения
- •Метод покоординатного подъёма (спуска)
- •Метод градиентного подъёма (спуска)
- •Метод наискорейшего подъёма
- •Задания для самостоятельной проработки
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСУДАРСТВЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ЮЖНО-РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕСИТЕТ
(НОВОЧЕРКАССКИЙ ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ)»

ВЫПОЛНИЛ:
СТУДЕНТ ФМФ II-1
КАПЛУНОВ НИКОЛАЙ
ПРЕПОДАВАТЕЛЬ:
КНЯЗЕВ СЕРГЕЙ ЮРЬЕВИЧ
НОВОЧЕРКАССК 2008
Содержание
Тема №1.
Модели и моделирование.
Погрешности численных методов.
Свойства численного решения.
Тема №2
Аппроксимация функций.
Метод 1. Интерполяционная формула Лагранжа.
Метод 2. Сплайны.
Метод 3. Сплайны третьей степени.
Метод 4. Метод наименьших квадратов.
Тема № 3
Решение нелинейных уравнений.
Метод 10. Метод половинного деления.
Метод 11. Метод простых итераций.
Метод 12. Метод хорд.
Метод 13. Метод Ньютона (касательных).
Тема № 4.
Решение систем линейных уравнений.
Метод 14. Метод Гаусса.
Метод 15. Метод прогонки.
Метод 16. Метод уточнения решения.
Метод 17. Метод Гаусса-Зейделя.
Тема № 5.
Решение систем не линейных уравнений.
Метод 18. Метод простой итерации.
Метод 19. Метод Ньютона для системы уравнений.
Метод 20. Метод возмущения параметров.
Тема № 6.
Численное интегрирование.
Метод 21. Метод прямоугольников
Метод 22. Метод трапеций.
Метод 23. Метод Симпсона
Метод 24. Метод Гаусса.
Метод 26. Метод Монте-Карло.
Метод 27. Метод Монте-Карло для вычисления кратных интегралов.
Тема № 7.
Решение обыкновенных дифференциальных уравнений (ОДУ).
Метод 28. Метод Эйлера.
Метод 29. Модифицированный метод Эйлера.
Метод 30. Метод Рунге-Кутта.
Метод 31. Метод Рунге-Кутта для решения систем ОДУ.
Метод 32. Метод Рунге-Кутта для ОДУ высших порядков.
Метод 33. Метод стрельбы.
Метод 34. Метод конечных разностей (МКР) (метод сеток).
Тема № 8.
Решение дифференциальных уравнений с частными производными.
Уравнение теплопроводности.
Метод 35. Явная разностная схема для уравнения теплопроводности.
Метод 36. Не явная разностная схема для уравнения теплопроводности.
Тема №9.
Задачи оптимизации.
Метод 37. Метод половинного деления.
Метод 38. Метод золотого сечения.
Метод 39. Метод покоординатного подъёма (спуска).
Метод 40. Метод градиентного подъёма (спуска).
Метод 41. Метод наискорейшего подъёма.
Тема № 10.
Задания для самостоятельной проработки.
Транспортная задача.
Задача о ресурсах.
Волновое уравнение.
Уравнение Лапласа.
Тема1: Модели и моделирование
Используется 3 моделирования:
В научной и инженерной практики возникают задачи исследования разложения предметов, свойств и т.д. Эти задачи можно решать экспериментально, но он не всегда разумен: вследствие высокой стоимости, уникальности, недоступности.
Например: недра звезд и планет не доступны, при конструировании самолета требуются особые исследования. Во всех этих случаях реальные явления – объект (оригинал) заменяется его моделью. Исследование явлений объектов с помощью моделей называется моделированием. Существует множества видов модели: если модель и моделированный объект имеют оду и ту же физическую природу, то говорят о физической модели, при конструировании физической модели необходимо выделить существующие черты и свойства оригинала, наоборот второстепенные черты и свойства объекта можно не учитывать. Простейшей физической моделью является математическая точка (частица). Единственным существенным свойством частицы является масса. Всеми основными свойствами частицы (форма, состав, цвет, температура, вкус, запах и т.д.) можно пренебречь. При использовании модели необходимо четко представлять в каких условиях и для исследования, каких явлений применение данной модели конкретно.
Например: физическая модель частицы может применяться для исследования механического движения тел, размеры которых малы в сравнении с характерным масштабом задачи.
В качестве физической модели могут использоваться некоторые математические конструкции, необходимым условием физической модели в этом случае является геометрическое и физическое подобие модели и оригинала. Это означает, что сходственные моменты времени и в подобных точках пространства значение величин характеризующих явление для модели и оригинала должны быть пропорциональны друг другу, это позволяет производить пересчет результатов получения с помощью модели для оригинала. Для этого необходимо из величин характеризующих явление конструирования безразмерные комбинации, которые называются критериями подобия. Физически подобны будут модель и оригинал в том случае если критерии подобия для них имеют одинаковые значения.
Например: исследование течения жидкости по трубам различного диаметра, очевидно, что характер течения зависит от скорости, диаметра, плотности все они являются размерными, но из них можно сконструировать безразмерную величину число Рейнольдца:
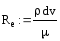
Физически подобными будут течения с одинаковым числом Рейнольдца. Некоторые явления можно исследовать путем изучения какого-либо явления иной физической природы, но описываемого теме же математическими соотношениями, что и моделируемое явление.
Например: электрические и механические колебания и наоборот, такое моделирование называется аналоговое. Физическую модель можно исследовать экспериментально, однако есть другой весьма эффективный способ исследования модели и решения с ее помощью задач, для этого на основе физических законов и других соображений.
Например: предположение, имеющее характер гипотез строится система математических соотношений (равенства, неравенства уравнений, других логических конструкций), эти соотношения отображают с помощью математических символик содержащую постановку математических задач. Совокупность этих соотношений называется математической моделью, а решение задачи с помощью математической модели называется математическим моделированием. Процесс математического моделирования подразделяют на 3 этапа:
Первым этапом математического моделирования является подстановка задачи, определение объекта и цели исследования, определение факторов изучения, формулирование законов связывающих объекты и факторы модели. Первый этап завершается записью математических терминов соотношения между объектами модели, тем самым физическая или техническая задача сводится к математической задачи. Первый этап моделирования – построение математической модели является одним из наиболее сложных и ответственных этапов работы. Трудность первого этапа связан с необходимостью соединения математических и специальных знаний и с возможной неопределенностью и неоднозначностью задачи.
Значение этапа:
Правильно выбранная математическая модель решает поставленную задачу наполовину. Математическая модель не определяется однозначно исследовательным объектом. Для ее разработки необходимо сформулировать упрощающие предположения лежащие в основе модели. Установить такие факторы необходимо (установить степень точности).
На втором этапе производится исследование математической задачи, ее решение иногда возможно аналитическое решение полученной математической задачи, однако в большинстве случаев это не удается, в этом случае для решения задачи используют численные методы.
На третьем этапе выясняется вопрос о достоверности полученных результатов о согласии теоретических следствий модели с реально наблюдаемыми результатами. При этом делается вывод о правильности и неправильности положений, лежащих в основе математической модели и в случае необходимости рассматриваемая модель уточняется или утверждается. Основным критерием является эксперимент, практика. Исследование задач обычно начинается с построения и анализа простейшей и наиболее грубой модели, а в дальнейшем решается вопрос о дальнейшем уточнении модели.
