Метод конечных разностей (мкр) (метод сеток).

Одним из универсальных методов решения краевых задач является метод конечных разностей.

Рассмотрим применение МКР для решения линейного дифференциального уравнения второго порядка.

Пусть требуется найти дифференциальное уравнение:

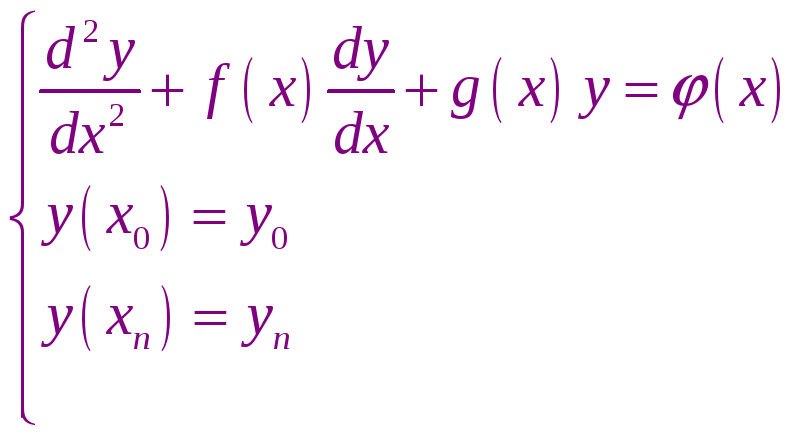
заданы краевые условия

Разбиваем отрезок узловыми равноотстоящими точками на частных отрезков. В каждой внутренней узловой точке аппроксимируем, производные с помощью разностных соотношений и записываем решаемое дифференциальное уравнение (1) для каждой внутренней узловой точки. В результате получается система алгебраических уравнений для нахождения неизвестных значений функции

Рассмотрим узловую точку

Аппроксимируем решаемое дифференциальное уравнение для узловой точки . Для этого

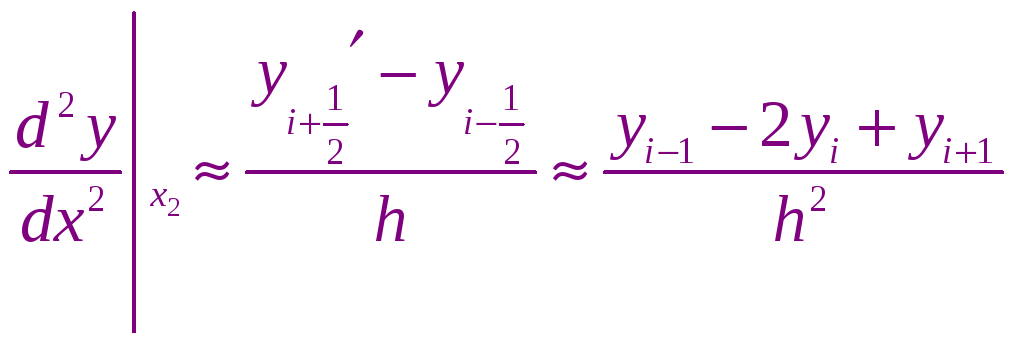получили приблизительное значение производной.

Подставим найденные значения в дифференциальное уравнение. Найдем, что в узле дифференциальное уравнение приблизительно заменяется следующим алгебраическим уравнением:

Аналогичное соотношение можно записать для каждого внутреннего узла. В результате получается система линейных алгебраических уравнений; число этих уравнений равно числу неизвестных значений , решаем систему и находим неизвестные.

Замечание: полученная система СЛАУ имеет трехдиагональную матрицу, поэтому решать полученную систему удобно с помощью метода прогонки.

Тема №8 Решение дифференциальных уравнений с частными производными.

Во многих практических важных задачах искомая функция зависит от нескольких переменных. Например, от трех координат и времени. Дифференциальные уравнения, описывающие такие задачи, могут содержать частные производные от искомой функции, такие уравнения называют дифференциальными уравнениями с частными производными. Наиболее практическое значение имеют дифференциальные уравнения с частными производными первого и особенно второго порядка. Такие уравнения называют уравнениями математической физики.

Различают уравнения математической физики трех типов:

1. параболический

2. гиперболический

3. эллиптический.

Тип уравнения зависит от соотношений между коэффициентами перед старшими производными. Способ решения уравнения математической физики существенным образом зависит от типа уравнения.

Существует множество аналитических методов решения уравнения математической физики. Однако круг задач, решаемых аналитически, весьма ограничен и поэтому для решения уравнения математической физики применяют численные методы. Таких методов тоже очень много. Мы рассмотрим один из них.

Этот метод относится к универсальным методам решения. Этот метод наиболее изучен и разработан. Широко используется также метод конечных элементов (МКЭ), метод граничных элементов (МГЭ) и другие методы.

Рассмотрим решение уравнения параболического типа с помощью метода сеток. Типичным примером одномерного уравнения параболического типа является уравнение теплопроводности:

Уравнение теплопроводности.

- температура в точке с координатой в момент времени

- коэффициент теплопроводности.

Любое уравнение параболического типа с постоянными коэффициентами путем соответствующих преобразований (поворотом системы координат в пространстве и изменением начала координат) может быть приведено к следующему виду:

- каноническая форма уравнения параболического типа.

Уравнение теплопроводности - параболическое уравнение. Для его решения необходимо дополнить начальными и граничными условиями.

- задает распределение температуры в начальный момент времени.

- температура на левой границе

- температура на правой границе

Граничные условия могут иметь и другой вид они могут накладывать ограничение на производную.

Численное решение поставленной задачи основано на введение разностной сетки в области решения задачи. Значение производных, начальные и граничные условия выражаются через значения функций в узлах сетки, в результате чего получается система алгебраических уравнений, называемая разностной схемой. Решая эту систему можно найти значение искомой функции в узлах сетки. Построение разностной схемы начинается с введения сетки в рассмотренную область пространства. Наиболее простыми и самыми распространенными являются прямоугольные сетки. Например, для решения задачи можно построить прямоугольную разностную сетку с шагом по координате и шагом по времени .

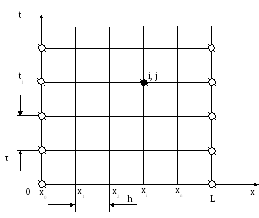
Можно использовать сетки с неравномерным шагом и даже не прямоугольные сетки. Все зависит от конкретных условий задачи.

Коэффициенты узлов сетки имеют значения:

Этот узел будем обозначать .

Значение искомой функции в узле обозначим . Совокупность этих значений образует сеточную функцию, которая аппроксимирует значение температуры в узлах сетки.

При построении конечно-разностной схемы используется некоторый шаблон, показывающий расположение смежных узлов в двух или более слоях, которые используют при аппроксимации производных конечно-разностными соотношениями. При построении конечно-разностной схемы может использоваться следующий шаблон.

Метод 35