При U = 104 В энергия электрона равна 104 эВ=1,65·10-15 Дж. Оценим импульс электрона: p = 2meU = 5 10−23 кг мс .
Следовательно, px = 5·10-23·10-4 = 5·10-27 кг·м/с, тогда:
x = |
2 |
≈10−8 м =10−5 мм =10−3 r |
|
||
|
px |
|
Т.е. движение электрона в электронно-лучевой трубке практически неотличимо от движения по траектории.
§48. Уравнение Шредингера
В 1926 г. развивая идеи де Бройля о волновых свойствах вещества, Шредингер получил свое уравнение. Оно позволяет найти волновые функции частиц, движущихся в различных силовых полях.
− |
2 |
ΔΨ +UΨ = i |
∂Ψ |
, |
(48.1) |
|
|
||||||
2m |
∂t |
|||||
|
|
|
|
|||
где m - масса частицы, i - мнимая единица, U - потенциальная энергия, |
- оператор Лапласа, |
|||||
результат действия которого на некоторую функцию представляет собой сумму вторых частных производных по координатам:
|
∂2Ψ ∂2Ψ ∂2Ψ |
|
ΔΨ = |
∂x2 + ∂y2 + ∂z2 . |
(48.2) |
Из (48.1) следует, что вид волновой функции определяется функцией U, т.е. характером сил, действующих на частицу.
Уравнение Шредингера является основным уравнением релятивистской механики. Оно не может быть выведено из других соотношений. Шредингер установил свое соотношение, исходя из оптико-механической аналогии.
Для одномерного случая придем к уравнению Шредингера. В этом случае оператор Лапласа определяется выражением:
ΔΨ = |
∂2 |
Ψ |
. |
(48.3) |
|
∂t 2 |
|||||
|
|
|
|||
Пусть частица движется свободно. Согласно идее де Бройля ей нужно сопоставить плоскую волну:
Ψ = Aexp[(i )(px − Et)]. |
(48.4) |
Продифференцируем эту функцию дважды по x и один раз по t. Получим:
∂Ψ |
= − i |
EAexp[(i )(px − Et)]= − i |
EΨ |
|
∂t |
|
|
|
|
или |
|
|
|
|
|
|
∂Ψ = − i |
E Ψ , |
(48.5) |
|
|
∂t |
|
|
|
|
∂2Ψ = − p2 |
2 Ψ . |
(48.6) |
|
|
∂x2 |
|
|
Отсюда:
24
p2 = − |
1 |
2 ∂2Ψ |
|
|||
Ψ |
∂x2 . |
(48.7) |
||||
|
1 |
|
||||
E = |
i |
∂Ψ |
|
|||
|
∂t |
|
||||
|
Ψ |
|
|
|||
В нерелятивистской механике энергия Е и импульс р свободной частицы связаны соотношением:
|
|
|
|
|
|
|
|
|
Ek = |
p2 |
. |
|
|
|
|
|
(48.8) |
|||||
|
|
|
|
|
|
|
|
|
2m |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда подставим (48.6) и (48.7) в (48.5) и получим: |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
− |
|
|
|
2 |
∂2Ψ |
= i |
∂Ψ |
. |
|
|
(48.9) |
|||||||
|
|
|
|
2m |
∂x2 |
|
∂t |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Это уравнение (48.9) совпадает c уравнением (48.1), если U=0. |
|
|||||||||||||||||||||
Если частица движется в силовом поле, характеризуемом потенциальной энергией U, то |
||||||||||||||||||||||
энергия и импульс связаны соотношением: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
p2 |
|
= E −U. |
|
|
|
|
|
(48.10) |
||||||
|
|
|
|
|
|
|
|
2m |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Используя выражение (48.7), получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
− |
1 |
|
|
|
|
|
|
∂ |
2Ψ |
= |
|
1 |
|
i |
∂Ψ |
−U . |
(48.11) |
|||||
Ψ 2m |
∂ x2 |
|
Ψ |
|
∂t |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
Умножив это соотношение на Ψ и перенеся член UΨ влево, придем к уравнению: |
|
|||||||||||||||||||||
|
− |
2 |
|
∂2 |
Ψ |
+UΨ = i |
∂Ψ |
. |
(48.12) |
|||||||||||||
|
2m |
∂x2 |
|
∂t |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Уравнение (48.12) совпадает с уравнением (48.1).
Для стационарного силового поля (постоянного во времени) Ψ не зависит от t:
Ψ(x, y, z,t) =ϕ(x, y, z) e−i Et ,
где E – полная энергия частицы.
Тогда дифференциальное уравнение принимает вид:
|
2 |
|
E |
|
|
E |
|
|
|
E |
|
E |
|
|
− |
|
exp −i |
|
t |
ϕ +Uϕexp −i |
|
t |
= i |
−i |
|
ϕ exp −i |
|
t . |
|
2m |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(48.13)
(48.14)
Сократив на общий множитель exp[- i (E/ħ) t], придем к дифференциальному уравнению, определяющему функцию φ:
2 |
|
ϕ +Uϕ = Eϕ . |
(48.15) |
||
− |
|
|
|||
2m |
|||||
Уравнение (48.15) называется – уравнение Шредингера для стационарных состояний. |
|
||||
Это уравнение часто записывают в виде (48.16): |
|
||||
ϕ + |
2m |
(E −U )= 0 . |
(48.16) |
||
2 |
|||||
В случае стационарного силового поля волновая функция имеет вид (48.13), соответственно:
|
|
|
E |
|
|
|
E |
|
|
ϕϕ |
|
= exp i |
|
t ϕ |
|
exp −i |
|
t ϕ , |
(48.17) |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
так что плотность вероятности равна ϕϕ и, следовательно, от времени не зависит. Состояния, описанные функциями (48.13) называют стационарными.
25
В квантовой механике состояние частиц задается волновой функцией. Если известна волновая функция в начальный момент времени и силовое поле, то, решив уравнение Шредингера, найдем ψ в следующий момент времени.
Сущность причинности в квантовой механике: ψ0 - причина, ψ - ?
Состояние системы микрочастиц в квантовой механике однозначно вытекает из предшествующего состояния. В классической механике состояние частиц (материальных точек) определяется заданием положения и скорости частицы. Если известно состояние в начальный момент времени (xo, Po, или xo и vo) и силовое поле, в котором находится частица, то, решив его, получим положение частицы и скорость в любой последующий момент времени. В этом состоит сущность причинности в классической механике.
F = m a для квантовой механики классическое понятие состояния лишено смысла, т. к. одновременно не могут быть определены скорость и координата частицы. Но состояние частицы в квантовой механике задается волновой функцией. Следовательно, если известно ψo (x, y, z, t) в начальный момент времени и силовое поле, то из решения уравнения Шредингера получим значение волновой функции в последующий момент времени.
Квантовая механика не отменяет принцип причинности, она лишь придает ему другую форму, соответствующую истинной природе вещей.
§49. Прохождение частиц через потенциальный барьер
Различие в поведении классической и квантовой частиц отчетливо проявляется в тех случаях, когда на их пути встречается потенциальный барьер.
U
E2
U0
E1
x
0
Рис. 49.1
Пусть движется вдоль оси x. Uo - высота потенциального барьера Потенциальная энергия частицы
при x>0 - Uo, при x < 0 U = 0;
Рассмотрим поведение классической частицы (частицы, подчиняющейся законам классической механики).
Если полная энергия частицы E < Uo , частица отразится от барьера и полетит в противоположную сторону с той же энергией.
Если Е2 < Uo , частица пройдет над барьером, потеряв лишь часть своей скорости, и будет двигаться в прежнем направлении.
Поведение квантовой частиц выглядит совершенно по-другому.
Если E < U , то квантовая частица проникает в барьер на некоторую глубину и лишь затем поворачивает обратно.
Глубиной проникновения Xe будем называть расстояние, на котором вероятность обнаружения частицы уменьшается в e раз. (На границе барьера X = 0).
26
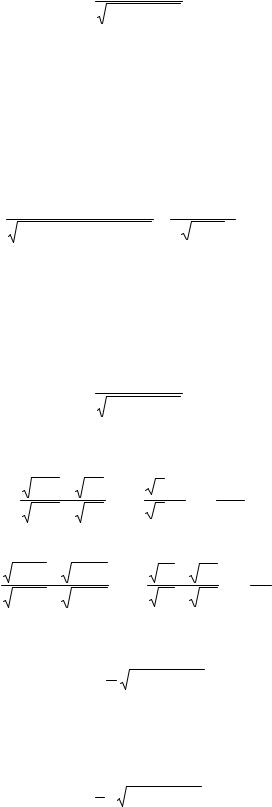
xe = |
. |
(49.1) |
8m(U0 |
− E) |
|
Теоретический расчет дает формулу (49.1).
Знаменатель этого выражения будет тем меньше, чем меньше m и чем меньше (Uo - E), но тем на большую глубину проникает частица в процессе отражения.
Пусть свободный электрон движется в металле: металл представляет для электрона потенциальную яму глубиной Uo. Электрон, двигаясь к поверхности металла, натыкается на ступен-
чатый потенциальный барьер высотой Uo. Для наиболее быстрых электронов: Uo - E = 1эв = 1.6
·10-15 Дж
Тогда
x = |
|
|
|
1,05 10−39 |
≈10−10 м; |
e |
8 |
9,1 10−31 |
1,6 10−19 |
10−48 |
|
|
|
Т.е. свободные электроны вылетают за пределы металла на расстояние ~ 10-10м, а затем возвращаются в металл.
Металл оказывается окруженным электронным облаком.
В случае же если E > U , то квантовая частица не обязательно проникает в область x < 0, и движется в первоначальном направлении. Имеется вероятность того, что частица отразится от барьера и полетит в обратном направлении
|
|
|
|
xe = |
8m(U0 |
, |
|
|
|
|
|
(49.2) |
|||
|
|
|
|
|
|
− E) |
|
|
|
|
|
|
|
||
вероятность отражения квантовой частицы. |
|
|
|
|
|
|
|
|
|
|
|||||
Если 2U0 = E, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2U0 |
− |
U0 |
2 |
|
2 −1 |
2 |
= |
0,16 |
≈ 0,03 |
||||
R = |
|
|
|
|
|
= |
|
|
|
|
|
||||
|
|
2U0 |
+ |
U0 |
|
|
2 +1 |
|
|
|
5,8 |
|
|
||
|
|
|
|
|
|
|
|
|
|||||||
Если E = 1,1U0, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,1U0 |
− |
|
0,1U0 |
2 |
|
1,1 − |
|
0,1 |
2 |
= |
0,6 |
≈ 0,3 |
||
R = |
|
|
|
|
|
|
= |
|
|
|
|
|
|
||
|
1,1U0 |
+ |
|
0,1U0 |
|
|
1,1 + |
|
0,1 |
|
|
1,8 |
|
||
|
|
|
|
|
|
|
|
||||||||
Если частица, квантовая, проходит сквозь прямоугольный барьер конечной ширины, то коэффициент прозрачности D округляется формулой:
D exp − l |
8m(U0 |
− E) . |
(49.3) |
|
|
|
|
Т.е. вероятность прохождения частицы сквозь потенциальный барьер зависит от ширины барьера l и от (Uo - E). С увеличением ширины D резко уменьшается.
Для потенциального барьера произвольной формы
|
l b |
8m(U0 |
|
, |
(49.4) |
D exp − |
∫ |
− E)dx |
|||
|
a |
|
|
|
|
где U = U(x).
27