
- •Раздел 1. Основные понятия
- •1.1. Общие сведения о сопротивлении материалов
- •1.2. Изучаемые объекты
- •1.3. Расчетные схемы элементов реальных конструкций
- •1.4. Место курса "Сопротивление материалов" в общем цикле дисциплин о механике деформирования упругих тел и образованных из них структур
- •1.5. Нагрузки и их классификация
- •1.6. Внутренние силы
- •1.7. Метод сечений
- •1.8. Основные виды деформаций бруса
- •1.9. Опоры, связи и их классификация
- •1.10. Статически определимые и статически неопределимые балки
- •1.11. Определение реакций в опорных связях
- •1.12. Эпюры внутренних сил и моментов.
- •1.13. Правила построения эпюр внутренних силовых факторов
- •Раздел 2. Теория напряженного состояния
- •2.1. Напряжения
- •2.2. Связь между напряжениями и внутренними усилиями
- •2.3. Виды напряженного состояния
- •2.4. Плоское напряженное состояние
- •2.5. Главные напряжения. Главные площадки
- •2.6. Экстремальные касательные напряжения. Площадки сдвига
- •3.1. Деформации, перемещения
- •3.2. Зависимости между деформациями и перемещениями. Формулы Коши
- •3.3. Основные гипотезы
- •3.4. Кинематические соотношения при изгибе
- •3.5. Экспериментальное изучение механических характеристик материалов при растяжении-сжатии
- •3.6. Испытания материала на растяжение
- •3.7. Определения основных механических характеристик материалов
- •Раздел 5. Уравнения равновесия балки
- •5.1. Уравнения равновесия балки в усилиях
- •5.2. Некоторые особенности эпюр перерезывающих сил и изгибающихмоментов
- •5.3. Уравнения равновесия балки в перемещениях
- •5.4. Ось стержня
- •5.5. Граничные условия
- •5.6. Растяжение и сжатие
- •5.7. Сдвиг. Чистый сдвиг
- •5.8. Деформация при сдвиге. Закон Гука при сдвиге
- •5.9. Кручение
- •Раздел 6. Геометрические характеристики плоских однородных сечений
- •6.1. Cтатический момент инерции сечения
- •6.2. Осевой момент инерции сечения
- •6.5.2. Треугольное сечение
- •6.5.3. Сечение в форме круга
- •6.6. Изменение моментов инерции при параллельном переносе осей
- •6.7. Изменение моментов инерции при повороте осей
- •6.8. Главные моменты инерции. Главные оси инерции
- •6.9. Вычисление моментов инерции сложных сечений
- •Раздел 7. Прямой изгиб
- •7.1. Прямой чистый изгиб
- •7.2. Прямой поперечный изгиб
- •7.3. Формула д.И. Журавского
- •7.4. Расчеты на прочность при изгибе
- •7.5. Балки постоянного поперечного сечения из пластичных материалов
- •7.6. Балки постоянного поперечного сечения из хрупких материалов
- •7.7. Балки переменного поперечного сечения
- •7.8. Определение перемещений в балках постоянного сечения методом непосредственного интегрирования уравнений равновесия
- •7.9. Определение перемещений в балках постоянного сечения методом начальных параметров
- •Раздел 8. Критерии прочности
- •8.1. Основные теории прочности
- •8.1.1. Первая теория прочности, или теория наибольших нормальных напряжений (теория Галилея-Ренкина)
- •8.1.2 Вторая теория прочности, или теория наибольших линейных деформаций (теория Мариотта-Грасгофа, 1862 г.)
- •8.1.3. Третья теория прочности, или теория наибольших касательных напряжений (теория Кулона, 1772 г.)
- •8.1.4. Четвертая (энергетическая) теория прочности, или теория удельной потенциальной энергии формоизменения (Теория Губера-Мизеса-Генки, 1904 г.)
- •8.1.5. Единая теория прочности
- •8.2. Понятия о некоторых новых теориях прочности
- •8.2.1. Критерий прочности Ягна-Бужинского
- •8.2.2. Критерий прочности Писаренко-Лебедева
- •Раздел 9. Сложное сопротивление
- •9.1. Общие положения
- •9.2. Изгиб с кручением брусьев круглого сечения
- •9.3. Эквивалентные напряжения по различным теориям прочности
- •Раздел 10. Расчет конструкций по предельным состояниям
- •10.1. Основные понятия о предельном состоянии
- •10.2. Расчеты при растяжении и сжатии
- •10.3. Расчеты при кручении
- •10.4. Расчеты при изгибе
Раздел 2. Теория напряженного состояния
2.1. Напряжения
Внутренние силы так же, как и внешние нагрузки, распределенные по поверхности, характеризуются интенсивностью (рис. 2.1), которая равна
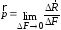
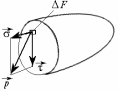
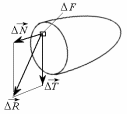
Рис. 2.1
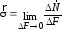 -
интенсивность нормальных сил - нормальные
напряжения,
вызывающие отрыв (сжатие) частиц
(размерность
-
интенсивность нормальных сил - нормальные
напряжения,
вызывающие отрыв (сжатие) частиц
(размерность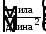 ).
).
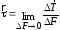 -
интенсивность касательных сил -
касательные напряжения,
вызывающие сдвиг (размерность
-
интенсивность касательных сил -
касательные напряжения,
вызывающие сдвиг (размерность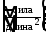 ).
).
Нормальные и касательные напряжения
являются составляющими полного
напряжения
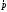 в точке по данному сечению, величина
которого вычисляется по формуле
в точке по данному сечению, величина
которого вычисляется по формуле .
.
Величины нормальных и касательных напряжений в каждой точке элемента зависят от направления сечения, проходящего через эту точку.
Совокупность нормальных и касательных напряжений, действующих по различным площадкам, проходящим через рассматриваемую точку, представляют собой напряженное состояние в этой точке.
2.2. Связь между напряжениями и внутренними усилиями
Рассмотрим элементарную площадку
dF поперечного сеченияF(сечения,
нормального к осиx) бруса с
действующими по этой
площадке нормальными и касательными
и касательными напряжениями (рис. 2.2). Разложим
напряжения
напряжениями (рис. 2.2). Разложим
напряжения на составляющие
на составляющие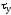 и
и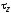 ,
параллельные соответственно
осямyиz. На площадку
,
параллельные соответственно
осямyиz. На площадку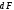 действуют элементарные силы
действуют элементарные силы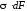 ,
,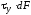 ,
,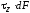 ,
параллельные соответственно
осямx, y иz. Проекции
всех элементарных сил (действующих
на всех элементарных площадкахdF сеченияF) на осиx, y иzи их моменты относительно
этих осей определяются
выражениями
,
параллельные соответственно
осямx, y иz. Проекции
всех элементарных сил (действующих
на всех элементарных площадкахdF сеченияF) на осиx, y иzи их моменты относительно
этих осей определяются
выражениями
 ;
;
(2.1)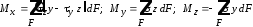 .
.
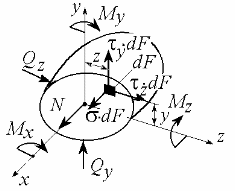
В левых частях выражений (2.1) указаны
внутренние усилия, действующие
в поперечном сечении бруса и приведенные
к точке пересечения оси xи
поперечного сечения. А именно:N-
продольная сила;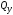 и
и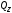 - поперечные силы, параллельные
соответственно осямyиz;
- поперечные силы, параллельные
соответственно осямyиz;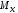 - крутящий момент;
- крутящий момент;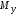 - изгибающий момент относительно осиy(действующий в плоскостиxz);
- изгибающий момент относительно осиy(действующий в плоскостиxz);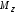 - изгибающий момент относительно
осиz(действующий в
плоскостиxy).
- изгибающий момент относительно
осиz(действующий в
плоскостиxy).
2.3. Виды напряженного состояния
Совокупность нормальных и касательных напряжений, действующих по всем площадкам, проходящим через рассматриваемую точку, называется напряженным состоянием в этой точке.
Различают следующие виды напряженного состояния:
а) пространственное (трехосное) напряженное состояние (рис. 2.3, а), когда через рассматриваемую точку тела нельзя провести ни одной площадки, в которой касательные и нормальные напряжения были бы равны нулю;
б) плоское (двухосное) напряженное состояние (рис. 2.3, б), когда в одной (и только одной) площадке, проходящей через рассматриваемую точку тела, касательные и нормальные напряжения равны нулю;
в) линейное (одноосное) напряженное состояние (рис. 2.3, в), когда касательные и нормальные напряжения в двух площадках, проходящих через рассматриваемую точку тела, равны нулю.
а)б)в)

Рис. 2.3
2.4. Плоское напряженное состояние
При плоском напряженном состоянии, как отмечалось выше, в одной из площадок, проходящих через рассматриваемую точку, касательные и нормальные напряжения равны нулю.
Выделим из тела в окрестности этой точки
бесконечно малую (элементарную)
треугольную призму и совместим
эту площадку с плоскос-тью чертежа.
Индекс у нормальных и касательных
напряжений (рис.2.4, а) указывает на
направление их действия. Например,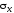 - напряжение, действующее на
площадке, перпендикулярной осиx, в
направлении осиx.
- напряжение, действующее на
площадке, перпендикулярной осиx, в
направлении осиx.
Нормальные напряжения по боковой грани
призмы, наклоненной под углом
 к грани, по которой действуют напряжения
к грани, по которой действуют напряжения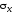 ,
обозначим
,
обозначим ,
а касательные напряжения по этой грани
,
а касательные напряжения по этой грани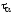 .
.
а)б)
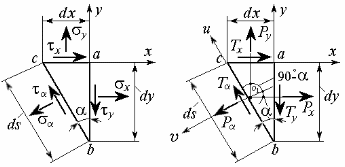
Рис. 2.4
Умножив каждое из действующих напряжений (рис. 2.4, а) на площадь грани, по которой оно действует, получим систему сосредоточенных сил, приложенных в центрах тяжести соответствующих граней (рис. 2.4,б):
(2.2)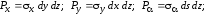
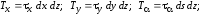
В силу того, что выделенный элемент находится в равновесии, для него справедливы следующие уравнения статики :
(2.3) ;
;
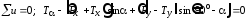 ;
;
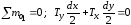 .
.
Подставив в последнее уравнение выражения
для сил
 и
и из (2.2), получим
из (2.2), получим
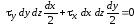 ,
,
откуда
(2.4) .
.
Выражение (2.4) представляет собой математическую запись закона парности касательных напряжений, который гласит, что касательные напряжения по двум взаимно перпендикулярным площадкам, перпендикулярные к их общему ребру, равны по абсолютной величине и направлены либо оба к ребру, либо оба от ребра (рис. 2.5).
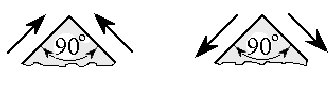
Рис. 2.5
Первые два уравнения из (2.3) с учетом выражений для усилий из (2.2) принимают вид:
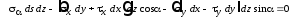 ;
;
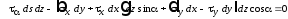 .
.
Учитывая, что
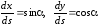 ,
сократим данные уравнения на произведение
,
сократим данные уравнения на произведение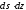 .
В результате получим:
.
В результате получим:
 ;
;
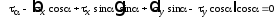 .
.
Используя закон парности касательных напряжений (2.4), получим:
 ,
,
(2.5)
(2.6) .
.
При выводе формул (2.5), (2.6) учтена
тригонометрическая
зависимость
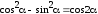 .
.
Формулы (2.5), (2.6) позволяют определять
значения нормальных и касательных
напряжений в любых площадках, проходящих
через данную точку, если известны
напряжения
 и
и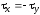 в любых двух проходящих через
нее взаимно перпендикулярных площадках.
в любых двух проходящих через
нее взаимно перпендикулярных площадках.
По формуле (2.5) вычислим сумму нормальных
напряжений в двух взаимно перпендикулярных
площадках, для одной из которых угол
 равен
равен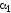 ,
а для другой
,
а для другой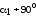 :
:

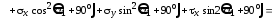
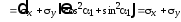 ,
,
т. е.
(2.7)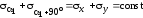 .
.
Таким образом, сумма величин нормальных напряжений в двух взаимно перпендикулярных площадках есть величина постоянная. Следовательно, если в одной из таких площадок нормальные напряжения имеют максимальное значение, то в другой - минимальное.
При выводе формулы (2.7) были использованы следующие тригонометрические зависимости:
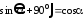 ,
, ,
,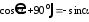 ,
,
 ,
, .
.
