
- •Раздел 1. Основные понятия
- •1.1. Общие сведения о сопротивлении материалов
- •1.2. Изучаемые объекты
- •1.3. Расчетные схемы элементов реальных конструкций
- •1.4. Место курса "Сопротивление материалов" в общем цикле дисциплин о механике деформирования упругих тел и образованных из них структур
- •1.5. Нагрузки и их классификация
- •1.6. Внутренние силы
- •1.7. Метод сечений
- •1.8. Основные виды деформаций бруса
- •1.9. Опоры, связи и их классификация
- •1.10. Статически определимые и статически неопределимые балки
- •1.11. Определение реакций в опорных связях
- •1.12. Эпюры внутренних сил и моментов.
- •1.13. Правила построения эпюр внутренних силовых факторов
- •Раздел 2. Теория напряженного состояния
- •2.1. Напряжения
- •2.2. Связь между напряжениями и внутренними усилиями
- •2.3. Виды напряженного состояния
- •2.4. Плоское напряженное состояние
- •2.5. Главные напряжения. Главные площадки
- •2.6. Экстремальные касательные напряжения. Площадки сдвига
- •3.1. Деформации, перемещения
- •3.2. Зависимости между деформациями и перемещениями. Формулы Коши
- •3.3. Основные гипотезы
- •3.4. Кинематические соотношения при изгибе
- •3.5. Экспериментальное изучение механических характеристик материалов при растяжении-сжатии
- •3.6. Испытания материала на растяжение
- •3.7. Определения основных механических характеристик материалов
- •Раздел 5. Уравнения равновесия балки
- •5.1. Уравнения равновесия балки в усилиях
- •5.2. Некоторые особенности эпюр перерезывающих сил и изгибающихмоментов
- •5.3. Уравнения равновесия балки в перемещениях
- •5.4. Ось стержня
- •5.5. Граничные условия
- •5.6. Растяжение и сжатие
- •5.7. Сдвиг. Чистый сдвиг
- •5.8. Деформация при сдвиге. Закон Гука при сдвиге
- •5.9. Кручение
- •Раздел 6. Геометрические характеристики плоских однородных сечений
- •6.1. Cтатический момент инерции сечения
- •6.2. Осевой момент инерции сечения
- •6.5.2. Треугольное сечение
- •6.5.3. Сечение в форме круга
- •6.6. Изменение моментов инерции при параллельном переносе осей
- •6.7. Изменение моментов инерции при повороте осей
- •6.8. Главные моменты инерции. Главные оси инерции
- •6.9. Вычисление моментов инерции сложных сечений
- •Раздел 7. Прямой изгиб
- •7.1. Прямой чистый изгиб
- •7.2. Прямой поперечный изгиб
- •7.3. Формула д.И. Журавского
- •7.4. Расчеты на прочность при изгибе
- •7.5. Балки постоянного поперечного сечения из пластичных материалов
- •7.6. Балки постоянного поперечного сечения из хрупких материалов
- •7.7. Балки переменного поперечного сечения
- •7.8. Определение перемещений в балках постоянного сечения методом непосредственного интегрирования уравнений равновесия
- •7.9. Определение перемещений в балках постоянного сечения методом начальных параметров
- •Раздел 8. Критерии прочности
- •8.1. Основные теории прочности
- •8.1.1. Первая теория прочности, или теория наибольших нормальных напряжений (теория Галилея-Ренкина)
- •8.1.2 Вторая теория прочности, или теория наибольших линейных деформаций (теория Мариотта-Грасгофа, 1862 г.)
- •8.1.3. Третья теория прочности, или теория наибольших касательных напряжений (теория Кулона, 1772 г.)
- •8.1.4. Четвертая (энергетическая) теория прочности, или теория удельной потенциальной энергии формоизменения (Теория Губера-Мизеса-Генки, 1904 г.)
- •8.1.5. Единая теория прочности
- •8.2. Понятия о некоторых новых теориях прочности
- •8.2.1. Критерий прочности Ягна-Бужинского
- •8.2.2. Критерий прочности Писаренко-Лебедева
- •Раздел 9. Сложное сопротивление
- •9.1. Общие положения
- •9.2. Изгиб с кручением брусьев круглого сечения
- •9.3. Эквивалентные напряжения по различным теориям прочности
- •Раздел 10. Расчет конструкций по предельным состояниям
- •10.1. Основные понятия о предельном состоянии
- •10.2. Расчеты при растяжении и сжатии
- •10.3. Расчеты при кручении
- •10.4. Расчеты при изгибе
6.2. Осевой момент инерции сечения
Осевым моментом инерции плоского сечения относительно какой-либо оси, лежащей в той же плоскости, называется сумма произведений элементарных площадок dFна квадраты их расстояний до данной оси.
(6.5)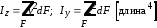 ,
,
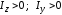 .
.
6.3. Полярный момент инерции сечения
Полярным моментом инерции плоского
сечения
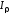 относительно какого-либо
полюсао
(рис. 6.1), лежащего в плоскости сечения,
называется сумма произведений
элементарных площадокdFна квадраты
их расстояний
относительно какого-либо
полюсао
(рис. 6.1), лежащего в плоскости сечения,
называется сумма произведений
элементарных площадокdFна квадраты
их расстояний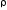 до полюса:
до полюса:
 ,
,
а
так как
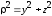 ,
то
,
то
 .
.
(6.6)
6.4. Центробежный момент инерции сечения
(6.7)
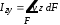
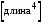 ,
,
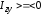 .
.
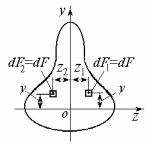
 ,
,
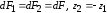 ,
,
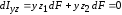 ,
,
Рис. 2.3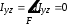 .
.
Таким образом, центробежный момент инерции сечения относительно осей, из которых одна или обе совпадают с его осями симметрии, равен нулю.
6.5. Вычисление моментов инерции сечений простой формы
6.5.1. Прямоугольное сечение
1. Осевой момент инерции прямоугольника.
Разбив прямоугольник с основанием bи высотойhна бесконечно узкие горизонтальные полоски, возьмем одну из них на расстоянииyот осиz(рис. 6.4,а). Ширина этой полоскиb, высотаdy. Момент инерции ее относительно осиzбудет равен
 .
.
Момент инерции прямоугольника
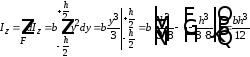 ,
,
окончательно
(6.8)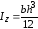 .
.
Очевидно, что момент инерции прямоугольника относительно оси y
(6.9)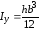 .
.
Приняв b=h=a, получим формулу для определения момента инерции квадратного сечения со сторонойa:
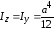 .
.
2. Центробежный момент инерции прямоугольника.
Выделим элементарную площадку dF = (рис. 6.4,б).
(рис. 6.4,б).
Вначале вычислим центробежный момент
инерции не всего прямоугольника,
а лишь вертикальной полоски высотой hи шириной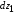 ,
расположенной на расстоянии
,
расположенной на расстоянии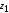 от оси
от оси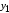 :
:
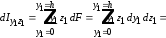
(6.10)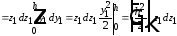 .
.
а) б)
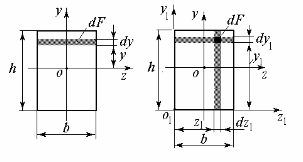
Рис. 6.4
В выражении (6.10)
 вынесено за знак интеграла, так как для
всех площадок, принадлежащих
рассматриваемой вертикальной полоске,
оно постоянно.
вынесено за знак интеграла, так как для
всех площадок, принадлежащих
рассматриваемой вертикальной полоске,
оно постоянно.
 .
.
(6.11)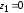 до
до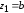
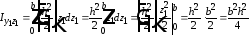 ;
;
 .
.
(6.12)
(6.13)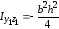 .
.
Центробежные моменты инерции
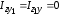 ,
,
так
как оси
 и
и проходят через центр тяжести сечения.
проходят через центр тяжести сечения.
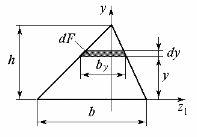
6.5.2. Треугольное сечение
Определим осевой момент инерции
треугольника относительно оси
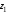 (рис. 6.5).
(рис. 6.5).
 ,
,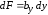 ,
,
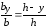 ,
,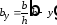 .
.

Рис. 6.5
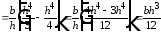 ;
;
 .
.
(6.14)
6.5.3. Сечение в форме круга
1. Полярный момент инерции круга (рис. 6.6).

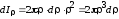 ;
;
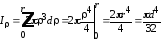 ;
;
(6.15)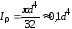 ,
,
где
 - диаметр круга.
- диаметр круга.
Рис. 6.6
2. Осевой момент инерции круга.
Ввиду симметрии круга относительно
любого диаметра (рис. 6.6) осевые
моменты инерции относительно любых
осей, проходящих через центр круга,
равны между собой. Поэтому
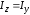 ,
а так как
,
а так как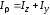 ,
то величина осевого момента инерции
площади круга относительно любой
оси, проходящей через центр круга, равна
половине полярного момента инерции,
т. е.
,
то величина осевого момента инерции
площади круга относительно любой
оси, проходящей через центр круга, равна
половине полярного момента инерции,
т. е.
(6.16)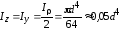 .
.
3. Осевой момент инерции кругового кольца.
Это разность осевых моментов инерции большого круга диаметром Dи малого круга диаметромd.
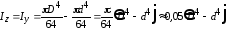 ;
;
(6.17) .
.
