
- •Сыктывкарский государственный университет
- •1. Контрольные задания 4
- •Задание 1. Задача о выпуске продукции при ограниченных ресурсах.
- •Задание 2. Классическая транспортная задача.
- •2. Методические указания по выполнению контрольных заданий Задача о выпуске продукции при ограниченных ресурсах.
- •Классическая транспортная задача.
- •Задача об аренде оборудования.
- •3. Пример решения классической транспортной задачи.
- •Исходные данные (запасы, потребности и цены)
- •Начальный план
- •Значения оценок
- •План грузоперевозок
- •Новый план грузоперевозок
- •2 Этап.
- •Значения оценок
- •План грузоперевозок
- •Новый план грузоперевозок
- •3 Этап.
- •Значения оценок
- •План грузоперевозок
- •Новый план грузоперевозок
- •4 Этап.
- •Значения оценок
- •План грузоперевозок
- •Новый план грузоперевозок
- •5 Этап.
- •Значения оценок
- •Оптимальный план грузоперевозок
- •4. Задача об аренде оборудования Планы аренды. Постановка задачи.
- •Сетевая модель задачи и ее решение.
- •Табличный метод решения задачи.
- •Рекомендуемый библиографический список
- •Приложение. Бесконтурные сети
- •Неправильная нумерация Правильная нумерация(1 и 2, 4 и 5 можно поменять местами) Рис. 2.
Табличный метод решения задачи.
Исходная таблица стоимостей аренды равнозначна сетевой модели, поэтому потенциалы Vi и оптимальные планы аренды можно найти непосредственно в таблице, не изображая сеть, тем более, что при большихNсеть становится громоздкой.
Потенциалы Vi
рассчитываем, как и выше – начиная
сi=Nпо формуле
![]() ,
записывая их в дополнительном столбце
таблицы стоимостейпоследовательно
снизу вверх. Клетки (i,j),
для которых достигается минимум в
формуле
,
записывая их в дополнительном столбце
таблицы стоимостейпоследовательно
снизу вверх. Клетки (i,j),
для которых достигается минимум в
формуле
![]() ,
выделяем каким-либо образом. Таким
образом. В каждой строчке таблицы будетне менееодной выделенной клетки.
,
выделяем каким-либо образом. Таким
образом. В каждой строчке таблицы будетне менееодной выделенной клетки.
По выделенным
клеткам находим оптимальные планы
аренды. Для этого в первой строчке
найдем выделенную клетку (1,i1)
с номером выделенного столбцаi1
. Затем найдем в строкеi1
выделенную клетку (i1,i2)
с номером выделенного столбцаi2
и так далее. Получим оптимальный
план аренды![]() .
Другие планы, если они есть, находятся
аналогично.
.
Другие планы, если они есть, находятся
аналогично.
Рассмотрим снова пример2и получим следующую таблицу.
|
i |
2 |
3 |
4 |
5 |
6 |
7 |
Vi
|
|
1 |
49 |
99 |
145 |
197 |
244 |
296 |
288 |
|
2 |
– |
50 |
96 |
146 |
198 |
247 |
239 |
|
3 |
– |
– |
48 |
95 |
147 |
189 |
189 |
|
4 |
– |
– |
– |
49 |
98 |
148 |
148 |
|
5 |
– |
– |
– |
– |
51 |
101 |
101 |
|
6 |
– |
– |
– |
– |
– |
53 |
53 |
|
7 |
|
|
|
|
|
|
0 |
В этой таблице выделены следующие клетки:
(6,7),.так как V6 = C6,7+V7 = 53;
(5.7), так как V5 = C5,7+V7 = 101
(4,7),.так как V4 = C4,7+V7 = 148
(3,7), так как V3 = C3,7 +V7= 189
(2,3), так как V2 = C2,3 + V3 = 239
(1,2) и (1,3), так как V1 = C1,2 + V2 = С1,3 + V3 = 288.
Последовательность выделенных клеток (1,2), (2,3),(3,7) дает оптимальный план аренды (1, 2, 3, 7), а последовательность выделенных клеток(1, 3) и(3,7) дает оптимальный план аренды (1, 3, 7). Стоимость оптимальных планов равна 288 у. е. (первая строка, дополнительный столбец).
Рекомендуемый библиографический список
Основная литература
Никитенков В.Л. Холопов А.А. Задачи линейного программирования и методы их решения. Уч. пособие. Сыктывкар: Изд-во СыктГУ, 2008, 268с. Электронная версия есть на сервере СыктГУ, лаборатория №2 , Учебные материалы \ Кафедра ГАМС \ Математическое программирование и ИО
Грызина Н. Ю.Математические методы исследования операций в экономике. Учебно-методический комплекс - М.: Евразийский открытый институт. 2009. 204c. Эл. библиотека «Онлайн». (Электронная версия есть в методическом кабинете финансово-экономического факультета)
Дополнительная литература
Юденков А. М. Математическое программирование в экономике. Рек.УМО - Москва: Финансы и статистика, 2010. (ЭБС)
Хазанова Л.Э. Математическое моделирование в экономике. М.: БЕК, 2002, 133с.
Приложение. Бесконтурные сети
Сети являются частным случаем графов. Ограничимся случаем бесконтурных сетей, используемых в задачах контрольных заданий.
Графявляется математическим, формальным представлением объектов, между которыми попарно установлены некоторые связи [1,2,4]. Объекты называютсявершинами и графически изображаются кружками. Связи считаются установленными междунекоторыми парамиизразличныхвершин и считаются односторонними. Графически связь изображается линией со стрелкой, илидугой,соединяющей две вершины. Согласно направлению связи, т.е. направлению стрелки, соединяемые вершины являютсяначалом иконцомдуги, или, другими словами, начальной и конечной вершинами дуги.
Будем считать, что между двумя вершинами есть не более одной дуги (нет "параллельных" дуг). Формально этого можно добиться, разбив дугу на две с помощью промежуточной вершины. В дальнейшем дугу будем записать в виде упорядоченной пары (a,b), гдеa– начало дуги,b– конец дуги.
Путём
из вершины![]() в вершину
в вершину![]() ,
или путём, начинающимся в
,
или путём, начинающимся в![]() и заканчивающимся в
и заканчивающимся в![]() ,
называется последовательность вершин
,
называется последовательность вершин![]() ,
где пары
,
где пары![]() ,
,![]() ,
…,
,
…,![]() являются дугами. Графически путь
представляет непрерывную направленную
линию из дуг, согласованную с направлениями
стрелок ("движения по стрелкам").
Если
являются дугами. Графически путь
представляет непрерывную направленную
линию из дуг, согласованную с направлениями
стрелок ("движения по стрелкам").
Если![]() ,
т.е. если начало пути совпадает с концом
пути, то путь называетсяконтуром.Цепочкой
из вершины
,
т.е. если начало пути совпадает с концом
пути, то путь называетсяконтуром.Цепочкой
из вершины![]() в вершину
в вершину![]() называется последовательность
называется последовательность![]() из различных вершин, в которой дугами
являются
из различных вершин, в которой дугами
являются![]() или
или![]() ,
,![]() или
или![]() ,
и т.д. Таким образом, цепочка соответствует
линии из
,
и т.д. Таким образом, цепочка соответствует
линии из![]() в
в![]() без учёта направления стрелок. Замкнутая
цепочка называетсяциклом.
без учёта направления стрелок. Замкнутая
цепочка называетсяциклом.
Будем предполагать, что любые две вершины можно соединить цепочкой (соответствующий граф называется связным).
|
|
( a,c,b,d,f ) – путь ( b,d,f,c,b ) – контур ( a,b,c,f ) – цепочка ( a, b, c, a ) – цикл |
Определение. Конечная совокупность вершин и дуг (и их графическое изображение) называетсясетью, если выполняются условия:
а) связности;
б) отсутствия петель (начало и конец дуги различны);
в) отсутствие параллельных дуг.
Определение.Сеть называетсябесконтурной, илиупорядоченнойсетью, если в ней нет контуров.
Замечание. В литературе встречается также терминациклическая сеть.
Сеть на рис.1 не является бесконтурной, т.к. есть контур (b,d,f,c,b).
Н у м е р а ц и я вершин сети – это сопоставление вершинам номеров – натуральных чисел, при этом различным вершинам сопоставляются различные номера.
Определение. Нумерация называетсяправильной, если:
а) номера идут подряд: 1, 2, …, m, гдеm – число вершин;
б)
номер начала дуги меньшеномера конца дуги, т.е. все дуги
записываются в виде![]() ,
где
,
где![]() .
.
В сетях, имеющих контур,
правильной нумерации не может быть,
так как для вершины контура с номером
n получаем
противоречивое неравенство![]() .
.
В бесконтурных сетях правильная нумерация возможна и может быть проставлена по следующей процедуре (алгоритм Форда).
1.Найдём вершину, которая не является началом никакой дуги, т.е. из которой дуги не выходят. Такая вершина легко может быть найдена, если, начиная с любой вершины, двигатьсяпо стрелкам дуг, переходя из вершины в вершину.
2.Присвоим найденной вершине текущий номер. Первый раз таким номером являетсяm– число вершин сети.
3.Уменьшим текущий номер на одну единицу. Вычеркнем или пометим как-либо дуги,заканчивающиеся в вершине, только что пронумерованной. В дальнейшем считаем, что этих дуг нет в сети. Возвращаемся к шагу 1, т.е. все повторяем с начала.
Замечание. 1. Если не удаётся найти вершину в шаге 1, то в сети есть контур и правильная нумерация невозможна, так что алгоритм Форда является проверкой, будет ли сеть бесконтурной.
2. Правильных нумераций в сети может быть несколько.
Пример 2.

 J
J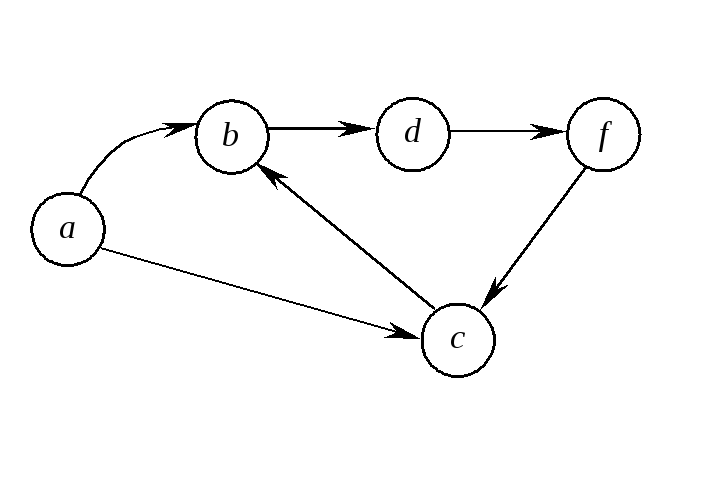 Рис.
1
Рис.
1