
линал
.pdfвыполняться тождественно (как равенство между векторами в V ). Следовательно, допущение, что линейная комбинация векторов e1,e2,...,en+1 с коэффициентами l1,l2,...,ln+1 равна нулевому
вектору q , влечет l1 = l2 = ... = ln+1 = 0 , а это означает, что e1,e2,...,en+1 линейно независимы. Пусть Pn (x) = a0 + a1x + ...+ an xn - произвольный многочлен степени £ n . В последней записи Pn (x) представлен в виде линейной комбинации векторов e1,e2,...,en+1 , что вместе с линейной независимостью этих векторов доказывает, что система e1,e2,...,en+1 - базис в пространстве многочленов степени £ n
15.Базис линейного пространства. Единственность разложения вектора по базису.
Определение. Система векторов e1,e2,...,en линейного пространства V называется базисом в V , если: 1) e1,e2,...,en линейно независима; 2) "x Î V $l1,l2,...,ln (вещественные числа):
x = l1e1 + l2e2 + ...+ lnen .Правая часть равенства называется разложением вектора x по базису
e1,e2,...,en , а числа l1,l2,...,ln - координатами вектора x в базисе e1,e2,...,en . Теорема. Пусть V -
линейное пространство, |
e1,e2,...,en |
- |
|
базис в V , x Î V . Координаты x относительно базиса |
||||||||||||||||||
определены однозначно. Доказательство. Пусть x Î V , x = a1e1 + a2e2 + ...+ anen и |
||||||||||||||||||||||
x = b1e1 + b2e2 + ...+ bnen . Имеем x + (-x) = q . С другой стороны, |
x + (-x) = (a1e1 + a2e2 + ...+ αnen ) + |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
следствие 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
из аксиом |
+(-1)×(b e |
+ b |
e |
|
+ ...+ b |
e |
|
|
) |
|
= |
|
|
|
|
|
|
|
|
||||
|
1 1 |
2 |
|
2 |
|
|
n |
|
|
n |
акс. 6 |
|
|
|
|
|
|
|
|
|||
= (a1e1 + a2e2 + ...+ anen ) + ((-1)×b1e1 + (-1)×b2e2 + ...+ (-1)bnen ) = |
|
|||||||||||||||||||||
= |
(a1e1 + a2e2 + ...+ anen ) + ((-b1e1) + (-b2e2 ) + ...+ (-bnen )) = |
|
||||||||||||||||||||
акс. 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
(a - b )e |
|
+ (a |
|
- b |
|
|
)e |
|
+ ...+ (a |
|
- b |
|
)e |
|
= q . |
|
|||||
акс. 2,5,1 1 |
1 |
1 |
|
2 |
|
|
2 |
|
|
2 |
|
|
n |
|
n |
|
n |
|
|
|||
Откуда в силу линейной независимости векторов e1,e2,...,en |
следует a1 - b1 = 0, ..., an - bn = 0 , т.е. |
|||||||||||||||||||||
a1 = b1, ..., |
an = bn .Допустив, что вектор x имеет два разложения по базису e1,e2,...,en , мы |
|||||||||||||||||||||
получили, что эти разложения совпадают, это и означает, что координаты вектора x |
||||||||||||||||||||||
относительно базиса e1,e2,...,en |
определены однозначно. Теорема доказана. |
|||||||||||||||||||||
16.Базис линейного пространства. Координаты суммы векторов и произведения вектора на число.
Определение. Система векторов e1,e2,...,en линейного пространства V называется базисом в V ,
если: 1) e1,e2,...,en |
линейно независима; 2) "x Î V |
$l1,l2,...,ln |
(вещественные числа): |
|
|
|
|
||||||||||||||||||||||||||||||||||
x = l1e1 + l2e2 + ...+ lnen .Правая часть равенства называется разложением вектора x по базису |
|||||||||||||||||||||||||||||||||||||||||
e1,e2,...,en , а числа l1,l2,...,ln |
- координатами вектора x в базисе e1,e2,...,en . Теорема. Пусть V - |
||||||||||||||||||||||||||||||||||||||||
линейное пространство, e1,e2,...,en |
|
- |
базис в V . При сложении любых двух векторов их |
|
|
||||||||||||||||||||||||||||||||||||
соответствующие координаты складываются, при умножении вектора на число каждая |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
координата умножается на это число. Доказательство. (Вместо a,b,c писать нужно |
2 |
|
) |
|
|||||||||||||||||||||||||||||||||||||
e1,e2,...,en )Пусть d1 = l1a + m1b + n1c , |
d2 = l2a + m2b + n2c . |
1 |
|
2 |
|
( |
1 |
1 |
|
1 ) |
( |
2 |
|
2 |
|
|
|
||||||||||||||||||||||||
|
( 1 |
2 |
|
) |
( 1 |
2 |
|
) |
( 1 |
|
2 |
|
) . |
|
1 |
|
2 |
|
( 1 |
2 ) |
|
( |
d + d |
|
= |
l a |
+ m b + n c |
+ l |
|
a + m |
b + n |
|
c |
|
= |
||||||
|
|
|
|
|
|
|
|
|
1 |
2 ) |
|
|
( 1 |
|
2 ) |
|
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||
= |
l a + l |
|
a |
|
+ m b + m |
b |
|
+ n c + n |
|
c |
|
d |
+ d |
|
= |
l + l |
|
a + |
m + m |
|
|
b |
+ |
n + n |
|
c |
|
|
|
|
|
|
|
|
|
|
|||||
В силу теоремы о единственности разложения вектора по базису числа (l1 + l2 ) , |
(m1 + m2 ) , |
(n1 + n2 ) |
|||||||||||||||||||||||||||||||||||||||
и являются координатами вектора d1 + d2 .Пусть k – произвольное вещественное число, d1 – вектор, введенный выше. Рассмотрим вектор k d1 . Имеем k d1 = k (l1a + m1b + n1c) .
Используя свойство 3, а затем 5 умножения вектора на число, получим
k d1 = k (l1a) + k (m1b) + k (n1c) = (kl1 )a + (km1 )b + (kn1 )c .Используя теорему о единственности разложения вектора по базису, придем к тому, что числа (kl1 ) (km1 ) и (kn1 ) – координаты вектора k d1 относительно базиса a , b , c . Теорема доказана.
Created with ReaSoft PDF Printer free trial.
Purchase at http://www.reasoft.com/
17.Размерность линейного пространства.
Теорема. Пусть V - линейное пространство, e1,e2,...,en - базис в V . Всякая система s векторов x1,x2,...,xs при s > n линейно зависима. Доказательство. Достаточно доказать утверждение для s = n +1Пусть x1,x2,...,xn+1 - произвольная система векторов в V .Случай 1. Среди x1,x2,...,xn+1 есть q , следовательно, система x1,x2,...,xn+1 линейно зависима.Слу чай 2. "j, j = 1,..., n +1, x j ¹ q . Так как система e1,e2,...,en - базис, существуют такие aij i = 1,...,n +1, j = 1,...,n , что
x1 = a11e1 + a12e2 + ...+ a1,nen ,
x2 = a21e1 + a22e2 + ...+ a2,nen ,(10.4)
……………………………………
xn+1 = an+1,1e1 + an+1,2e2 + ...+ an+1,nen .
Среди чисел a11,a12,...,a1,n есть отличные от нуля (иначе x1 = q ). Не ограничивая общности рассуждений, можно считать, что a11 ¹ 0 (в противном случае можно перенумеровать базисные векторы), следовательно,
e = |
1 |
x |
- a12 e |
2 |
-...- |
a1,n |
e |
n |
.(10.5) |
|
|
||||||||
1 |
a11 |
1 |
a11 |
|
a11 |
|
|||
|
|
|
|
|
|
||||
Подставив (10.5) во все равенства (10.4), начиная со второго, получим
x2 = b21x1 + b22e2 + ...+ b2,nen ,
……………………………………(10.6)
xn+1 = bn+1,1x1 + bn+1,2e2 + ...+ bn+1,nen .
Векторы x2,..,xn+1 линейно выражаются через x1,e2,...,en . Если в первом равенстве в системе (10.6) b22 = b23 = ... = b2,n = 0 , то x2 = b21x1 , и система векторов x1,x2 линейно зависима. Тогда, согласно теореме 2, система векторов x1,x2,...,xn+1 также линейно зависима. Если же среди b22,b23,...,b2,n есть отличные от нуля, то, не ограничивая общности рассуждений, считаем, что b22 ¹ 0 .
Из первого равенства в (10.6) имеем
e |
|
= |
1 |
x |
|
- b21 x |
- b23 e |
|
-...- |
b2,n |
e |
|
.(10.7) |
|
b22 |
|
|
|
|
||||||||
|
2 |
|
|
2 |
b22 1 |
b22 |
3 |
|
b22 |
n |
|
||
Подставим (10.7) во все равенства (10.6), начиная со второго, получим выражения x3,..,xn+1 через
x1,x2,e3,...,en . Процедуру повторим n - 2 раза и придем к равенству xn+1 = g1x1 + g2x2 + ...+ gnxn . Один из векторов системы x1,x2,...,xn+1 оказался линейной комбинацией остальных, следовательно,
x1,x2,...,xn+1 линейно зависимы. Теорема доказана.
Следствие. Все базисы линейного пространства V состоят из одного и того же числа векторов. Действительно, пусть e1,e2,...,en (I) и e1¢ ,e¢2,...,e¢s (II) - два базиса в V . Допустим, s > n . Так как
система (I) - базис, то в силу теоремы 5 это означает, что система (II) линейно зависима. Это противоречит тому, что (II) - базис. Отсюда s £ n . Допустим теперь, что n > s . Так как система (II) - базис, то в силу теоремы 5 это означает, что система (I) линейно зависима. Это противоречит тому, что (I) - базис. Следовательно, n £ s . Вместе эти два заключения дают s = n . Определение. Число векторов в любом базисе линейного пространства V называется размерностью линейного пространства.Для размерности линейного пространства V принято обозначение dim V .
18.Связь между базисам линейного пространства. |
,...,en (II) - два базиса в V . Так как (I) - базис, |
||||||
Пусть V - линейное пространство, |
e1,e2,...,en (I) и e1 |
,e2 |
|||||
|
|
|
|
|
¢ |
¢ |
¢ |
любой вектор из V , в частности любой вектор системы (II), можно представить в виде линейной |
|||||||
комбинации векторов системы (I), |
т.е. найдутся такие числа tij , i, j = 1,...,n , что |
||||||
e¢ |
= t e + t |
e |
+ ...+ t |
e |
|
|
|
1 |
11 1 |
21 2 |
|
n1 n |
|
|
|
Created with ReaSoft PDF Printer free trial.
Purchase at http://www.reasoft.com/
e¢2 = t12e1 + t22e2 + ...+ tn2en
……………………………….(11.1)
e¢n = t1,ne1 + t2,ne2 + ...+ tnnen
Определение 1. Матрица T = 
 tij
tij 
 , i, j = 1,...,n называется матрицей перехода от базиса (I) к базису (II). Замечание1 . Столбцы матрицы перехода T =
, i, j = 1,...,n называется матрицей перехода от базиса (I) к базису (II). Замечание1 . Столбцы матрицы перехода T = 
 tij
tij 
 , i, j = 1,...,n , являются координатами в
, i, j = 1,...,n , являются координатами в
разложении векторов e1¢ ,e¢2,...,e¢n по базису (I). Справедливость этого замечания непосредственно следует из равенств (11.1). Замечание2. Матрица перехода от базиса к базису является невырожденной матрицей. Теорема. Пусть V - линейное пространство, e1,e2,...,en (I) и
e1,e2 |
,...,en |
(II) - два базиса в V , |
T - матрица перехода от (I) к (II), x Î V , x = a1e1 + a2e2 + ...+ anen и |
||||||||||||||||||||
¢ |
|
¢ |
|
¢ |
|
|
|
+ ...+ bnen , тогда |
|
|
|
|
|
|
|
|
|
|
|
||||
x = b1e1 + b2e2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
¢ |
|
|
¢ |
|
|
¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
æ b1 |
ö |
|
|
æ a1 ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ç |
|
÷ |
|
|
ç |
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
çb2 |
÷ |
= T -1 |
ç a2 ÷ |
(11.2) Доказательство. Подставим в разложение x по базису (II) выражения |
|||||||||||||||||||
ç ... |
÷ |
|
|
ç |
... ÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ç |
|
÷ |
|
|
ç |
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
èbn |
ø |
|
|
è an ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ei¢, |
i = 1,2,...,n |
из (11.1), получим |
|
|
|
|
|
|
|
|
|
||||||||||||
x = b e¢ + b |
e¢ |
+ ...+ b |
e¢ = |
n |
|
= |
n |
|
æ |
n |
t |
|
ö |
|
= |
|
|||||||
b e¢ |
b ç |
|
e |
÷ |
|
|
|||||||||||||||||
|
|
1 1 |
2 |
2 |
|
n |
n |
å |
i i |
|
|
i |
|
|
|
ki k |
|
b |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1вносимå |
ç åпод знак÷ |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
i=1 |
|
è k =1 |
|
|
|
|
i |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø внутренней суммы |
||||||||
= |
n |
æ |
n |
|
|
|
|
ö |
= |
|
n |
æ |
n |
|
|
|
ö |
|
= |
|
|
||
|
|
ç |
b t |
|
e |
÷ |
|
|
ç |
b t |
e |
÷ |
|
|
|
||||||||
|
åç |
å i |
|
ki |
k |
÷ меняем порядок åç å i |
ki k ÷ |
выносим e |
|
||||||||||||||
|
i=1 è k=1 |
|
|
|
|
ø суммирования |
k=1è i=1 |
|
|
|
ø |
за знак |
k |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
внутренней суммы |
||||
|
n |
æ |
n |
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
åbitki |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= åç |
÷ ek . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
k =1 |
è i=1 |
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Последнюю сумму запишем развернуто: |
|
|
|
|
|||||||||||||||||||
n æ |
n |
|
|
ö |
|
æ n |
b t |
ö |
æ n |
b t |
|
ö |
|
|
æ |
n |
|
ö |
|||||
|
ç |
|
b t |
ki |
÷ e |
= ç |
÷ e |
+ ç |
|
|
÷ e |
+ ...+ ç |
b t |
ni |
÷ e = |
||||||||
åç å i |
÷ |
k |
ç å i 1i ÷ 1 |
ç å i |
2i ÷ 2 |
|
|
ç |
å i |
÷ n |
|||||||||||||
k=1è i=1 |
|
|
ø |
|
è i=1 |
ø |
è i=1 |
|
|
ø |
|
|
è i=1 |
|
ø |
||||||||
= (b1t11 + b2t12 + ...+ bnt1n )e1 + (b1t21 + b2t22 + ...+ bnt2n )e2 + ...+ +(b1tn1 + b2tn2 + ...+ bntnn )en .
По условию x = a1e1 + a2e2 + ...+ anen , используя теорему о единственности разложения вектора по базису, получим
a1 = b1t11 + b2t12 + ...+ bnt1n ,
a2 = b1t21 + b2t22 + ...+ bnt2n ,
……………………………………
an = b1tn1 + b2tn2 + ...+ bntnn ,
æ a1 |
ö |
æ b1 |
ö |
æ b1 |
ö |
æ a1 |
ö |
ç |
÷ |
ç |
÷ |
ç |
÷ |
ç |
÷ |
что в матричном виде выглядит как равенство ç a2 |
÷ |
= T çb2 |
÷ |
.Отсюда следуетçb2 |
÷ |
= T -1 ç a2 |
÷ . |
ç ... |
÷ |
ç ... |
÷ |
ç ... |
÷ |
ç ... |
÷ |
ç |
÷ |
ç |
÷ |
ç |
÷ |
ç |
÷ |
è an |
ø |
èbn |
ø |
èbn |
ø |
è an |
ø |
Теорема доказана. |
|
|
|
|
|
|
|
19.Линейные подпространства. Примеры.
Определение. Пусть V - линейное пространство. Непустое подмножество L линейного пространства V ( L Í V,L ¹ Æ ) называется линейным подпространством в V , если выполняются
два условия:
1) "x Î L "y Î L (x + y) Î L ;
Created with ReaSoft PDF Printer free trial.
Purchase at http://www.reasoft.com/
2) "x Î L при любом вещественном числе l (lx) Î L .
Пример. Пусть - линейное пространство всех арифметических n -мерных векторов (x1,...,xn ) ; L - совокупность всех векторов, у которых первая и последняя компоненты равны
нулю, т.е. векторов вида (0,x2 ,...,xn-1,0) . L - подпространство в Rn .Действительно, пусть xÎ L и y Î L , следовательно, по определению L x = (0, x2 ,...,xn-1, 0) и y = (0, y2 ,..., yn-1, 0) . По правилу сложения векторов в Rn x + y = (0, x2 + y2 ,..., xn-1 + yn-1,0)Î L и, таким образом, сумма любых двух
векторов из L принадлежит L . Пусть xÎ L и l - произвольное вещественное число. Но x Î Rn (так как L Í Rn ), следовательно, по правилу умножения вектора на число в Rn
lx = (l ×0, lx2 ,...,lxn-1, l ×0) = (0,lx2,lx3,...,0)Î L и вместе с любым вектором произведение его на l тоже принадлежит L . В соответствии с определением 2 это означает, что L - линейное
подпространство в Rn . Замечание. Если L - линейное подпространство в V , то L само является линейным пространством относительно введенных в V операций сложения и умножения на число. Действительно, требования 1) и 2) в определении означают, что в L определены операции сложения векторов и умножения вектора на число.
Аксиомы 1 и 2 выполняются в L , так как они имеют место в V . Убедимся в справедливости аксиомы 3.Пусть xÎ L , l = 0 , следовательно, согласно условию 2) 0× x Î L , но по следствию 5 из аксиом в V 0× x = q , таким образом, q Î L и в L справедлива аксиома 3.
Пусть xÎ L , l = -1 . Следовательно, согласно условию 2) (-1)× x Î L , но по следствию 8 из аксиом в V (-1)× x = -x , таким образом, (-x) Î L и в L справедлива аксиома 4.
Аналогично проверяется справедливость аксиом 5 - 8, следовательно, L - линейное пространство.
Пусть V - произвольное линейное пространство, a1,a2,...,ak - некоторая система векторов в V . Рассмотрим совокупность всех векторов вида l1a1 + l2a2 + ...+ lk ak , где l1,l2,...,lk принимают
всевозможные вещественные значения. Обозначим множество этих векторов
L = {l1a1 + l2a2 + ...+ lk ak }. L называется линейной оболочкой векторов a1,a2,...,ak . L является
подпространством в V .
Действительно, L Í V,L ¹ Æ (так как, например, сами векторы ai , i = 1,...,k , принадлежат L ). Пусть aÎ L , b Î L , следовательно, по определению L $ l1,l2,...,lk ,m1,m2,...,mk такие, что
a = l1a1 + l2a2 + ...+ lk ak , b = m1a1 + m2a2 + ...+ mk ak .
Имеем a + b = (l1 + m1)a1 + (l2 + m2 )a2 + ...+ (lk + mk )ak и (a + b) Î L .
Пусть aÎ L , d - произвольное вещественное число. Имеем
da = d(l1a1 + l2a2 + ...+ lk ak ) = (dl1 )a1 + ...+ (dlk )ak и (da) Î L .
Таким образом, выполняются условия 1) и 2) определения 2 и L является линейным подпространством в V .
Говорят, что L порождено системой векторов a1,a2,...,ak или L "натянуто" на систему a1,a2,...,ak . Заметим, что само линейное пространство V может рассматриваться как линейная оболочка любого своего базиса.
20.Линейные операторы, определение и примеры.
Определение. Пусть V - линейное пространство и каждому вектору x , принадлежащему V , поставлен в соответствие вектор y , y Î V . Соответствие A : x ® y называется оператором,
определенным в линейном пространстве V .Принята также запись: y = A(x) . Вектор x называется прообразом, а y - образом при отображении оператором A .Определение. Оператор A ,
определенный в линейном пространстве V , называется линейным, если:
1) "x Î V "y Î V A(x + y) = A(x) + A(y) ; 2) "x Î V "l - вещественного числа A(lx) = lA(x) .
Created with ReaSoft PDF Printer free trial.
Purchase at http://www.reasoft.com/
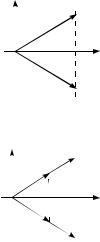
Пример. |
V - линейное пространство всех геометрических векторов плоскости, |
A - зеркальное |
||||||||||||||||||||||||||||||||||||||||||||
отражение относительно оси Ox (рис. 12.1). A - линейный оператор. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
y |
|
Убедимся, что выполняется требование 2) в определении 2.Пусть l - произвольное |
||||||||||||||||||||||||||||||||||||||||||||
x |
|
вещественное число, по определению умножения на l для геометрического вектора |
||||||||||||||||||||||||||||||||||||||||||||
|
x |
x вектор OB = lx имеет то же направление, что и x , если l > 0 , |
и противоположное, |
|||||||||||||||||||||||||||||||||||||||||||
|
|
если |
l < 0 , и |
|
= |
|
l |
|
× |
|
. Рис. 12.2 соответствует случаю l > 0 , |
|
l |
|
> 1 ( l < 0 |
|||||||||||||||||||||||||||||||
A(x) |
|
OB |
|
|
x |
|
|
|||||||||||||||||||||||||||||||||||||||
Рис. 12.1 |
|
рассматривается аналогично). Пусть OK = x , |
OB = lx , OP - зеркальное отражение |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
B |
вектора OK относительно оси Ox , |
OD - зеркальное отражение вектора OB . Тогда |
|||||||||||||||||||||||||||||||||||||||||||
K |
|
OKP ~ OBD и, значит, |
|
OB |
= |
OD |
. Но |
|
= |
|
l |
|
× |
|
, поэтому |
|
= |
|
l |
|
|
× |
|
. Кроме |
||||||||||||||||||||||
|
C |
|
OB |
|
|
OK |
OD |
|
|
|
OP |
|||||||||||||||||||||||||||||||||||
|
|
OK |
OP |
|||||||||||||||||||||||||||||||||||||||||||
O |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P |
|
того, направление вектора OP совпадает с направлением вектора OD , следовательно, |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= A(x) ü |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 12.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
OP |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
Þ A(lx) = lA(x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
OD = l ×OP . Таким образом, имеем OD |
= A(lx)ý |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
OD |
= l ×OPï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
þ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так же, |
исходя из геометрических соображений, можно доказать, что A(x + y) = A(x) + A(y) , |
|||||||||||||||||||||||||||||||||||||||||||||
следовательно, оператор A зеркального отражения относительно оси Ox является линейным |
||||||||||||||||||||||||||||||||||||||||||||||
оператором. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
21.Матрица линейного оператора. Связь координат образа и прообраза. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Определение. Пусть V - линейное пространство, |
e1,e2,...,en - базис в V , A - линейный оператор в |
|||||||||||||||||||||||||||||||||||||||||||||
V . Матрицей линейного оператора A в базисе e1,e2,...,en |
называется матрица Q = |
|
|
|
aij |
|
|
|
, i, j = 1,..,n , |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
такая, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A(e1) = a11e1 + a21e2 + ...+ an1en ,
A(e2 ) = a12e1 + a22e2 + ...+ an2en ,
……………………………………..
A(en ) = a1ne1 + a2ne2 + ...+ annen .
Замечание. Столбцы матрицы Q являются координатами в разложении векторов
A(e1), A(e2 ),..., A(en ) по базису e1,e2,...,en . Замечание 2 . Пусть V - линейное пространство, A - линейный оператор в V , e1,e2,...,en (I) - базис в V . Матрица оператора в базисе (I) определена однозначно. Для того, чтобы в этом убедиться, разложим векторы A(e1),A(e2 ),..., A(en ) по базису
(I). Столбцы матрицы Q представляют собой координаты этих векторов, которые согласно теореме 3 лекции 10 определяются единственным образом, следовательно, матрица Q оператора A в (I) определена однозначно. Теорема. Пусть V - линейное пространство, e1,e2,...,en (I) - базис в V , A - линейный оператор в V , Q = 
 aij
aij 
 , i, j,= 1,...,n - матрица линейного оператора A в базисе
, i, j,= 1,...,n - матрица линейного оператора A в базисе
(I), x Î V , x = x1e1 + ...+ xnen , y = A(x) , y = y1e1 + ...+ ynen . Тогда
æ |
y |
ö |
æ x |
ö |
||
ç |
|
1 |
÷ |
ç |
1 |
÷ |
ç ... |
÷ |
= Q ç ... |
÷ . |
|||
ç y |
n |
÷ |
ç x |
÷ |
||
è |
|
ø |
è |
n |
ø |
|
Доказательство. Имеем
y = A(x) = A(x e + ...+ x e |
|
) |
|
= |
x A(e ) + ...+ x A(e |
|
) = |
|
|
|
|||||||||||
|
|
|
1 1 |
|
|
n |
n |
|
А - линейный |
1 |
1 |
|
n |
|
n |
|
|
|
|
||
= |
n |
) = |
|
n |
æ |
n |
|
|
|
ö |
= |
|
|
n æ |
n |
|
|
|
|
|
|
x A(e |
|
x |
ç |
|
|
a e |
÷ |
|
|
ç |
|
|
x a e |
|
|||||||
|
å i i |
(12.1) |
å i ç |
å ki |
k ÷ вносим |
xпод |
|
åç |
å i |
ki |
|
k |
|||||||||
|
i=1 |
|
|
i=1 |
è k =1 |
|
|
|
|
i |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
ø знак внутренней суммы i=1 è k =1 |
|
|
|
|
||||||||||||
|
= |
|
n |
æ |
n |
|
|
|
|
ö |
= |
|
n |
æ |
n |
|
|
ö |
|
. |
|
|
|
|
ç |
|
x a e |
|
÷ |
|
|
ç |
x a |
|
÷e |
|
|
||||||
меняем порядок |
åç |
å i |
ki |
|
k |
÷ |
выносим еk за |
åç |
å i ki ÷ |
k |
|
|
|||||||||
суммирования |
k =1 |
è i=1 |
|
|
|
|
ø знак внутренней суммы k =1 |
è i=1 |
|
|
ø |
|
|
|
|||||||
Created with ReaSoft PDF Printer free trial.
Purchase at http://www.reasoft.com/
ö
÷ =
÷
ø
n
По условию y = y1e1 + ...+ ynen = å yk ek .
k =1
Используя теорему о единственности разложения вектора по базису, получим
n
"k, k = 1...n, yk = åxiaki =x1ak1 + x2ak 2 + ...+ xnakn
i=1
Заметим, что в последнем равенстве числа ak1,ak 2,...,akn - элементы k-й строки матрицы Q . Привлекая правило умножения матриц, равенство запишем в виде
æ |
y |
ö |
æ x |
ö |
||
ç |
|
1 |
÷ |
ç |
1 |
÷ |
ç ... |
÷ |
= Q ç ... |
÷ . |
|||
ç y |
n |
÷ |
ç x |
÷ |
||
è |
|
ø |
è |
n |
ø |
|
Теорема доказана.
22.Характеристический многочлен и характеристические корни матрицы.
Определение. Квадратные матрицы B и C называются подобными, если существует невырожденная матрица Q , такая, что C = Q-1BQ . Теорема. Пусть V - линейное пространство,
e1,e2,...,en (I) и e1 |
,e2 |
,...,en (II) - два базиса в V , |
T - матрица перехода от (I) к (II), A - линейный |
|||||||||
|
|
|
|
|
|
|
|
|
¢ |
¢ |
¢ |
|
оператор в V , |
B - матрица оператора A в (I), |
C - матрица оператора A в (II). Тогда |
||||||||||
C = T -1BT . |
|
|
|
|
||||||||
Пусть A = |
|
|
|
aij |
|
|
|
, |
i, j,= 1...n . Матрица A - lE , где E - единичная матрица порядка n , а l - |
|||
|
|
|
|
|||||||||
произвольное вещественное число, называется характеристической матрицей для A . Она имеет вид
æ a11 - l |
|
a12 |
... |
a1n |
ö |
||||||||
ç |
a |
|
a |
|
|
- l |
... |
a |
÷ |
||||
A - lE = ç |
21 |
22 |
|
|
|
... |
2n |
÷ . |
|||||
ç .... |
|
|
... |
|
|
... |
÷ |
||||||
ç |
an1 |
|
an2 |
|
|
÷ |
|||||||
è |
|
... |
ann - l ø |
||||||||||
Определитель |
|
A - lE |
|
|
- некоторый многочлен порядка n относительно l . Определение. |
||||||||
|
|
||||||||||||
Многочлен |
|
A - lE |
|
|
называется характеристическим многочленом матрицы A , а его корни - |
||||||||
|
|
|
|||||||||||
характеристическими корнями матрицы A .Теорема. Подобные матрицы имеют одинаковый набор характеристических корней. Доказательство. Пусть C = Q-1BQ , Q - невырожденная матрица. Имеем C - lE = Q-1BQ - lE = Q-1BQ - Q-1(lE)Q =
= |
|
Q-1(B - lE)Q |
|
= |
|
Q-1 |
|
× |
|
B - lE |
|
× |
|
Q |
|
= |
|
B - lE |
|
. |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
свойства |
|
|
|
теорема об |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
умножения |
|
|
|
определителе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
матриц |
|
|
|
произведения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
матриц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Характеристические многочлены матриц В и С совпадают, следовательно, совпадают и характеристические корни. Теорема доказана. Следствие. Матрицы, задающие линейный оператор в различных базисах, имеют один набор характеристических корней
23.Характеристические корни и собственные значения линейного оператора.
Определение. Характеристические корни матрицы линейного оператора (в любом базисе) называются характеристическими корнями линейного оператора. Определение. Весь набор характеристических корней называется спектром оператора. Определение. Пусть V - линейное пространство, A - линейный оператор в V . Вектор x ¹ q называется собственным вектором оператора A , если найдется действительное число l такое, что A(x) = lx . Число l называется
собственным значением, соответствующим данному собственному вектору x . Теорема. Действительные характеристические корни линейного оператора, если они существуют, и только они, служат собственными значениями линейного оператора. Пример. Найти
Created with ReaSoft PDF Printer free trial.
Purchase at http://www.reasoft.com/
собственные векторы и собственные значения линейного оператора зеркального отражения
|
|
|
|
|
|
|
|
|
æ |
1 |
0 |
ö |
|
|
|
|
|
|
|
|
|
|
относительно оси Ox . Решение. Q = ç |
|
|
÷ . Составим характеристическое уравнение: |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
è |
0 |
-1ø |
|
|
|
|
|
|
|
|
|
|
|
|
Q - lE |
|
= |
|
1- l |
0 |
|
= 0 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
0 -1- l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
откуда (1- l)(-1- l) = 0 |
и l1 = 1 , l2 = -1. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Числа l1 = 1 , l2 = -1 - характеристические корни линейного оператора, они действительны и, |
||||||||||||||||||||||
согласно теореме, являются собственными значениями. Найдем соответствующие им |
|
|
|
|
||||||||||||||||||
собственные векторы. По определению собственного вектора x A(x) = lx , но A(x) = Qx , |
|
|
|
|||||||||||||||||||
следовательно, ищем векторы, удовлетворяющие уравнению Qx = lx , или Qx = lEx , или |
|
|
|
|||||||||||||||||||
(Q - lE)x = q (12.3) При l = 1 имеем Q - l E = æ |
0 |
0 |
ö |
. Подставим ее в (12.3): æ |
0 0 |
öæ x1 |
ö = |
æ |
0 |
ö , |
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
1 |
ç |
0 -2 |
÷ |
ç |
0 -2 |
֍ x |
÷ |
ç |
0 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
ø |
è |
|
øè 2 |
ø |
è |
|
ø |
|
|
|
|
|
|
|
|
|
ì0× x1 + 0× x2 = 0, |
(12.4) откуда x2 = 0 , и решением системы |
||||||||||||
что равносильно системе уравнений í0× x - 2× x |
= 0, |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
î |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
(12.4) являются все векторы вида X (1) = |
æ c1 |
ö , c - произвольное вещественное число, отличное от |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ç |
÷ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è 0 |
ø |
|
|
|
|
|
|
|
|
|
|
нуля. При l2 = -1 получаем |
æ 2 |
0ö |
, подставляем в (12.3): |
æ 2 |
0öæ x |
ö |
æ |
0ö |
, получаем |
|||||
Q - l2E = ç |
|
|
÷ |
ç |
|
|
֍ 1 |
÷ |
= ç |
|
÷ |
|||
|
è |
0 |
0 |
ø |
|
è |
0 |
0 |
øè x2 ø |
è |
0 |
ø |
|
|
систему уравнений |
ì2× x1 |
+ 0× x2 |
= 0, |
откуда |
X (2) = |
æ |
0 |
ö |
, с - произвольное вещественное число, |
|
|
í0× x + 0× x = 0, |
|
|
ç |
с |
÷ |
2 |
|||
|
î |
1 |
2 |
|
|
|
è |
2 |
ø |
|
отличное от нуля. |
|
|
y |
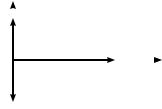
Геометрически это означает, что любой ненулевой вектор, приложенный к |
|
A(y) |
началу координат с концом на оси Ox , является собственным, отвечающим |
|
x=A (x) - собств., l=1 |
собственному значению l1 = 1 (действие на него оператора A сводится к |
|
x |
умножению его на l = 1 , а любой ненулевой вектор с концом на оси Oy |
|
y - собств., l= -1 |
1 |
|
является собственным, отвечающим собственному значению l2 = -1 (т.е. |
||
Рис. 12.5 |
действие оператора A на этот вектор заключается в умножении его на l2 = -1 (рис. 12.5)).
24.Линейная независимость собственных векторов, относящихся к различным собственным значениям.
Теорема. Пусть V - линейное пространство, A - линейный оператор в V , b1,b2,...,bk - собственные векторы оператора A , отвечающие собственным значениям l1,l2,...,lk . Если
"i "j, i ¹ j Þ li ¹ l j , то b1,b2,...,bk
- линейно независимы. Доказательство. Доказательство
проведем индукцией по числу векторов k . При k = 1 имеем один вектор bθ¹ (по определению
1
собственный вектор отличен от нулевого), вектор b1 составляет линейно независимую систему.
Пусть утверждение теоремы справедливо для k -1: всякая система k -1 собственных векторов, отвечающих различным собственным значениям, является линейно независимой. Пусть имеется система k собственных векторов b1,b2,...,bk , относящихся к различным собственным значениям
l1,l2,...,lk ( "i "j, i ¹ j Þ li ¹ l j ). Предположим, система b1,b2,...,bk линейно зависима, т.е. найдутся числа a1,a2,...,ak , не все равные нулю, такие, что выполняется равенство
a1b1 + a2b2 + ...+ ak bk = q .(12.7) Не ограничивая общности рассуждений, можем считать, что a1 ¹ 0 (иначе перенумеруем векторы). Применим к обеим частям равенства (12.7) оператор A :
A(a b + a |
|
b |
|
+ ...+ a |
|
b |
|
) |
= |
a A(b ) + ...+ a |
|
A(b |
|
) = |
1 1 |
2 |
|
2 |
|
k |
|
k |
|
A - линейный |
1 1 |
k |
|
k |
|
= a1l1b1 + ...+ ak lk bk = A(q) = q .
bi - cобственные, i=1,...,n
Из последнего равенства получим a1l1b1 + ...+ ak lk bk = q .(12.8)
Created with ReaSoft PDF Printer free trial.
Purchase at http://www.reasoft.com/
Обе части равенства (12.7), умноженные на lk , вычтем почленно из обеих частей (12.8), получим
a1(l1 - lk )b1 + ...+ ak-1(lk-1 - lk )bk-1 = q . Равенство означает, что векторы b1,b2,...,bk-1 линейно зависимы (их линейная комбинация с коэффициентами, не равными одновременно нулю, например, коэффициент при b1 отличен от нуля, равна θ ), но это противоречит предположению
индукции: векторы b1,b2,...,bk-1 собственные, относящиеся к различным собственным значениям. Следовательно, b1,b2,...,bk - линейно независимы, и утверждение теоремы справедливо при любом k . Теорема доказана.
25.Линейные операторы с простым спектром.
Линейный оператор A задается в базисе e1,e2,...,en (I) диагональной матрицей тогда и только
тогда, когда все векторы базиса (I) - собственные. Определение. Линейный оператор A называется линейным оператором с простым спектром, если все его характеристические корни действительны и различны. Теорема. Всякий линейный оператор с простым спектром может быть задан диагональной матрицей. Доказательство. Пусть V - линейное пространство,
dim V = n , A - линейный оператор в V , A имеет простой спектр. Тогда характеристических корней n . Пусть это числа l1,l2,...,ln , в силу теоремы 4 l1,l2,...,ln - собственные значения оператора A . Пусть e1,e2,...,en - соответствующие этим собственным значениям собственные векторы, тогда согласно теореме 5 e1,e2,...,en линейно независимы, и так как dim V = n , e1,e2,...,en - базис. В этом базисе, как было отмечено выше, матрица оператора имеет вид
æ l1 |
0 ... |
|
ç |
0 |
l2 ... |
Q = ç |
|
|
ç ... ... ... |
||
ç |
0 |
0 ... |
è |
||
0 ö
0 ÷÷ и является диагональной матрицей. Теорема доказана.
... ÷÷ ln ø
26.Евклидовы пространства. Определение и примеры. Следствия из аксиом.
Определение. Евклидовым пространством En называется n-мерное линейное пространство, в котором каждой паре векторов x,y поставлено в соответствие вещественное число, называемое скалярным произведением векторов x и y (это число обозначим (x,y) ), причем выполняются
следующие аксиомы: 1."x Î En "y Î En (x,y) = (y,x) ; 2."x Î En "y Î En "z Î En (x + y,z) = (x,z) + (y,z) ; 3."x Î En "y Î En "l Î R (lx,y) = l(x,y) ; 4."x Î En x ¹ q Þ (x,x) > 0 .Замечание. Аксиомы 2 и 3
справедливы также в форме 2’: (x,y + z) = (x,y) + (x,z) и форме 3’: (x,ly) = l(x,y) . Пример. Пусть
V3 - линейное пространство геометрических векторов, скалярное произведение определено равенством
(x,y) = |
|
x |
|
× |
|
y |
æ |
Ù ö |
. Аксиомы 1 - 4 выполняются, следовательно, со скалярным произведением, |
|||||||||
|
|
|
×cosç x,y ÷ |
|||||||||||||||
|
|
|
|
|
|
|
è |
ø |
|
|
|
|
|
|
|
|
|
|
определенным равенством, V3 является евклидовым пространством. Пример. В линейном |
||||||||||||||||||
пространстве арифметических векторов Rn формула (x,y) = x |
y |
+ x |
y |
2 |
+ ...+ x |
y |
n |
, где x = (x ,x |
,...,x ) , |
|||||||||
|
|
|
|
|
|
|
|
|
1 |
1 |
2 |
|
n |
|
1 2 |
n |
||
y = (y1, y2 ,..., yn ) , задает скалярное произведение. Докажем это. Проверим выполнение аксиом 1 - 4. Поскольку компоненты xi , yi i = 1,...,n - вещественные числа, имеем
(x,y) = x1y1 + ...+ xn yn = y1x1 + ...+ yn xn = (y,x), следовательно, аксиома I выполняется. Пусть
z = (z , z |
2 |
,..., z |
n |
) Î Rn . По определению сложения в Rn x + y = (x |
+ y ,..., x |
+ y |
n |
) . Имеем |
|||||||||
1 |
|
|
|
|
|
|
|
|
|
1 |
1 |
n |
|
|
|||
(x + y,z) |
|
= |
(x |
|
+ y )z |
+ ...+ (x |
+ y |
|
)z |
|
= |
|
|
|
|
|
|
|
(13.2) |
|
1 |
1 1 |
n |
|
n |
|
n |
|
|
|
|
|
|
||
=(x1z1 + y1z1) + ...+ (xn zn + yn zn ) =
=(x1z1 + ...+ xn zn ) + (y1z1 + ...+ yn zn ) = (x,z) + (y,z) ,
аксиома 2 справедлива. Пусть l - произвольное вещественное число. По определению
умножения вектора на число в Rn lx = (lx |
,lx |
,...,lx ) . Далее имеем |
1 |
2 |
n |
Created with ReaSoft PDF Printer free trial.
Purchase at http://www.reasoft.com/

(lx,y) = (lx1)y1 + ...+ (lxn )yn = l(x1y1 + ...xn yn ) = l(x,y) , аксиома 3 выполняется. Проверим выполнение |
|||||
(13.2) |
|
|
|
|
|
аксиомы 4: (x,x) = x2 |
+ ...+ x2 |
. Если x ¹ q , то среди компонент вектора |
x |
найдется x ¹ 0 , 1 £ i £ n , |
|
(13.2) |
1 |
n |
|
|
i |
|
|
|
|
|
|
тогда x12 + ...+ xn2 > 0 и (x,x) > 0 , следовательно, аксиома 4 выполняется. Таким образом, линейное
пространство арифметических векторов Rn со скалярным произведением является евклидовым пространством.
В любом евклидовом пространстве En справедливы следствия из аксиом 1 - 4:
k l
а) "x Î En (x,q) = 0 ; б) если x = a1a1 + ...+ ak ak , y = b1b1 + ...+ blbl , то (x,y) = ååaib j (ai ,bj).
i=1 j=1
27.Норма вектора. Неравенство Коши-Буняковского.
Определение. Нормой вектора x Î En называется число, равное (x,x) . Обозначим норму 
 x
x
 . Норма
. Норма 
 x
x
 - аналог длины вектора, определенной для геометрических векторов. Угол между векторами x и y в евклидовом пространстве определяется равенством
- аналог длины вектора, определенной для геометрических векторов. Угол между векторами x и y в евклидовом пространстве определяется равенством
æ |
Ù |
ö |
|
|
|
(x,y) |
æ |
Ù |
|||||
cosç x,y ÷ |
= |
|
|
Покажем, что угол ç x,y |
|||||||||
|
|
x |
|
× |
|
y |
|
||||||
è |
|
ø |
|
|
|
|
|
|
è |
|
|||
ö
÷ действительно можно определить равенством, т.е.
ø
покажем, что |
|
|
|
(x,y) |
|
£ 1 . Теорема. (неравенство Коши - Буняковского). Для любого x Î En и |
||||||
|
|
|||||||||||
|
|
x |
|
× |
|
y |
|
|||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
любого y Î En справедливо неравенство (x,y)2 £ 
 x
x
 2 ×
2 × 
 y
y
 2 . Доказательство. Пусть a - произвольное вещественное число. Положим a = x - ay . Тогда по аксиоме 4 имеем (a,a) = (x - ay,x - ay) ³ 0 . Воспользуемся аксиомами 1 - 3:
2 . Доказательство. Пусть a - произвольное вещественное число. Положим a = x - ay . Тогда по аксиоме 4 имеем (a,a) = (x - ay,x - ay) ³ 0 . Воспользуемся аксиомами 1 - 3:
f (a) = (x - ay,x - ay) = (x,x) - 2a(x,y) + a2 (y,y) ³ 0 .Так как "a f (a) ³ 0 , то дискриминант D квадратного трехчлена f (a) неположителен: D = 4(x,y)2 - 4(x,x)(y,y) £ 0 . Отсюда (x,y)2 £ (x,x)(y,y) или
(x,y)2 £ 
 x
x
 2 ×
2 × 
 y
y
 2 , и неравенство выполняется. Теорема доказана.
2 , и неравенство выполняется. Теорема доказана.
28.Линейная независимость системы ненулевых ортогональных векторов в евклидовом пространстве.
Определение. Пусть En - евклидово пространство, x Î En , y Î En . Векторы x и y называются ортогональными, если (x,y) = 0 . Определение. Система векторов a1,a2,...,ak называется ортогональной системой векторов в евклидовом пространстве En , если (ai ,a j ) = 0 при
i ¹ j, i, j = 1,..,k . Теорема. В евклидовом пространстве En всякая система ненулевых ортогональных векторов линейно независима. Доказательство. Пусть a1,a2,...,ak - произвольная ортогональная система векторов в En ; "i = 1,..,k ai ¹ q . Пусть a1a1 + ...+ ak ak = q .Умножим обе
части скалярно на a1: a1(a1,a1) + a2 (a2 ,a1) + ...+ ak (ak ,a1) = (q,a1) .Поскольку система векторов
a1,a2,...,ak ортогональна, то верны равенства (a2 ,a1) = 0 ,…, (ak ,a1) = 0 ; следствие а) из аксиом дает (q,a1) = 0 ; согласно аксиоме 4 (a1,a1) > 0 . Тогда из равенства получим a1 = 0 . Аналогично, скалярно умножая a1a1 + ...+ ak ak = q последовательно на a2,...,ak , получим a2 = ... = ak = 0 , следовательно, система a1,a2,...,ak линейно независима. Теорема доказана.
29.Процесс ортогонализации Шмидта.
Опишем процесс построения ортогонального базиса в линейной оболочке любых k линейно независимых векторов. Пусть a1,a2,...,ak линейно независимы. Шаг 1. Примем b1 = a1 .Шаг 2.
Примем b2 = a1b1 + a2 . Отметим, что b2 ¹ q , так как b2 является линейной комбинацией a1 и a2 , причем a1 и a2 линейно независимы (линейная комбинация векторов a1 и a2 с коэффициентами,
Created with ReaSoft PDF Printer free trial.
Purchase at http://www.reasoft.com/
один из которых, а именно коэффициент при a2 , заведомо отличен от нуля, не может равняться
q ).Подберем a |
так, чтобы (b ,b |
|
) = 0 : (a b + a |
|
,b ) = a (b ,b ) + (a |
|
,b ) = 0 и a |
= |
|
|
- |
(a2,b1) |
|
.Шаг |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
(b ,b ) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
1 1 |
|
|
|
2 |
1 |
|
|
|
1 1 |
1 |
|
2 |
1 |
1 |
b ¹qÞ |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(b1,b1)¹0 |
|
|
|
|
|
|
|
|
|
|||
3. Примем b3 = b1b1 + b2b2 + a3 . Отметим, что b3 ¹ q , так как b3 |
является линейной комбинацией |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a1, a2 |
и a3 , а эти векторы линейно независимы. Подберем b1 |
и b2 так, чтобы (b3,b1) = 0 |
и |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(b3,b2 ) = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ì (b |
|
,b ) = (b b + b |
|
b |
|
+ a |
|
|
,b ) = b (b ,b )+ b |
|
|
(b |
|
,b )+ (a |
|
|
,b ) = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
ï |
|
|
3 |
|
1 |
1 |
1 |
2 |
|
|
2 |
|
|
3 |
|
1 |
1 |
1¹0 |
1 |
|
2 |
|
2=0 |
1 |
|
|
3 |
|
1 |
|
Отсюда b |
= - |
(a3,b1) |
, |
b |
|
= - |
(a3,b2 ) |
.Шаг |
|||||||||||||||||||||||
í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
(b |
|
,b |
|
) = (b b + b |
b |
|
|
+ a |
|
|
,b |
|
) = b (b ,b |
|
)+ b |
|
(b |
|
,b |
|
)+ (a |
|
|
,b |
|
) = 0. |
|
|
|
1 |
|
(b ,b ) |
|
|
|
(b |
|
,b |
|
) |
|
|||||||||||||||||||||
ï |
3 |
2 |
2 |
3 |
2 |
2 |
2 |
2 |
2 |
3 |
2 |
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
1 |
2 |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=0 |
|
|
|
|
|
|
|
¹0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4. Пусть уже построена ортогональная система ненулевых векторов b1,...,bs , причем "i, 1 £ i £ s , bi является линейной комбинацией векторов a1,...,ai . Положим bs+1 = g1b1 + ...+ gsbs + as+1 .Вектор bs+1 ¹ q , так как является линейной комбинацией линейно независимых векторов a1,a2,...,as+1 с коэффициентами, один из которых, а именно коэффициент при as+1 , заведомо отличен от нуля
(поскольку as+1 |
не входит в b1,...,bs ).Коэффициенты g1,..., gs |
подберем так, чтобы bs+1 был |
||
ортогонален векторам |
|
|
|
|
b1,...,bs : (bs+1,bi ) = 0, i = 1,2,..., s .Отсюда(bs+1,bi ) = (g1b1 + ...+ gsbs |
+ as+1,bi ) = g1 (b1,bi )+ ...+ |
|||
|
|
|
|
=0 |
+gi (bi ,bi )+ ...+ gs (bs ,bi )+ (as+1,bi ) = 0 и gi = - |
(as+1,bi ) |
, i = 1,..., s .Продолжая процесс, построим |
||
|
||||
¹0 |
=0 |
(bi ,bi ) |
|
|
ортогональную систему векторов b1,...,bk , причем "i, i = 1,...,k , bi ¹ q , откуда в силу теоремы (В евклидовом пространстве En всякая система ненулевых ортогональных векторов линейно независима) следует, что b1,...,bk линейно независимы. Линейная оболочка L векторов a1,...,ak является подпространством размерности k ( dimL = k ), а это означает, что b1,...,bk - базис в L (по построению - ортогональный).
30.Ортогональные и ортонормированные базисы векторов в евклидовом пространстве
Определение. Вектор a, a Î En называется нормированным, если |
|
|
|
a |
|
|
|
= 1. Если a ¹ q , то |
||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
нормированием называется переход к вектору b = |
|
a |
(b является нормированным, так как |
|||||||||||||||||||||||||||||||
|
a |
|
|
|||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
æ |
|
|
a |
|
|
|
a |
ö |
|
= |
|
|
1 |
|
×(a,a) = 1 |
и, следовательно, |
|
|
|
= 1 ). Определение. Система векторов |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
(b,b) = ç |
|
|
|
|
, |
|
|
|
|
÷ |
= |
|
|
|
|
|
|
b |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
ç |
|
|
a |
|
|
|
|
a |
|
÷ |
|
|
|
|
a |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e1,e2,...,ek в евклидовом пространстве En называется ортонормированной системой, если
ì1, |
если |
i = j |
, |
(ei ,e j ) = í |
если |
i ¹ j, |
i, j = 1,...k. |
î0, |
Всякое евклидово пространство обладает ортонормированными базисами. Возьмем в En произвольный ортогональный базис и нормируем все его векторы, т.е. перейдем к системе векторов
e1 = |
|
|
b1 |
,...,en = |
|
|
bn |
. - ортонормированный базис в En .Теорема. Пусть En - евклидово |
||
|
|
b1 |
|
|
|
bn |
|
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
пространство, e1,...,en (I) – базис в En . Базис e1,...,en является ортонормированным тогда и только
тогда, когда для любых векторов x Î En , y Î En , x = x1e1 + ...+ xnen , y = y1e1 + ...+ ynen скалярное произведение выражается равенством (x,y) = x1y1 + ...+ xn yn . Доказательство. Необходимость.
ì |
i = j, |
1, |
|
Пусть базис (I) – ортонормированный, т.е. (ei ,e j ) = í |
i ¹ j. |
î0, |
Created with ReaSoft PDF Printer free trial.
Purchase at http://www.reasoft.com/
