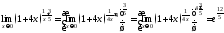- •Образец заполнения титульного листа домашней контрольной работы
- •Методические рекомендации по изучению курса
- •Общие методические указания по выполнению контрольной работы
- •Содержание тем контрольных работ
- •Требования к выполнению и оформлению контрольной работы
- •Вопросы для контроля теоретических знаний
- •1.2. Разложение определителя по элементам строки или столбца
- •1.3. Решение систем линейных уравнений методом определителей (метод Крамера)
- •II. Аналитическая геометрия
- •2.1. Координаты вектора в пространстве. Действия над векторами в координатной форме
- •2.2. Скалярное произведение векторов. Угол между векторами
- •2.3. Векторное произведение векторов
- •2.4. Общее уравнение плоскости
- •2.5. Общее уравнение прямой в пространстве
- •III. Введение в теорию пределов функций
- •Техника вычисления пределов
- •IV. Дифференциальное исчисление
- •4.1. Производная функции
- •4.2. Производные высших порядков функции
- •V. Интегральное исчисление
- •5.3.2. Метод замены переменной
- •5.4. Определенный интеграл и его свойства
- •5.5. Методы вычисления определенного интеграла
- •Задания для контрольной работы
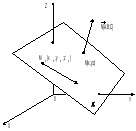
2.3. Векторное произведение векторов
Определение:
векторным
произведением двух векторов
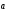 и
и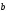 называется
вектор
называется
вектор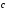 ,
для которого выполняются следующие
условия:
,
для которого выполняются следующие
условия:

Направление
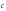 определяется правилом правого буравчика.
определяется правилом правого буравчика.
Обозначение:
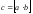 .
.
Свойства:
Допустим:
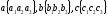 .
.
Тогда:
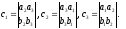
Доказательство:
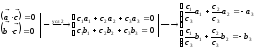
Решаем систему по методу Крамера:
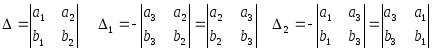
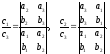
Таким образом:
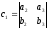 ,
,
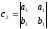 и
и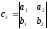 .
.
Следствия:
1.
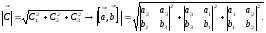
2.
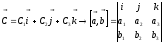 .
.
3.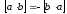 (следствие 2).
(следствие 2).
4.
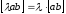 (следствие 2).
(следствие 2).
5.
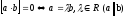 .
.
6.
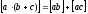 (следствие 2).
(следствие 2).
7.
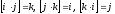 .
.
8.
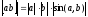 .
.
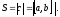
2.4. Общее уравнение плоскости
 нормальный
вектор к плоскости;
нормальный
вектор к плоскости;
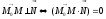 ;
;
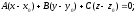
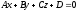 –уравнение
плоскости общего вида.
–уравнение
плоскости общего вида.
Допустим:
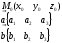


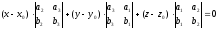
или
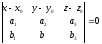 –
задание плоскости через определитель
третьего порядка.
–
задание плоскости через определитель
третьего порядка.
Особые случаи:
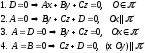
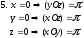
2.5. Общее уравнение прямой в пространстве
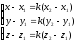
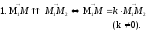
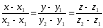 –уравнение
прямой l,
проходящей через данные точки М1(x1,
y1,
z1)
и М2(x2,
y2,
z2).
–уравнение
прямой l,
проходящей через данные точки М1(x1,
y1,
z1)
и М2(x2,
y2,
z2).
2.
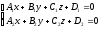 –уравнение
прямой, заданной двумя пересекающимися
плоскостями:
–уравнение
прямой, заданной двумя пересекающимися
плоскостями: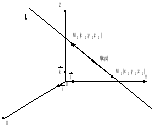
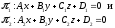
Пример 1.
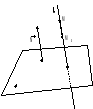
Написать уравнение плоскости, проходящей через точки М1(–1;–2;0) и М2(1;1;2) и перпендикулярной к плоскости : x + 2y + 2z – 4 = 0.
Решение.
Пусть M(x, y, z) – произвольная точка искомой плоскости.
|
|
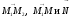 лежат
в одной плоскости, где
лежат
в одной плоскости, где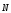 –
нормальный вектор к плоскости.
–
нормальный вектор к плоскости.

Составим
уравнение плоскости, содержащей векторы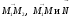 :
:

Раскроем определитель третьего порядка:
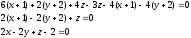
Ответ:
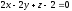 – уравнение плоскости.
– уравнение плоскости.
Пример 2.
Написать уравнение прямой l, перпендикулярной плоскости :
 ,
проходящей через точку
,
проходящей через точку
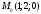 .
.
|
|
1.
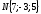 – нормальный вектор к плоскости.
– нормальный вектор к плоскости.
2.
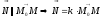 ,
где точкаМ(x,
y,
z)
лежит на искомой прямой l.
,
где точкаМ(x,
y,
z)
лежит на искомой прямой l.
Тогда

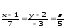 – уравнение
прямой l.
– уравнение
прямой l.
Ответ: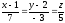 .
.
III. Введение в теорию пределов функций
Определение:
число А
называется пределом функции y
= f(x)
при
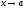 ,
если для любого числа
,
если для любого числа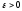 ,
существует
,
существует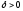 такое,
что при
такое,
что при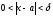 выполняется
неравенство
выполняется
неравенство .
.
Обозначение:
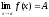 .
.
Основные свойства пределов:
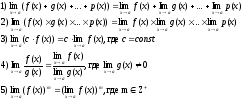
Функция
f(x)
называется непрерывной
в
данной точке a,
если выполняется равенство:
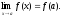
Замечательные пределы:
1.
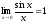 –
первый замечательный предел.
–
первый замечательный предел.
2.
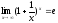 –
второй замечательный предел.
–
второй замечательный предел.
Техника вычисления пределов
Пример 1.
Найти
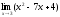 .
.
Решение.
Функция
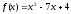 –
непрерывная, графиком ее является
парабола. Следовательно, заменяя ее
аргумент предельным значением, найдем
значение предела:
–
непрерывная, графиком ее является
парабола. Следовательно, заменяя ее
аргумент предельным значением, найдем
значение предела:
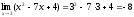 .
.
Ответ: –8.
Пример 2.
Найти
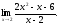
При
непосредственном нахождении предела
и числитель и знаменатель обращаются
в нуль, таким образом, получается
неопределенность вида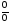 .
.
Чтобы
раскрыть неопределенность
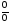 ,
разложим числитель на множители:
,
разложим числитель на множители:
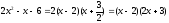 ,
,
и
сократим дробь на выражение (х
– 2), предел которого при
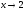 равен
0.
равен
0.
Тогда
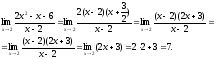
Ответ: 7.
Пример 3.
Найти
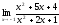 .
.
Решение:
Непосредственно
подстановкой убеждаемся, что выражение
обращается в неопределенность вида
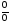 .
.
Разложим числитель и знаменатель на множители:

и сократим дробь на выражение (х + 1). Таким образом
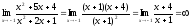 .
.
Ответ: .
Пример 4.
Найти:
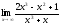 .
.
Решение:
При
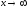 непосредственно подстановкой имеем
неопределенность вида
непосредственно подстановкой имеем
неопределенность вида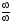 .
.
Чтобы
раскрыть неопределенность, разделим
числитель и знаменатель дроби на
наивысшую степень переменной –
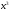 .
Тогда
.
Тогда
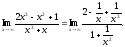
Поскольку
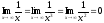 ,
то
,
то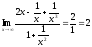 .
.
Ответ: 2.
Пример 5.
Найти:
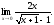
Решение.
Непосредственно
подстановкой имеем неопределенность
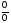 .
Раскроем неопределенность, умножив
числитель и знаменатель на число,
сопряженное к знаменателю дроби:
.
Раскроем неопределенность, умножив
числитель и знаменатель на число,
сопряженное к знаменателю дроби: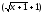
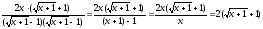 .
Тогда
.
Тогда
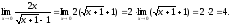
Ответ: 4.
Пример 6.
Найти:
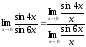 .
.
Решение:
Найдем
пределы, используя первый замечательный
предел
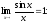
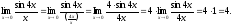
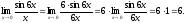
Таким
образом:
 .
.
Замечание:
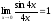 ,
так как если
,
так как если
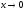 ,
то
,
то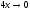 .
.
Значит
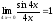 .
.
Ответ:
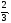
Пример 7.
Найти:
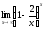 .
.
Решение:
Преобразуем
выражение, стоящее под знаком предела,
к виду
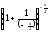 ,
и используем второй замечательный
предел
,
и используем второй замечательный
предел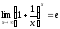 .
.
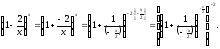
Если
 ,
то
,
то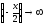 .
Значит:
.
Значит:


Ответ:
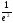 .
.
Рассмотрим теперь методику раскрытия неопределенностей вида 1в точке, как всегда на конкретных примерах.
ПРИМЕР 8.
Вычислить
предел: 9. Р =
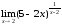 =
(выделим в скобках единицу) =
=
(выделим в скобках единицу) =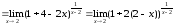 = (в показателе выделим выражение обратное
выражению 2(2 – х), получим)
= (в показателе выделим выражение обратное
выражению 2(2 – х), получим)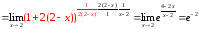 .
.
Аналогично, но без комментариев.
ПРИМЕР 9
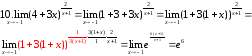
Теперь попроще и потому покороче
ПРИМЕР 10.
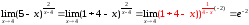
ПРИМЕР 11
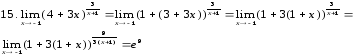
ПРИМЕР 12
а)
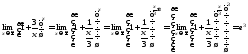 [неопределенность
[неопределенность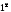
б)
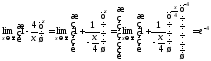 [неопределенность
[неопределенность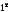 ]
]
в)
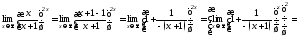

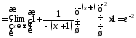 [неопределенность
[неопределенность
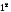 ]
]
ПРИМЕР 13
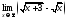 а вот здесь получаем неопределенность
а вот здесь получаем неопределенность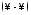 ;
перейдем к неопределенности
;
перейдем к неопределенности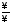 ,
для этого
,
для этого
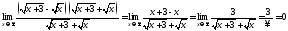
ПРИМЕР 14
 имеем
имеем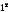 ,
но вторая форма записи второго
замечательного предела
,
но вторая форма записи второго
замечательного предела