- •Образец заполнения титульного листа домашней контрольной работы
- •Методические рекомендации по изучению курса
- •Общие методические указания по выполнению контрольной работы
- •Содержание тем контрольных работ
- •Требования к выполнению и оформлению контрольной работы
- •Вопросы для контроля теоретических знаний
- •1.2. Разложение определителя по элементам строки или столбца
- •1.3. Решение систем линейных уравнений методом определителей (метод Крамера)
- •II. Аналитическая геометрия
- •2.1. Координаты вектора в пространстве. Действия над векторами в координатной форме
- •2.2. Скалярное произведение векторов. Угол между векторами
- •2.3. Векторное произведение векторов
- •2.4. Общее уравнение плоскости
- •2.5. Общее уравнение прямой в пространстве
- •III. Введение в теорию пределов функций
- •Техника вычисления пределов
- •IV. Дифференциальное исчисление
- •4.1. Производная функции
- •4.2. Производные высших порядков функции
- •V. Интегральное исчисление
- •5.3.2. Метод замены переменной
- •5.4. Определенный интеграл и его свойства
- •5.5. Методы вычисления определенного интеграла
- •Задания для контрольной работы
1.2. Разложение определителя по элементам строки или столбца
|
, |
aij – общий элемент определителя, где i – номер строки, j – номер столбца. |
Минором элемента aij определителя D называется определитель второго порядка, полученный из данного вычеркиваниемстроки и столбца, содержащих взятый элемент.
Обозначение: Mij.
Пример.
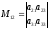 –минор
элемента а12.
–минор
элемента а12.
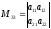 –минор
элемента а33.
–минор
элемента а33.
Алгебраическим дополнением элемента аij называется минор этого элемента, умноженный на коэффициент (–1)i+j.
Обозначение: Аij = (–1)i+j Mij.
Пример.
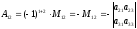 .
.
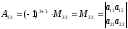 .
.
Теорема:
Если
 ,
то
,
то
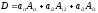 ,
где i
–
номер строки,
,
где i
–
номер строки,
или
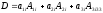 ,
где j
– номер столбца.
,
где j
– номер столбца.
Пример. Вычислить определитель разложением по элементам:
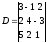
 1)
второй строки; 2) третьего столбца.
1)
второй строки; 2) третьего столбца.
Решение:
1)
i
=2,
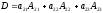 .
.
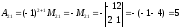 .
.
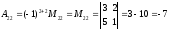 .
.
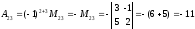 .
.
 .
.
2)
i
= 3,
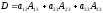 .
.
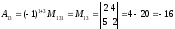 .
.
 .
.
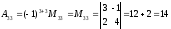 .
.
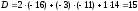 .
.
Ответ:
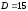 .
.
1.3. Решение систем линейных уравнений методом определителей (метод Крамера)
Рассмотрим систему трех линейных уравнений с тремя неизвестными: x1, x2, x3:
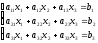
(коэффициенты aij и свободные члены bi считаются заданными).
Решение:
составим определители
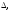
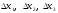 :
:
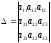 ,
,
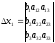 ,
,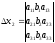 ,
,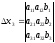 ,
,
где называют определителем системы, а определители xi получены из основного определителя заменой свободными членами bi элементов соответствующего столбца.
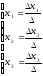
Особые случаи:
1) если 0, то система имеет единственное решение;
2) если = 0, xi 0, то система несовместна;
3) если = xi = 0, то система либо имеет бесконечное множество решений, либо она решений не имеет.
Пример.
Решить
систему линейных уравнений:
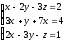
Решение: составим определители , x, y, z и найдем их значения.
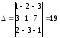 (
0, следовательно, система имеет единственное
решение).
(
0, следовательно, система имеет единственное
решение).
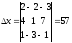 .
.
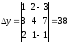 .
.
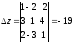 .
.
Найдем
решение системы: 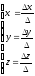
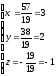
Ответ: (3; 2; –1).
II. Аналитическая геометрия
2.1. Координаты вектора в пространстве. Действия над векторами в координатной форме
Пусть
M(x; у; z) – координаты точки в пространстве.
Выберем:
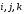 –
единичные векторы на соответствующих
осях координат:
–
единичные векторы на соответствующих
осях координат:
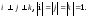
Всякий
вектор пространства можно представить
в виде линейной комбинации единичных
векторов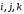 :
:
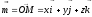 ,
,
где
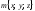 – координаты вектора в пространстве.
– координаты вектора в пространстве.
Длина
вектора
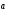 вычисляется по формуле
вычисляется по формуле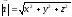 .
.
Рассмотрим
две точки пространства:
 и
и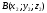
Найдем
координаты вектора
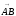 :
: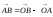 .
.
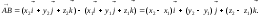
Таким
образом,
 – координаты вектора
– координаты вектора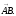
Длина
вектора
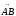 определяется по формуле
определяется по формуле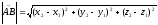 .
.
Справедливо следующее утверждение:
пусть:
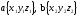 и
и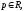 тогда
тогда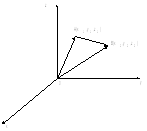
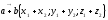

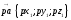 .
.
Пример 1.
Найти расстояние между точками А и В, если известно, что А(–2;3;1) и В(2;1;5).
Решение:
1.
Найдем координаты вектора
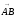 :
:
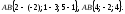
2.
Вычислим длину вектора
 :
: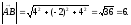
Ответ: 6.
Пример 2.
Найти
длину вектора
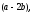 если
если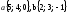 .
.
Решение:
1.
Обозначим:
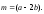
2.
Найдем координаты вектора

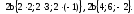
3.
Найдем координаты вектора
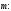
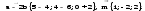
4.
Вычислим длину вектора
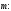
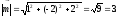
Ответ: 3.
2.2. Скалярное произведение векторов. Угол между векторами
Скалярным
произведением
двух векторов
 и
и называется произведение модулей этих
векторов на косинус угла между ними.
называется произведение модулей этих
векторов на косинус угла между ними.
Обозначение: 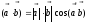
Особые случаи:
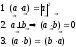
Если
векторы
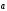 и
и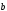 заданы своими координатами:
заданы своими координатами: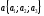 и
и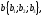 то скалярное произведение вычисляется
по формуле:
то скалярное произведение вычисляется
по формуле: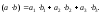
Угол между векторами выражается следующим образом:
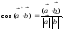
В
координатной форме: 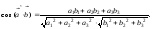
Пример 3.
Найти
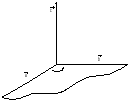
угол между векторами
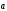 и
и ,
если
,
если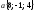 и
и
Решение:
Обозначим:
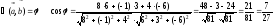 .
.
Ответ: