
- •Глава 1
- •1.1. Схема обобщенной электрической цепи
- •1.2. Основные понятия электрической цепи
- •1.3. Основные законы электрических цепей
- •Глава 2
- •2) По математическому представлению все многообразие радиотехнических сигналов принято делить на две основные группы: детерминированные (регулярные) и случайные сигналы (рис. 2.2).
- •3. Векторное представление – это представление сигнала вектором на комплексной плоскости. При расчетах удобно использовать следующие понятия о гармоническом сигнале.
- •2.3. Спектральное представление сигналов
- •2.4. Операторное представление сигнала
- •2.6.1. Амплитудная модуляция
- •2.6.2. Угловая модуляция
3. Векторное представление – это представление сигнала вектором на комплексной плоскости. При расчетах удобно использовать следующие понятия о гармоническом сигнале.
а) Комплексное гармоническое колебание – гармонический комплекс:
s (t)
= Аm
e j(ωt+φ)
= Am
e jωt,
(t)
= Аm
e j(ωt+φ)
= Am
e jωt,
г де
e jωt
– множитель вращения. На комплексной
плоскости гармонический комплекс
представляется вектором Аm
c начальной фазой φ0,
вращающимся против часовой стрелки с
частотой ω.
де
e jωt
– множитель вращения. На комплексной
плоскости гармонический комплекс
представляется вектором Аm
c начальной фазой φ0,
вращающимся против часовой стрелки с
частотой ω.
б) Гармоническое колебание s(t) = Amcos(ωt+φ0) = Re{Am e jφ}. На комплексной плоскости гармоническое колебание представляется проекцией вращающегося с частотой ω против часовой стрелки вектора гармонического комплекса на реальную ось (рис. 2.10).
в )
Комплексная амплитуда
)
Комплексная амплитуда
![]() .
На комплексной плоскости она представляется
в виде неподвижного вектора с амплитудой
Am
и начальной фазой 0.
.
На комплексной плоскости она представляется
в виде неподвижного вектора с амплитудой
Am
и начальной фазой 0.
Спектральное и операторное представление сигнала рассмотрим подробнее в разд. 2.3 и 2.4.
2.3. Спектральное представление сигналов
Очень часто математическое описание даже несложных по структуре детерминированных сигналов является весьма трудной задачей. Поэтому в теории электрических цепей и радиоэлектронике используется оригинальный прием, при котором реальные сигналы заменяют (аппроксимируют) набором идеализированных математических моделей, описываемых простыми функциями. Это дает важный инструмент для анализа прохождения сигналов через радиотехнические цепи. Подобным образом можно также упростить задачу синтеза сложных сигналов из совокупности простых сигналов.
Спектральный способ представления сигнала s(t) основан на представлении любой функции времени совокупностью гармонических составляющих с соответствующими амплитудами, частотами и начальными фазами. При спектральном представлении сигнал задается не как функция времени, а как функция частоты, что является очень удобным, поскольку свойства электрических цепей часто задаются их частотными характеристиками.
Спектры периодических сигналов
Сигналы, удовлетворяющие условию s(t) = s(t+T), если Т < ∞, а –∞<t<+∞ называются периодическими. Простейшим периодическим сигналом является гармоническое колебание s(t) = Amcos(ω0t+0).
Из математики известно, что любой периодический сигнал s(t), удовлетворяющий условиям Дирихле, может быть представлен тригонометрическим рядом Фурье
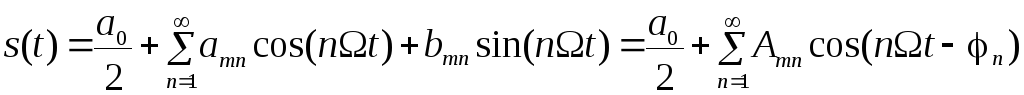 ,
,
где
![]() – основная частота следования сигнала
(первая гармоника сигнала), n
– номер гармоники сигнала, nΩ
– частота n-й гармоники
сигнала,
– основная частота следования сигнала
(первая гармоника сигнала), n
– номер гармоники сигнала, nΩ
– частота n-й гармоники
сигнала,
![]() – коэффициенты ряда Фурье:
– коэффициенты ряда Фурье:
 – постоянная (средняя) составляющая
сигнала;
– постоянная (средняя) составляющая
сигнала;
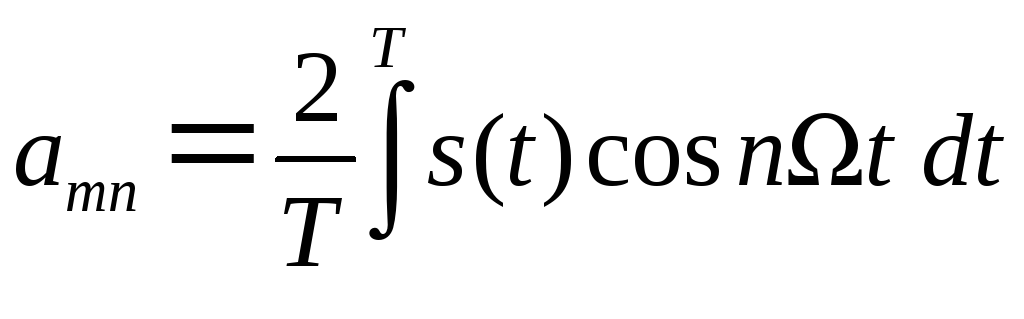 – амплитуда n-й косинус
составляющей спектра сигнала;
– амплитуда n-й косинус
составляющей спектра сигнала;
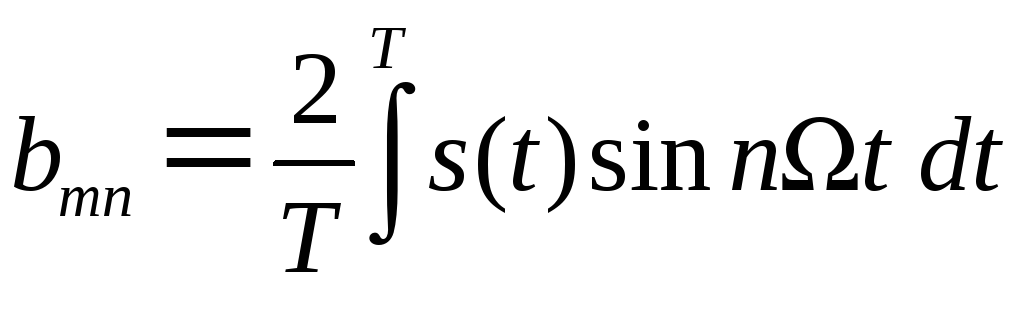 – амплитуда n-й синус
составляющей спектра сигнала;
– амплитуда n-й синус
составляющей спектра сигнала;
![]() – амплитуда n-й
гармоники;
– амплитуда n-й
гармоники;
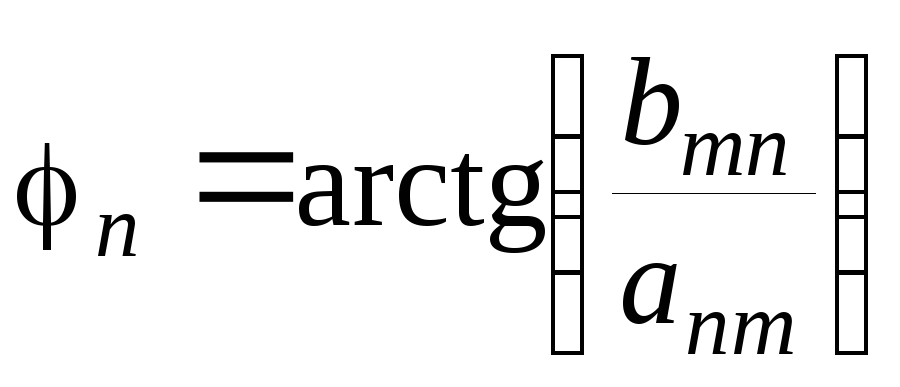 – начальная фаза n-й
гармоники.
– начальная фаза n-й
гармоники.
Из ряда Фурье следует, что спектр периодического сигнала имеет дискретный (линейчатый) характер по оси частот (рис. 2.11).
Д
АЧС
а а б б 2 3 4 5 АЧС ФЧС ФЧС 0 0 0 n Amn Am1 Am2 Am3 Am 0 0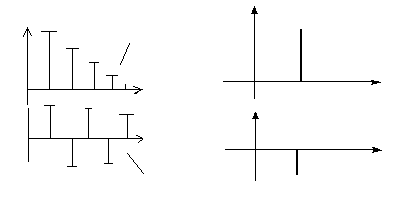
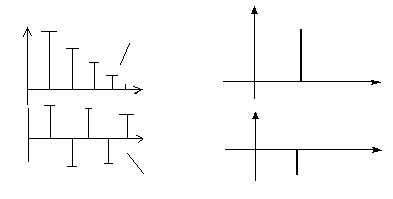
Рис. 2.11 Рис. 2.12
Амплитудным, или амплитудно-частотным, спектром (АЧС) называется зависимость амплитуд гармонических составляющих от частоты (АЧС → Amn(ω), рис 2.11, а).
Фазово-частотным спектром (ФЧС) называется зависимость начальных фаз гармонических составляющих от частоты (ФЧС → (ω), рис. 2.11, б).
Спектр гармонического колебания состоит из одной гармонической составляющей с амплитудой Am (рис. 2.12, а) и фазовым сдвигом 0 на частоте ω0 (рис. 2.12, б).
Спектры непериодических сигналов
Для проведения гармонического анализа непериодических колебаний представим их в виде периодических, с бесконечно большим периодом (T→∞). Устремляя период к бесконечности в пределе, получим:
1) Основная частота
следования
![]() =
=![]() → 0. Это означает, что расстояние
между спектральными линиями, равное
основной частоте следования
→ 0. Это означает, что расстояние
между спектральными линиями, равное
основной частоте следования
![]() ,
становится бесконечно малым, а спектр
– сплошным.
,
становится бесконечно малым, а спектр
– сплошным.
2)
![]() ,
т. е. спектр состоит из гармонических
составляющих с бесконечно малыми
амплитудами.
,
т. е. спектр состоит из гармонических
составляющих с бесконечно малыми
амплитудами.
Поэтому спектр непериодического сигнала характеризуется функцией спектральной плотности. Она показывает плотность распределения бесконечно малых амплитуд по оси частот, т.е. показывает, сколько гармонических составляющих с бесконечно малыми амплитудами приходится в диапазон частот df.
Функция спектральной плотности S(jω) связана с сигналом s(t) через преобразование Фурье:
![]() – прямое преобразование Фурье (ППФ).
– прямое преобразование Фурье (ППФ).
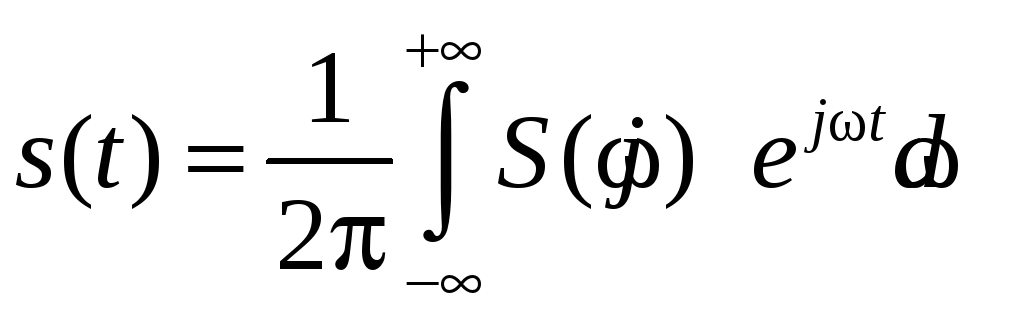 – обратное преобразование Фурье (ОПФ).
– обратное преобразование Фурье (ОПФ).
Функция спектральной плотности – это комплексная функция частоты
S(jω) = S(ω)e jφ(ω),
где S(ω) – модуль функции спектральной плотности, его называют спектральной плотностью амплитуд, φ(ω) – аргумент функции спектральной плотности – спектр фаз.
Главной особенностью спектра непериодического сигнала является его сплошной непрерывный характер.
Пример. Найти S(jω) одиночного прямоугольного импульса (рис. 2.13).
П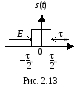 о
временной диаграмме запишем аналитическое
выражение такого сигнала:
о
временной диаграмме запишем аналитическое
выражение такого сигнала:
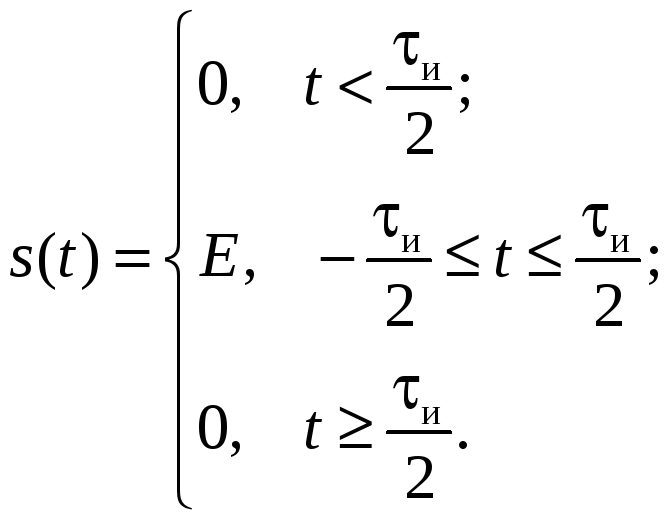 .
.
Найдем функцию спектральной плотности импульса и приведем это выражение к функции типа (sin x/x).
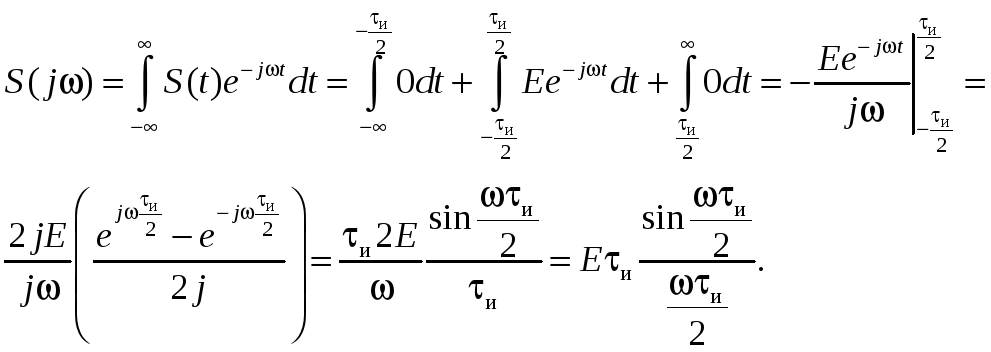
![]()
Амплитудная спектральная плотность импульса (рис. 2.14) имеет вид
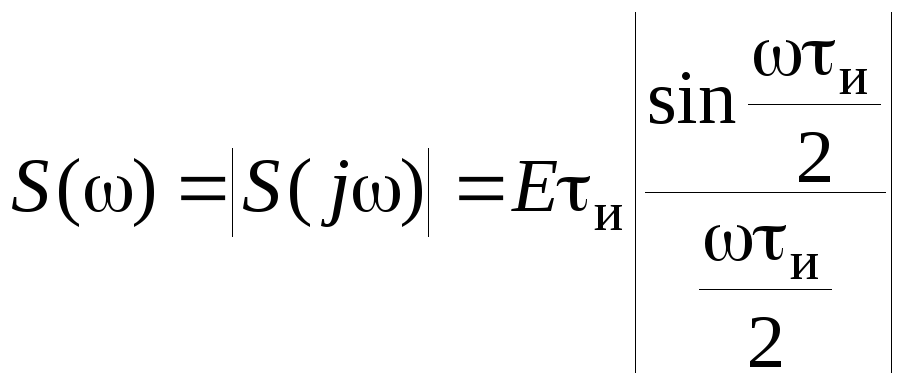 .
.
Б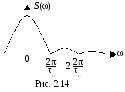 ольшинство
сигналов имеет бесконечный частотный
спектр. В то же время для них применяют
понятие о ширине спектра, т.е. считают,
что спектры у таких сигналов ограничены.
Под шириной спектра понимают диапазон
частот, в котором сосредоточена заданная
доля от энергии всего сигнала 50, 90, 95, …
% .
ольшинство
сигналов имеет бесконечный частотный
спектр. В то же время для них применяют
понятие о ширине спектра, т.е. считают,
что спектры у таких сигналов ограничены.
Под шириной спектра понимают диапазон
частот, в котором сосредоточена заданная
доля от энергии всего сигнала 50, 90, 95, …
% .
Для одиночного прямоугольного импульса за ширину спектра принимают интервал частот от 0 до 2/τи, т.е. граничная частота верхняя гр = 2/τи .
Следовательно, чем короче импульс τи, тем шире его спектр гр.
