Глава 2

Математические модели сигналов

Переменные ток и напряжение называются электрическими коле­баниями и описываются функцией времени s(t). Колебание, ото­бражающее передаваемое сообщение или информацию о состоянии исследуемого объекта, называется сигналом, который может быть описан некоторой функцией:

1) – временная функция.

2) – пространственно-временная функция.

В дальнейшем будем рассматривать лишь временные сигналы.

2.1. Классификация электрических сигналов

1) По характеру их изменения во времени и по величине.

Сигналы разделяются на непрерывные (аналоговые) и импульсные.

Аналоговый сигнал описывается функцией, произвольной по величине и непрерывной во времени.

Импульсные сигналы – это сигналы, существующие не на всей временной оси, или эти сигналы описываются функциями с разрывами.

Импульсные сигналы подразделяются на следующие:

1) дискретные,

2) квантованные,

3) цифровые.

На рис. 2.1 показаны временные диаграммы аналогового, дискретного, квантованного и цифрового сигналов.

На рис. 2.1, а приведен фрагмент аналогового сигнала.

Дискретный сигнал (рис. 2.1, б). Это сигнал, произвольный по величине и дискретный во времени.

При дискретизации непрерывный сигнал заменяется своими отсчетами – S(nΔt), взятыми с шагом Δt (шаг дискретизации).

Для того чтобы непрерывный сигнал дискретизировать, а затем по этим отсчетам восстановить исходный аналоговый сигнал, шаг дискретизации ∆t должен удовлетворять следующему условию:

,

где F_max – максимальная частота в исходном аналоговом сигнале. Это соотношение называется теоремой Котельникова.

Квантованный сигнал (рис. 2.1, в). Это сигнал, непрерывный во времени, но дискретный по величине. Для его получения ось значений сигнала разбивают на фиксированные уровни (уровни квантования). При квантовании мгновенным значениям аналогового сигнала ставят в соответствие ближайший разрешенный уровень. ∆x – шаг квантования (∆x = x_n+1 – x_n). Величину шага квантования выбирают исходя из величины помехи, которая, накладываясь на исходный сигнал, искажает его форму. Чтобы искажений вследствие помех не было, шаг квантования выбирают из соотношения:

.

Цифровые сигналы (рис. 2.1, г). Это сигналы, квантованные по величине и дискретные во времени. Передача такого сигнала заменяется передачей цифр, соответствующих уровням квантования в дискретные моменты времени.

2) По математическому представлению все многообразие радиотехнических сигналов принято делить на две основные группы: детер­минированные (регулярные) и случайные сигналы (рис. 2.2).

й

й

й

й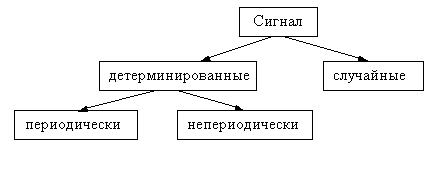

Рис. 2.2

Детерминированные сигналы задаются некоторой аналитической функцией времени s(t). С точки зрения передачи информации, такой сигнал никакой информации не несет, поскольку для любого момента времени t₁ можно заранее подсчитать значение сигнала s(t₁). Такие сигналы применяются:

- как управляющие сигналы в различных системах управления;

- как испытательные в устройствах выделения информации для определения их характеристик. Проходя через цепь, сигнал искажается. По искажениям сигнала можно оценивать свойства устройства, т.е. испытывать (определять) характеристики устройства.

Детерминированные колебания делятся на периодические и непериодические. Периодическим считается такое колебание, кото­рое повторяется через одинаковые промежутки времени: s(t) = s(t + Т), Т – период колебания.

Примеры периодических сигналов.

1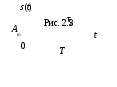) Периодическая последовательность прямоугольных импульсов (рис. 2.3). Ее параметры: A_m – амплитуда; – длительность импульса. Это пример импульсного сигнала.

2) Гармонические колебания (рис. 2.4).

s(t) = A_mcos(t – ₀).

Его параметрами являются: A_m – амплитуда,  – частота, ₀ – начальная фаза. Это пример непрерывного сигнала.

Непериодические сигналы – это сигналы, которые описываются непериодическими функциями времени. Однако их можно рассматривать как периодические, для которых Т .

Примеры непериодических сигналов.

1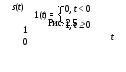) Сигнал типа «единичная функция» (ступенчатый сигнал, функция Хевисайда (рис. 2.5)).

2) Одиночный прямоугольный импульс – это сигнал, форма которого прямоугольная (рис. 2.6).

3) Сигнал типа  (дельта-функция, функция Дирака (рис. 2.7)).

Он обладает свойствами:

1) ;

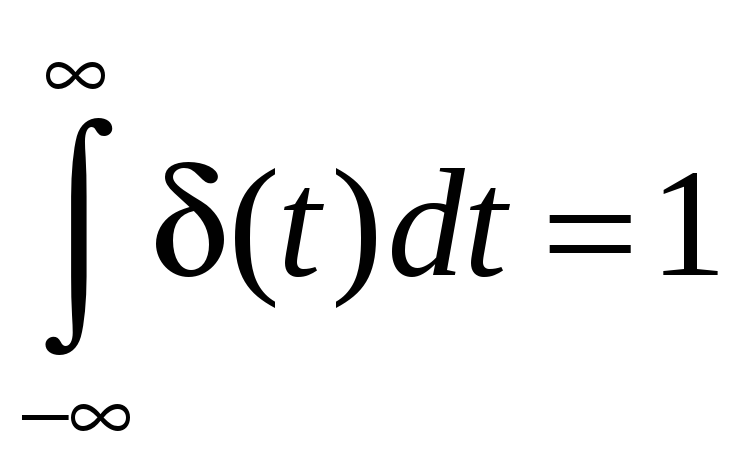2) .

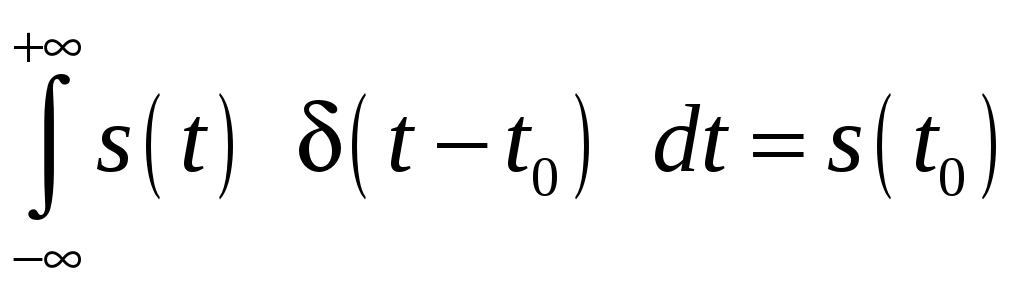Это соотношение называют фильтрующим свойством дельта-функции.

Случайные сигналы – это сигналы, характер изменения которых заранее предсказать невозможно. Именно эти сигналы несут новую информацию о состоянии интересующего нас объекта. С математической точки зрения, эти сигналы описываются методами теории вероятности или случайных процессов. Разновидностью случайных сигналов являются помехи – сигналы, которые накладываются на передаваемые сообщения и искажают его характер. Помехи бывают атмосферными, индустриальными и флуктуационными.

Флуктуационные помехи связаны с процессами, происходящими в элементах электрических цепей, а именно с движением свободных носителей зарядов в них.

2.2. Гармоническое колебание и способы его представления

Гармоническим называется колебание, которое описывается гармонической функцией времени: sin(t), cos(t).

Гармоническое колебание, а также сигнал произвольной формы могут быть представлены в следующих формах:

- временное представление сигнала;

- комплексное представление;

- векторное представление;

- спектральное;

- операторное.

1. При временном представлении сигнал записывается в виде аналитической функции времени:

.

Его график называется временной диаграммой (рис. 2.8.). Основными параметрами гармонического сигнала являются:

1) Амплитуда A_m (наибольшее отклонение от нуля гармонической функции). Размерность амплитуды связана с физической природой сигнала.

2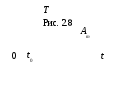) Период T (минимальное расстояние между точками, находящимися в одной фазе), ω = 2π/T – круговая частота, f = 1/T – частота. Их размерность: T  [с]; f  [Гц]; ω  [рад/с].

3) ₀ = ωt₀ – начальная фаза гармонического колебания; t₀ – временной сдвиг, если t₀ > 0, это означает опережение, если t₀ < 0, это означает задержку сигнала относительно сигнала с t₀ = 0.

4) Ψ(t) = (ωt + φ₀) – полная фаза гармонического колебания.

5) ω(t) = dΨ(t)/dt – мгновенная частота.

2. При комплексном представлении гармоническое колебание как функция времени заменяется комплексной амплитудой, т.е. комплексным числом, не зависящим от времени. Это делается для упрощения записи и выполнения операций над гармоническими функциями.

Вспомним комплексные числа. Z – комплексное число. Его можно записать в одной из трех форм: алгебраической, показательной и тригонометрической.

Z = a + jb = ,

где a = Re [Z] = A cos ; b = Im[Z] = A sin.

R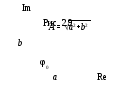e – реальная часть, Im – мнимая часть комплексного числа. На рис. 2.9 показано геометрическое представление комплексного числа на комплексной плоскости.

А – mod[Z] – модуль комплексного числа Z, или А = (а²+b²)^1/2 – длины векторов комплексного числа.

φ = arg[Z] – аргумент комплексного числа Z, или φ = arctg(b/a) – начальная фаза.

Выражение А_me^j(ωt+φ) называют комплексом гармонической функции. Тогда, учитывая, что Аcosφ = Re{Ae^jφ}, можно записать

.

Комплексную величину называют комплексной амплитудой гармонического сигнала, а е^jωt – множителем вращения. Комплексная амплитуда содержит информацию о двух важнейших параметрах гармонического сигнала – об амплитуде и начальной фазе. Комплексная амплитуда и гармоническая функция времени при известной частоте ω связаны взаимноодно- значно, т.е.

.

Например, гармоническому колебанию u(t) = 256 cos(2π100t – 45) соответствует комплексная амплитуда _m = 256 e^–j45. Справедливо и обратное.