
Физика-лекции
.pdf
Пример 4. Вычислить момент инерции стержня, массы m, длины l относительно перпендикулярной ему оси, проходящей через его конец.
Рассуждения аналогичные предыдущему примеру.
l |
l |
m |
|
m |
|
x |
3 |
|
l |
|
m |
|
l |
3 |
|
1 |
|
|
|
|
|
|
|
|
|||||||||||
J001 x2dm x2 |
dx |
|
|
|
|
|
|
|
ml 2 . |
||||||||
l |
l 3 |
|
0 |
l 3 |
|
||||||||||||
0 |
0 |
|
|
|
|
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Анализируя примеры 3 и 4, приходим к выводу: момент инерции тела зависит от выбора оси вращения. Момент инерции относительно произвольной оси можно вычислить, применяя теорему Штейнера.
Теорема Штейнера: Момент инерции тела относительно произвольной оси равен сумме J0 момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:
J J0 md 2 .
Пример 5. Рассмотрим пример 4 с применением теоремы Штейнера:
|
2 |
|
1 |
|
2 |
l |
2 |
1 |
|
2 |
|
ml 2 |
|
4 |
|
2 |
|
1 |
|
2 |
|
||||||
J J 0 md |
|
|
|
|
ml |
|
m |
|
|
|
|
|
ml |
|
|
|
|
|
|
ml |
|
|
|
|
ml |
|
. |
|
12 |
|
|
12 |
|
4 |
12 |
|
3 |
|
|||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Вычисление оказалось гораздо проще и быстрее.
Таблица значений моментов инерции для некоторых однородных тел.
Тело |
Положение оси вращения |
Момент |
|||||||
|
|
инерции |
|||||||
|
|
|
|
|
|
|
|
|
|
Полый тонкостенный |
Ось симметрии |
|
|
|
mR2 |
||||
цилиндр, обруч |
|
|
|
|
|
|
|
|
|
Однородный диск |
Ось симметрии |
|
|
|
mR 2 |
|
|||
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
||
|
Ось, проходящая через край |
|
3 |
|
mR 2 |
||||
|
|
2 |
|||||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
Прямой тонкий стержень |
Ось проходит через середину |
|
1 |
ml 2 |
|||||
|
|
12 |
|||||||
|
|
|
|
||||||
|
|
|
|
|
|
||||
|
Ось проходит через конец |
|
|
1 |
ml 2 |
||||
|
|
|
|
|
|||||
|
|
3 |
|
|
|||||
|
|
|
|
|
|||||
Шар |
Ось проходит через центр шара |
|
2 |
mR 2 |
|||||
|
|
5 |
|||||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
31

§ 3. Момент силы
|
|
|
|
|
|
|
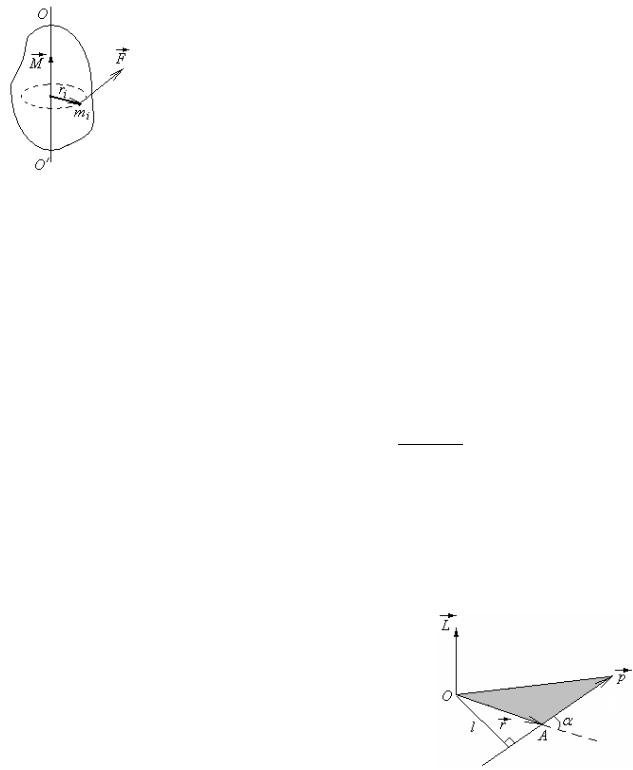
Моментом силы F относительно неподвижной |
|
|
|
|
||
точки О называется векторная физическая величина, |
|
|
|
|
||
определяемая векторным произведением радиус-вектора |
|
|
|
|
||
|
|
|
|
|
|
|
r , проведенного из точки О в точку А приложения силы, |
|
|
|
|
||
|
|
|
|
|
|
|
на силу F : |
|
|
|
|
|
|
|
|
|
|
|
|
|
M r , F . |
|
|
|
|
||
Момент силы - псевдовектор, его направление совпадает |
с |
направлением |
||||
поступательного движения правого винта при его вращении от |
|
к |
|
(по правилу |
||
r |
F |
|||||
правого винта).
Модуль момента силы: M rF sin F l ,
где - угол между радиус-вектором и силой, l r sin - плечо силы - кратчайшее расстояние между линией действия силы и точкой О.
Измеряется момент силы в системе СИ: [M]=Н м.
Моментом силы относительно неподвижной оси Z
называется скалярная физическая величина, равная проекции |
|||
|
|
|
|
на эту ось вектора |
момента силы |
M , определенного |
|
относительно произвольной точки О данной оси Z: |
|||
|
|
|
|
M z |
(M )z |
[r , F]z M cos , |
|
где - угол между вектором момента силы и осью Z.
Пусть тело вращается вокруг оси Z под действием силы F .
Плоскость, перпендикулярная оси вращения, проходящая через точку приложения силы, называется плоскостью вращения. Точка приложения силы описывает окружность радиуса R.
|
|
|
|
Рассмотрим подробнее, какая сила |
||||
|
|
|
приводит |
к |
вращению. |
Выберем |
||
|
|
|
произвольную точку |
твердого |
тела, к |
|||
|
|
|
|
|
|
|
|
|
которой приложена сила |
F . |
|
|
|
||||
|
Разложим |
эту |
силу |
на |
составляющие: |
|||
|
|
|
|
|
|
|
|
|
F |
F Fn F . |
|
|
|
|
|
||
|
Момент |
этой |
||
|
|
|
|
|
M [r , F] [r , (F|| F
силы |
относительно |
точки О: |
|
|
|
|
|
F )] [r , F|| ] [r , F ] [r , F ] .
Момент |
|
силы |
|
относительно |
оси |
Z: |
|
||
|
|
|
|
|
|
|
|
||
M z (M|| ) z |
|
(M ) z |
(M ) z . |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Но M || |
и M |
перпендикулярны оси Z, |
а проекция перпендикуляра на ось |
||||||
равна нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где rcos =R. |
|
|
|
M z |
(M )z M z cos rF sin cos RF , |
||||||
32
Таким образом, из трех составляющих силы F вращение вокруг оси Z может
вызвать только касательная составляющая F .
Вращательным моментом называется момент силы относительно оси способный силы вращать тело вокруг оси.
§ 4. Уравнение динамики вращательного движения
Представим вращающееся тело как совокупность вращающихся элементарных масс mi, находящихся на расстоянии ri от оси вращения ОО1.
Все точки тела имеют одинаковые угловые скорости и ускорения , но разные линейные скорости V и ускорения а.
|
|
|
|
|
|
|
Ускорение аi материальной точки массой mi |
вызывается |
|||
|
|
|
|
|
|
силой |
Fi . По второму закону Ньютона Fi mi ai . Касательная |
||||
|
|
|
|
|
|
составляющая силы вызывает касательное ускорение: |
F |
a . |
|||
Учитывая связь |
между линейными |
и угловыми |
характеристиками: |
||
Vi ri , a i ri запишем:
Fi mi ri .
Умножим обе части равенства на ri:
Fi ri
M i
mi r 2i .
Ji
Для всего твердого тела просуммируем все элементы массы:
Fi ri mi ri 2 ; |
|
|
|
||
M J . |
|
|
|
||
В общем случае запишем в векторном виде: |
|
|
|
|
. |
|
|
||||
|
M J |
|
|||
Основной закон динамики вращательного движения (второй закон Ньютона для вращательного движения): Суммарный момент сил, приложенных к телу, равен произведению момента инерции на угловое ускорение.
Сравним с уравнением динамики поступательного движения: F ma . Роль силы при вращательном движении играет момент силы. Роль массы - момент инерции.
§ 5. Момент импульса
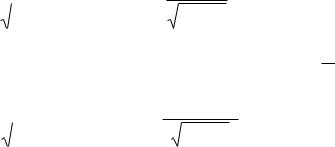
Моментом импульса материальной точки А
относительно неподвижной точки О называется векторная физическая величина, определяемая векторным произведением:
L [r , p] [r , mV ] ,
где r радиус-вектор, проведенный из точки О в точку А, материальной точки.
|
|
- импульс |
p mV |
||
33

|
- псевдовектор, его направление определяется по правилу правого винта: |
|
L |
L |
совпадает с направлением поступательного движения правого винта при его
|
|
|
|
|
вращении от r к |
p .. |
|
|
|
Модуль момента импульса |
L : L r p sin p r sin p l , |
|||
где l - плечо вектора |
|
относительно точки О, - угол между радиусом-вектором и |
||
p |
||||
импульсом.
Моментом импульса относительно неподвижной оси Z называется скалярная физическая величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси.
При вращении абсолютно твердого тела вокруг неподвижной оси Z каждая
отдельная точка тела движется по окружности постоянного радиуса r |
с некоторой |
||||||
|
|
|
|
|
|
i |
|
|
|
|
|
||||
скоростью |
Vi . Скорость |
Vi |
и импульс |
pi miVi |
перпендикулярны этому радиусу, |
||
т.е. радиус является плечом импульса. Поэтому для отдельной i-ой частицы момент импульса: Liz miVi ri .
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:
n
Lz miVi ri .
i 1
Используя связь между линейными и угловыми характеристиками: Vi ri получим:
n |
n |
|
Lz mi ri |
2 mi ri |
2 J z |
i 1 |
i 1 |
|
|
Lz J z . |
|
Таким образом, момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.
§ 6. Закон сохранения момента импульса
Продифференцируем уравнение: Lz=Jz по времени, считая Jz=const.
|
dLz |
J |
|
d |
J |
|
M |
|
|
|
|
dLz |
M |
|
|
|
|
z |
|
z |
z |
|
|
|
z |
||||||
|
dt |
dt |
|
|
|
dt |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
dL |
|
|
|
||
Или в векторном виде, что тоже имеет место: |
|
M |
|
|
|||||||||||
dt |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.
Рассмотрим систему тел. Если момент внешних сил для нее будет равен нулю: |
||
M 0 |
, то |
|
dL 0 L const |
||
|
|
|
dt
34
Это и есть закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени.
Продемонстрировать этот закон можно с помощью скамьи Жуковского. Пусть человек, находящийся на скамье, которая без трения вращается вокруг вертикальной оси с угловой скоростью 1, держит на вытянутых руках гантели. Если человек прижмет гантели к себе, то момент инерции системы уменьшится J1>J2. Поскольку момент внешних сил равен нулю, то по закону сохранения момента импульса:
J1 1 |
J 2 2 |
угловая скорость системы возрастает. Отсюда: 2 |
1, причем: |
||
J1 |
|
2 . |
|
|
|
|
|
|
|
||
J |
2 |
|
|
|
|
|
|
1 |
|
|
|
Аналогично акробат во время прыжка через голову поджимает к туловищу руки и ноги, чтобы уменьшить свой момент инерции и увеличить тем самым угловую скорость вращения.
35

Глава 1.5. ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
§1. Принцип относительности Галилея
Вклассической механике справедлив принцип относительности Галилея:
законы динамики одинаковы во всех инерциальных системах отсчета.
Для доказательства рассмотрим две инерциальные системы отсчета К и К'.
Система К неподвижна, а К |
движется |
относительно системы К равномерно и |
|
прямолинейно со скоростью |
|
const . |
Отсчет времени начнем с момента, когда |
V0 |
|||
начала координат этих систем (точки О и О') совпадают. Рассмотрим частный случай, когда оси координат z и z, y и y параллельны, т.е. z=z , y=y , тогда координаты x и x произвольной точки Р будут связаны уравнением: x x V0t .
 .
.
В классической механике предполагается, что время во всех системах отсчета течет одинаково: t=t. Добавим это уравнение к преобразованиям координат:
x x V0t; y y ; z z ; t t .
Эти 4 уравнения называют преобразованиями Галилея. Они позволяют перейти от координат и времени одной инерциальной системы отсчёта к
координатам и времени другой инерциальной системы отсчёта. |
|
|||||||
|
Продифференцируем все уравнения системы по времени: |
|
||||||
|
|
Vx Vx V0 ; Vy Vy ; Vz Vz . |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Или в векторном виде: |
V |
V |
V0 |
|
. Это – формула преобразования скорости |
||
при переходе от системы К к системе К , или закон сложения скоростей. |
||||||||
|
|
|
|
|
|
|
|
|
|
Если продифференцируем еще раз, то получим: a |
a . |
|
|||||
|
Следовательно, если на точку Р другие тела не действуют, то |
|||||||
|
a 0, а значит и |
|||||||
, т.е. система К является инерциальной. |
|
|
||||||
a 0 |
|
|
||||||
Таким образом, мы подтвердили механический принцип относительности:
законы динамики при переходе от одной инерциальной системы отсчета к другой не изменяются, т.е являются инвариантными (invariantis - неизменный) по отношению к преобразованиям координат. Другая формулировка принципа относительности Галилея: уравнения динамики инвариантны по отношению к преобразованиям Галилея.
36
§ 2. Постулаты специальной теории относительности СТО
Классическая механика Ньютона прекрасно описывает движение макротел, движущихся с малыми скоростями V с .
Но в конце XIX века был обнаружен ряд противоречий между классической теорией и экспериментом. Было установлено, что движение быстрых заряженных частиц не подчиняется законам механики. Возникли затруднения при попытках применить механику Ньютона к объяснению распространения света. Так опыт Майкельсона-Морли (американские ученые) показал, что скорости света в двух движущихся друг относительно друга системах равны, что противоречило правилу сложения скоростей классической механики. Одновременно было обнаружено противоречие между классической теорией и уравнениями Максвелла, лежащими в основе понимания света как электромагнитной волны.
Для объяснения этих и некоторых других опытных данных необходимо было создать новую теорию. Это удалось сделать А. Эйнштейну. Он заложил основы специальной теории относительности, которую часто называют релятивистской теорией.
В основе специальной теории относительности (СТО) лежат два постулата Эйнштейна, сформулированные им в 1905 году:
1) Принцип относительности: все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой.
Эйнштейн распространил механический принцип относительности Галилея на все без исключения физические явления (механические, электрические, оптические). Согласно первому постулату Эйнштейна любые явления во всех инерциальных системах отсчета протекают одинаково.
2) Принцип постоянства скорости света: скорость света в вакууме одинакова во всех инерциальных системах отсчета.
Доказательство этого принципа было получено в 1887 году в опытах
Майкельсона и Морли. Скорость света в вакууме с 3 108 м / с является предельной. Никакой сигнал не может распространяться со скоростью, превышающей скорость света.
СТО потребовала отказа от привычных представлений о пространстве и времени. Потеряло смысл не только абсолютное пространство, но и абсолютное время.
Постулаты Эйнштейна и теория, построенная на их основе, установили новый взгляд на мир и новые пространственно-временные представления, такие, например, как относительность длин и промежутков времени, относительность одновременности событий. Эти и другие утверждения находят надежное экспериментальное подтверждение.
§ 3. Преобразования Лоренца
Рассмотрим две инерциальные системы отсчета: К и К (рис. из §1). Система К неподвижна, а К движется относительно системы К вдоль оси Х со скоростью V . Пусть в начальный момент времени, когда начала координат О и О' совпадают,
37
излучается световой импульс. Согласно второму постулату Эйнштейна, скорость света в обеих системах одинакова и равна с.
За время t в системе К сигнал дойдет до точки Р, пройдя расстояние: x ct .
В системе К координата светового импульса в момент достижения точки Р:
|
x ct . |
Вычитая, получим: |
x x c(t t) . |
Так как x x (система К перемещается по отношению к системе К), то t t , т.е. отсчет времени имеет относительный характер (в классической физике
считается, что время во всех инерциальных системах отсчета течет одинаково, т.е. t t ).
Анализ явлений в инерциальных системах отсчета, проведенный А.Эйнштейном на основе сформулированных им постулатов, показал, что классические преобразования Галилея несовместимы с ними. Необходимы другие преобразования, удовлетворяющие постулатам СТО.
Более общие преобразования, удовлетворяющие постулатам Эйнштейна, предложил Лоренц в 1904 г.
Преобразования Лоренца имеют вид:
К К К К
|
x Vt |
|
|
|
|
|
||||
x |
|
|
|
|
|
|
|
, |
||
|
|
|
|
|
|
|
||||
1 |
2 |
|
||||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
y y, |
|
|
|
|
|
|
||||
z z, |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||
t |
t Vx / c |
|
|
, |
||||||
|
|
|
|
|||||||
|
|
1 2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
x x Vt ,1 2
y y ,z z ,
t Vx / c2
t
1 2
где Vc
,
Уравнения симметричны и отличаются лишь знаком при V . Это очевидно. Если система К' движется относительно системы К со скоростью V , то скорость движения системы К относительно системы К' равна (-V ).
При малых скоростях V c , 1 преобразования Лоренца переходят в классические преобразования Галилея. При скоростях V c выражения x,t, x ,t теряют физический смысл, что находится в соответствии с утверждением: движение со скоростью, большей скорости распространения света в вакууме невозможно.
В преобразованиях Лоренца устанавливается взаимосвязь пространства и времени (в закон преобразования координат входит время, а в закон преобразования времени – пространственные координаты). Таким образом, теория Эйнштейна использует четырехмерное пространство - время.
38

§ 4. Следствия из преобразований Лоренца
Из преобразований Лоренца можно получить следствия, казалось бы, противоречащие нашему повседневному опыту. Однако наш опыт относится лишь к процессам, протекающим со скоростями весьма малыми по сравнению со скоростью света (V c ). Явления, которые мы сейчас рассмотрим, присущи миру элементарных частиц, в котором движение происходит со скоростями, близкими к скорости света.
1. Относительность понятия одновременности в разных системах отсчёта
Пусть в системе К в точках с координатами x1 и x2 в моменты времени t1 и t2 |
|||
происходят два события. |
В системе К' им соответствуют координаты x и |
x и |
|
|
|
1 |
2 |
моменты времени t |
и t |
. Если события в системе К происходят в одной точке |
|
1 |
2 |
|
|
(x1=x2) и являются одновременными (t1=t2), то согласно преобразованиям Лоренца:
x |
x |
и t t |
, |
|
1 |
2 |
1 |
2 |
|
т.е. эти события являются одновременными и пространственно совпадающими для любой инерциальной системы отсчёта.
Если события |
|
в системе |
К |
|
пространственно разобщены |
x1 x2 , но |
||||||||||||||||||||||
одновременны (t1=t2), то в системе К' согласно преобразованиям Лоренца: |
||||||||||||||||||||||||||||
x |
|
x1 Vt |
|
, |
|
x |
|
x |
2 Vt |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
|
1 |
2 |
|
|
|
|
2 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, т.е. x |
x |
и t t . |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
t |
Vx1 / c |
2 |
|
|
|
|
|
t |
Vx2 / c |
2 |
1 |
2 |
1 |
2 |
||||||||||||
t |
|
|
, |
t |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
|
|
|
1 |
2 |
|
|
|
|
2 |
|
|
|
1 |
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т.е. в системе К' эти события являются пространственно разобщёнными и неодновременными.
Следовательно, в одних системах отсчёта первое событие может предшествовать второму, в других системах отсчёта, наоборот, второе событие может предшествовать первому. Сказанное, однако, не относится к причинноследственным событиям, в которых порядок следования причинно-следственных событий одинаков во всех инерциальных системах отсчёта.
2. Длительность событий в различных системах отсчёта
Пусть в некоторой точке (с координатой x), покоящейся относительно системы К, происходит событие, длительность которого (разность показаний часов в начале и конце события) t2 t1 , где t1 – начало события, а t2 – конец события.
В системе К' длительность этого же события:
t t .
2 1
Согласно преобразованиям Лоренца начало и конец события:
|
|
|
|
t |
t Vx / c2 |
|
|
t |
|
t |
2 |
Vx / c2 |
|||||||||||
|
|
|
|
1 |
|
|
|
, |
|
|
|
|
|
|
|
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
1 |
2 |
|
|
2 |
|
|
|
1 2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда: |
|
t2 t1 |
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 2 |
|
|
|
1 2 |
|||||||||||||||||||
39

Отсюда вытекает, что , т.е. длительность события, происходящего в некоторой точке, наименьшая в той ИСО, относительно которой эта точка неподвижна. Или часы, движущиеся относительно ИСО, идут медленнее покоящихся часов.
3. Длина тел в различных системах отсчёта. |
|
|
|
|
|
|
Рассмотрим стержень, расположенный вдоль оси |
|
x |
и |
покоящийся |
относительно системы К'. Длина стержня в системе К' будет: l |
0 |
x |
x |
, |
|
|
|
2 |
1 |
|
|
где x |
, x – не изменяющиеся со временем t' координаты начала и конца стержня, а |
||||
1 |
2 |
|
|
|
|
индекс 0 показывает, что в системе К' стержень покоится.
Теперь определим длину этого стержня в системе К, относительно которой он движется, со скоростью V . Для этого измерим координаты концов стержня x1 и x2
системе К в один и тот же момент времени t. Их разность l x2 x1 и определяет длину стержня в системе К. Используя преобразования Лоренца, получим:
|
|
|
|
|
|
|
x2 |
Vt |
|
|
x1 |
Vt |
|
|
x2 |
x1 |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|||
l |
|
x |
x |
|
|
|
|
|
|
|
|
|
или |
l l |
|
1 |
2 |
|
. |
|||||||||||||
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||||||||||||
|
|
1 |
|
1 |
2 |
|
|
1 2 |
|
|
1 2 |
|
|
1 2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Таким образом, длина стержня, измеренная в системе, относительно которой он движется, оказывается меньше длины, измеренной в системе отсчёта, относительно которой стержень покоится.
Линейный размер тела, движущегося относительно инерциальной системы отсчёта, уменьшается в направлении движения в 
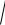 1 2 раз, т.е. так называемое лоренцево сокращение длины тем больше, чем больше скорость движения.
1 2 раз, т.е. так называемое лоренцево сокращение длины тем больше, чем больше скорость движения.
|
Из |
|
преобразований Лоренца для других координат: y |
y |
y |
2 |
y ; |
|
|
|
|
|
2 |
1 |
|
1 |
|
z |
z |
z |
2 |
z , т.е. поперечные размеры тела не зависят от скорости его движения и |
||||
2 |
1 |
|
1 |
|
|
|
|
|
одинаковы во всех инерциальных системах отсчёта.
Таким образом, линейные размеры тела наибольшие в той инерциальной системе отсчёта, относительно которой тело покоится.
4. Релятивистский закон сложения скоростей
Рассмотрим движение материальной точки в системе К, которая, в свою очередь, движется относительно системы К. Найдем величину скорости в системе К.
|
|
|
|
|
|
x |
Vt |
|
|
|
|
t Vx / c2 |
||||||||
Из преобразований Лоренца: |
x |
|
|
|
|
; y y ; |
z z ; t |
|
|
|
|
|
. |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
1 |
2 |
|
|
|
|
1 |
2 |
|||||||
Продифференцируем все уравнения: |
|
|
|
|
|
|
|
|
|
|
||||||||||
dx |
dx Vdt |
; dy dy ; dz dz ; dt |
dt Vdx / c2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 2 |
|
|
1 |
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
40
