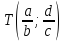- •Уравнения, разрешенные относительно производной. Задача Коши. Теорема о существовании и единственности решения.
- •Линейные уравнения 1-го порядка
- •Структура общего решения линейного уравнения
- •Фундаментальная система решений и общее решение однородного уравнения
- •Частные решения неоднородной системы
- •10. Фазовое пространство и фазовые траектории автономной системы. Свойства решений и фазовых траекторий.
- •11. Исследование положений равновесия и фазовые портреты линейных автономных систем на плоскости – случаи узла, седла, фокуса и центра.
- •12) Исследование положения равновесия нелинейной системы по линейному приближению (сорри что много, по другому никак)
- •13) Устойчивость положения равновесия автономной системы
- •14) Структура общего решения линейного разностного уравнения
- •15) Общее решение однородного и частное решение неоднородного уравнений
- •16. Модели с непрерывным временем
- •17. Модели с дискретным временем (стр. 119 – 120)
14) Структура общего решения линейного разностного уравнения
Рассмотрим уравнения вида:
![]() f(x),
где a0,а1,
а2
=
const
– коэф уравнения, f(x)
– его правая часть.
f(x),
где a0,а1,
а2
=
const
– коэф уравнения, f(x)
– его правая часть.
Определяем тип уравнения:
Когда f(x)=0, уравнение считают ОДНОРОДНЫМ;
Когда f(x) отлично от нуля, уравнение называют НЕОДНОРОДНЫМ.
Составляем характеристическое уравнение
Независимо от типа, решаем однородное уравнение
Если это неоднородное уравнение, то продолжаем решать его подставляя корни однородного в правую часть вида: F(n)=B*a^n, где B-искомый коэф., a=const, n-корень неоднородного уравнения
Структура общего решения уравнения имеет вид:

15) Общее решение однородного и частное решение неоднородного уравнений

Частное неоднородных:



16. Модели с непрерывным временем
В качестве независимой переменной выбрано время t.
Модель естественного роста (с. 17 – 20 в «Курсе лекций»)
Пусть y(t) – интенсивность выпуска продукции некоторого предприятия. Предположим, что имеет место аксиома о ненасыщаемости рынка (весь товар продан, цена p фиксирована).
Изменение скорости выпуска продукции зависит от инвестиций. Эта зависимость выражается прямой пропорциональностью, т.е. имеет место принцип акселерации:
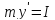 ,
(m=const),
m
– норма
акселерации.
,
(m=const),
m
– норма
акселерации.
Для увеличения интенсивности выпуска y(t), необходимо, чтобы чистые инвестиции (общ. объём инвестиций минус амортизационные затраты) были больше нуля.
Пусть
 – норма чистых инвестиций, т.е. часть
доходовpy,
которая тратится на чистые инвестиции,
тогда
– норма чистых инвестиций, т.е. часть
доходовpy,
которая тратится на чистые инвестиции,
тогда
 .
Подставляем
выражение в
.
Подставляем
выражение в
 .
.
 ,
или
,
или
 ,
где
,
где
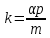 .
.
 называется
уравнением естественного роста.
называется
уравнением естественного роста.
Уравнение естественного роста представляет собой дифференциальное уравнение первого порядка с разделяющимися переменными.
 .
.
 .
.
 .
.
 .
.
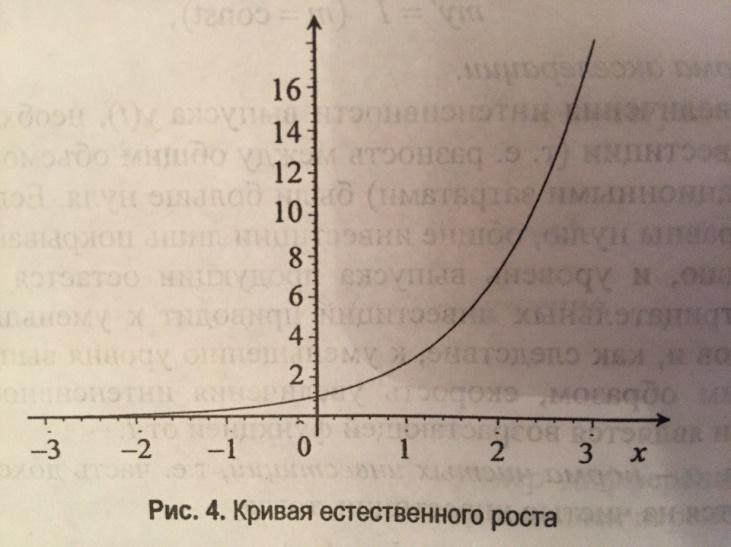
Интегральная
кривая уравнения
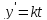 .
.
Если
 ,
то из
,
то из следует, что
следует, что ,
т.е.
,
т.е.
 .
.
Эту модель целесообразно применять для исследования начальных этапов развития экономической системы, так как с течением времени y может принимать как угодно большие значения, что не может не изменить цену.
Пример задачи: для обеспечения пищей одного человека нужна площадь 0,1 га. Всего на Земле 4000 млн. га. Если не использовать новые источники пищи, население не должно превышать 40000 млн. человек. Оно растёт со скоростью 1,8% в год. Когда будет достигнут предел насыщения?
Решение:
k=0,18,
1999 год – начальный момент времени (t=0),
когда население составило
 человек.
человек.

Требуется
найти
 ,
,
тогда

Логарифмируя,
получим
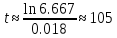 лет. Таким образом, согласно модели
Мальтуса, к 2104 г. при постоянном приросте
населения мир достигнет предела
насыщения.
лет. Таким образом, согласно модели
Мальтуса, к 2104 г. при постоянном приросте
населения мир достигнет предела
насыщения.
Модель логистического роста (с. 20 - 25)
Первым на несовершенство модели естественного роста обратил внимание П.Ф. Ферхюльст. Он пришёл к необходимости рассматривать переменный коэффициент роста. В результате этого процесс становился нелинейным, что изменяло его поведение.
 ,
здесь
,
здесь
 .
Уравнение
.
Уравнение представляет собой автономное
дифференциальное уравнение. Функция
возрастающая.
представляет собой автономное
дифференциальное уравнение. Функция
возрастающая.
Рассмотрим конкретный вид зависимости цены от выпуска:
 .
.

Проинтегрировав
уравнение
 получаем
получаем .
Интегральная кривая уравнения
.
Интегральная кривая уравнения называется логистической кривой. Анализ
логистической кривой показывает, что
при малыхt
логистический рост схож с естественным
ростом, однако при больших t
характер роста меняется, темпы роста
замедляются и кривая асимптотически
приближается к прямой
называется логистической кривой. Анализ
логистической кривой показывает, что
при малыхt
логистический рост схож с естественным
ростом, однако при больших t
характер роста меняется, темпы роста
замедляются и кривая асимптотически
приближается к прямой
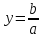 .
Это прямая является стационарным
решением уравнения
.
Это прямая является стационарным
решением уравнения и соответствует случаю
и соответствует случаю .
.
Многие
процессы можно описать уравнением
 ,
где
,
где
 .
Интегральная кривая такого дифференциального
уравнения называется обобщённой
логистической кривой. Используется это
уравнение для описания модели роста в
макроэкономики.
.
Интегральная кривая такого дифференциального
уравнения называется обобщённой
логистической кривой. Используется это
уравнение для описания модели роста в
макроэкономики.
Рассмотрим модель, в которой скорость роста зависит не от дохода, а от прибыли.
 –
функция
издержек, где
–
функция
издержек, где
 – переменные
издержки,
– переменные
издержки,
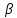 – постоянные, тогда
– постоянные, тогда

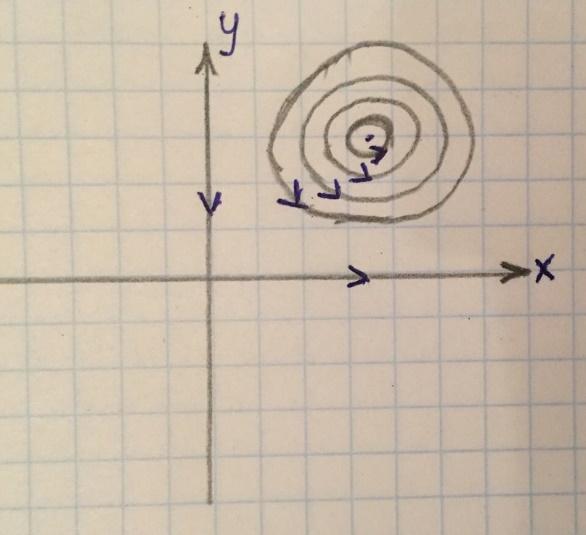
Модель Лотки-Вольтерры
Модель взаимодействия двух видов типа «хищник — жертва», названная в честь её авторов (Лотка; Вольтерра), которые предложили модельные уравнения независимо друг от друга. Математическая модель относится к типу чёрный ящик.
Такие уравнения можно использовать для моделирования систем «хищник — жертва», «паразит — хозяин», конкуренции и других видов взаимодействия между двумя видами.
Простым языком: сначала число жертв уменьшается до минимума, т.к. хищники их едят, потом есть становится нечего и число хищников уменьшается. Далее жертвы вновь размножаются, т.к. хищников мало. Затем, т.к. жертв опять много, их снова едят. И так по кругу.
В математической форме предложенная система имеет следующий вид:

 –численность
«жертв»
–численность
«жертв»
 –численность
«хищников»
–численность
«хищников»

Фазовый
портрет: