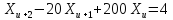1) ОДУ 1-го порядка:

с разделяющимися переменными

Линейные

задача Коши

2) Линейные ОДУ с постоянными коэффициентами

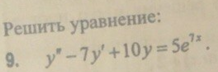
3) Системы линейных ОДУ с постоянными коэффициентами –

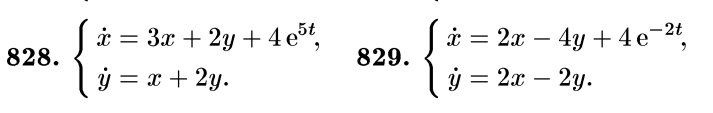
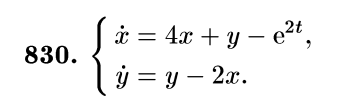
4) Исследование положений равновесия и фазовые портреты линейных автономных систем на

Плоскости

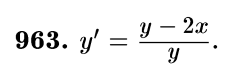
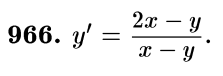
5) Разностные уравнения

1)

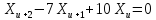
2)

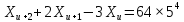
3)

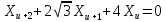
4)

1. 

2. 

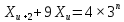
1. Уравнения, разрешенные относительно производной. Задача Коши. Теорема о существовании и единственности решения.

1. Обыкновенным дифференциальным уравнением F(x,y,y’,…, y^n)=0, где х принадлежит R, у(х) – искомая функция, у’,…, y^n – производные.

Решением уравнения называется функция f(x), имеющая производную доn-ого порядка, подстановка которой в искомое уравнение обращает его в тождество.

Уравнение y^n=f(x,y,y’, …,y^(n-1)) называется разрешенным относительно старшей производной.

2. Задача Коши: отыскание решение уравнения y’=f(x,y), удовлетворяющего начальному условиюy(x0) =y0.

3. Теорема о существовании и единственности решения.

Если в некоторой окрестности точки (х0, у0) функция f (x, y) определена, непрерывна и имеет непрерывную частную производную f ’ y, то существует такая окрестность точки (х0, у0), в которой задача Коши y’=f (x, y), y(x0)=y0 имеет решение, притом только одно.

2. Уравнения с разделяющимися переменными: y’=f(x)g(x), g(х) и f(х) - заданные функции.

Все постоянные решения находятся из уравнения g(x)=0. Любому корню y0 отвечает решение у=у0.

Если у(х) не равно 0, dy:dx=f(x)g(x) => dy:g(x)=f(x)dx.

Интегрируем,то есть находим соответствующие первообразные G(у) и F(x), получаем множетство решений,заданное в неявной форме: G(x)=F(x)+C, где С-произвольная константа.

Выразив у, получим явное представление.

3. Линейные уравнения 1-го порядка

Определение линейного уравнения первого порядка

Дифференциальное уравнение вида

y′+a(x)y=f(x),

где a(x) и f(x) − непрерывные функции x, называтся линейным неоднородным дифференциальным уравнением первого порядка. Мы рассмотрим два метода решения указанных уравнений:

• Использование интегрирующего множителя;

• Метод вариации постоянной.

Использование интегрирующего множителя

Если линейное дифференциальное уравнение записано в стандартной форме:

y′+a(x)y=f(x),

то интегрирующий множитель определяется формулой:

u(x)=exp(∫a(x)dx).

Умножение левой части уравнения на интегрирующий множитель u(x) преобразует ее в производную произведения y(x)u(x).  Общее решение дифференциального уравнения выражается в виде:

y=∫u(x)f(x)dx+Cu(x),

где C − произвольная постоянная.

Метод вариации постоянной

Данный метод аналогичен предыдущему подходу. Сначала необходимо найти общее решение однородного уравнения:

y′+a(x)y=0.

Общее решение однородного уравнения содержит постоянную интегрирования C. Далее мы заменяем константу C на некоторую (пока еще неизвестную) функцию C(x). Подставляя это решение в неоднородное дифференциальное уравнение, можно определить функцию C(x).  Описанный алгоритм называется методом вариации постоянной. Разумеется, оба метода приводят к одинаковому результату.

4. Структура общего решения линейного уравнения

Рассмотрим уравнения вида:

y’’+a₁y’+a₂y=f(x), где а₁, а₂ = const – коэф уравнения, f(x) – его правая часть.

• Когда f(x)=0, уравнение считают ОДНОРОДНЫМ;

• Когда f(x) отлично от нуля, уравнение называют НЕОДНОРОДНЫМ.

Структура общего решения уравнения y’’+a₁y’+a₂y=f(x) имеет вид:

y=y₀+y^, где y₀ – общее решение однородного уравнения, y^ - произвольное частное решение уравнения.

5. Фундаментальная система решений и общее решение однородного уравнения

Построим общее решение уравнения y’’+a₁y’+a₂y=0

Если y₁(x), y₂(x) – какие-либо частные решения уравнения, то любая их линейная комбинация:

y=C­₁y₁+C₂y₂ с производными постоянными С также является решением.

Если С₁, С₂ линейно независимы, то есть не получаются одно из другого при умножении на коэффициент, то y=C­₁y₁+C₂y₂ дает общее решение уравнения y’’+a₁y’+a₂y=0.

Фундаментальная система решений (ФСР): построение общего решения уравнения y’’+a₁y’+a₂y=0 сводится к отысканию пары линейно независимых решений у₁(х), у₂(х).

Решение в два этапа:

1. Составляем характеристическое уравнение Л²+а₁Л+а₂ относительно неизвестной Л, где каждая производная заменяется соответствующей степенью Л. Находим корни Л₁ и Л₂.

2. Три варианта решения, в зависимости от найденных Л:

1. Действительные и различные (Л₁ не= Л₂)

у₁=е^Л₁^х, у₂=е^л₂^х;

2. Действительные и совпадают (Л₁=Л₂=а)

у1=е^ах, у2=х*е^ах;

3. Комплексные Л₁=A+Bi; Л₂=A-Bi,

то у1=e^ax*cosBx, y2=e^ax*sinBx.

6. Способы построения частного решения неоднородного уравнения.

f(x)=k*e^(ux)

Где k и u - постоянные, ограничимся случаем, когда u не является корнем характер. уравнения.

Частное решения уравнения следует искать в виде y=A*e^(ux), где А - постоянная, определяемая после подстановки выражения y=A*e^(ux) в y"+ay'+ay=f(x)

7. Структура общего решения линейной системы. +8. Представление общего решения однородной системы.

Однородной системой m линейных уравнений с n неизвестными называется система вида

a11x1 + a12x2 + … + a1nxn = 0 a21x1 + a22x2 + … + a2nxn = 0 … … … … … … … … … … … am1x1 + am2x2 + … + amnxn = 0

Эта система может быть записана в виде матричного уравнения

A · X = O.

Система (1) всегда совместна, так как:

1. имеет очевидное решение x₁⁰  =  x₂⁰  =   …   =  x_n⁰ = 0 , которое называется нулевым, или тривиальным;

2. добавление нулевого столбца не меняет ранга матрицы, следовательно, выполняется достаточное условие теоремы Кронекера–Капелли.( Для того чтобы линейная система являлась совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу её основной матрицы.)

Естественно, нас интересуют нетривиальные решения однородной системы.

Условие нетривиальной совместности:

Для того, чтобы однородная система имела нетривиальное решение, необходимо и достаточно, чтобы ранг ее основной матрицы был меньше числа неизвестных.

Следствие. Для того, чтобы однородная система n линейных уравнений с n неизвестными (матрица системы A — квадратная) имела нетривиальное решение, необходимо и достаточно, чтобы определитель матрицы этой системы был равен нулю ( det  A = 0 ).

Общим решением системы линейных уравнений называется формула, которая определяет любое ее решение.

Фундаментальной системой решений однородной системы (1) называется n − r линейно независимых решений этой системы.

Cтолбцы фундаментальной системы решений обозначаются X₁,  X₂,   … ,  X_n − r .

Теорема о структуре общего решения однородной системы уравнений:

Любое решение однородной системы линейных уравнений определяется формулой

X = C1 · X1 + C2 · X2 + … + Cn − r · Xn − r,

(2)

где X₁,  X₂,   … ,  X_n − r — фундаментальная система решений однородной системы линейных уравнений и C₁,  C₂,   … ,  C_n − r — произвольные постоянные.

Свойства общего решения однородной системы уравнений:

1. При любых значениях C₁,  C₂,   … ,  C_n − r    X , определяемое формулой (2), является решением системы (1).

2. Каково бы ни было решение X₀ , существуют числа C₁⁰,   … ,  C_n − r⁰ такие, что

X0 = C10 · X1 + C20 · X2 + … + Cn − r0 · Xn − r.

Пример Метод Гаусса

Решить однородную систему линейных уравнений

Решение: запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду. Первое действие направлено не только на получение единичного значения, но и на уменьшение чисел в первом столбце:

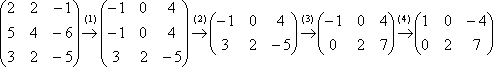
(1) К первой строке прибавили третью строку, умноженную на –1. Ко второй строке прибавили третью строку, умноженную на –2. Слева вверху я получил единицу с «минусом», что зачастую намного удобнее для дальнейших преобразований.

(2) Первые две строки одинаковы, одну из них удалили. Честное слово, не подгонял решение – так получилось. Если выполнять преобразования шаблонно, то линейная зависимость строк обнаружилась бы чуть позже.

(3) К третьей строке прибавили вторую строку, умноженную на 3.

(4) У первой строки сменили знак.

В результате элементарных преобразований получена эквивалентная система:

Алгоритм работает точно так же, как и для неоднородных систем. Переменные , «сидящие на ступеньках» – главные, переменная , которой не досталось «ступеньки» – свободная.

Выразим базисные переменные через свободную переменную:

Ответ: общее решение:

Пример Метод собственных значений