
Bezverkhniy_Kratnye_integraly_2014
.pdf
8. ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНОМ ИНТЕГРАЛЕ
8.1. Переход к цилиндрическим координатам
При вычислении тройных интегралов иногда бывает полезно выполнить замену переменных. В этом пункте рассмотрим переход к цилиндрическим координатам, а в следующем — к сфериче-
ским. |
|
|
Пусть новые переменные ρ, ϕ, z связаны со старыми |
x, y, z |
|
соотношениями |
|
|
x |
= ρcosϕ, |
|
|
= ρsin ϕ, |
|
y |
(8.1) |
|
|
= z, |
|
z |
|
|
где 0 ≤ ϕ ≤ 2π, 0 ≤ ρ < +∞, −∞ < z < +∞.
Переход в тройном интеграле от прямоугольных координат ( x, y, z) к цилиндрическим (ρ, ϕ, z) осуществляется по формуле
|
∫∫∫ f (x, y, z)dxdydz = ∫∫∫ f (ρcos ϕ,ρsin ϕ, z)ρdϕdρdz, |
(8.2) |
||||
|
V |
|
|
V ′ |
|
|
где V ′ |
— область изменения цилиндрических координат, соответ- |
|||||
ствующая объему V. |
|
|
|
|||
Пример 8.1. Вычислить тройной интеграл |
|
|
||||
|
∫∫∫( x2 + y2 )dxdydz, |
|
|
|||
|
V |
|
|
|
|
|
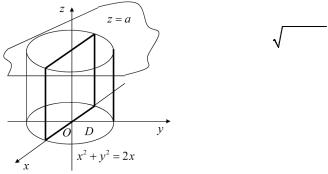
если область V ограничена плос- |
|
|
||||
костью |
z = 2 и |
параболоидом |
|
|
||
x2 + y2 = 2z |
(рис. 8.1). |
|
|
|
||
Решение. Область V |
ограни- |
|
|
|||
чена снизу параболоидом, а сверху |
|
|
||||
плоскостью |
z = 2. |
Область V |
|
|
||
проектируется в область |
D плос- |
|
|
|||
кости xOy, |
ограниченную окруж- |
Рис. 8.1 |
|
|||
51
ностью |
x2 + y2 = 4. |
Последнее уравнение получено в результате |
|||||||||||||||||||||||||||
исключения z |
из |
уравнений |
плоскости |
z = 2 |
и параболоида |
||||||||||||||||||||||||
2z = x2 + y2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Перейдем |
к |
цилиндрическим |
|
|
|
координатам. |
Так |
как |
|||||||||||||||||||||
x2 + y2 = ρ2 cos2ϕ + ρ2 sin 2ϕ = ρ2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
∫∫∫(x2 + y2 )dxdydz = ∫∫∫ρ2ρdϕdρdz. |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
V |
|
|
|
|
|
|
|
V ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В области V координата ϕ изменяется от 0 до 2π, |
ρ — от 0 |
||||||||||||||||||||||||||||
до 2, z |
— от параболоида ρ2 / 2 до плоскости z = 2. Итак, |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
∫∫∫(x2 + y2 )dxdydz = ∫∫∫ρ2ρdρdϕdz = ∫ dϕ∫ρ3dρ ∫ dz = |
|
|
|
|
|
|
|||||||||||||||||||||||
V |
|
|
|
|
|
V ′ |
|
|
|
|
|
|
0 |
|
|
0 |
|
ρ2 /2 |
|
|
|
|
|
|
|
|
|||
2π |
2 |
2 |
|
2 |
|
2π |
2 3 |
|
|
ρ2 |
|
|
|
|
2π |
2 |
|
|
3 |
− |
ρ5 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
= ∫ dϕ ∫ρ |
|
z |
|
dρ = ∫ dϕ∫ρ |
2 − |
|
|
dρ = |
∫ dϕ∫ |
2ρ |
|
|
dρ = |
||||||||||||||||
0 |
0 |
|
|
ρ2 /2 |
0 |
0 |
|
|
|
2 |
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
2π |
ρ4 |
|
|
ρ6 |
|
|
8 |
2π |
|
|
8 |
|
2π |
16π |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
= ∫ |
|
− |
|
|
|
|
dϕ |
= |
|
∫ dϕ = |
|
|
ϕ |
= |
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
0 |
2 |
|
|
12 |
|
|
0 |
|
3 |
0 |
|
|
|
3 |
|
0 |
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Пример 8.2. Вычислить трой- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
ной интеграл |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫∫z |
x2 + y2 dxdydz, |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
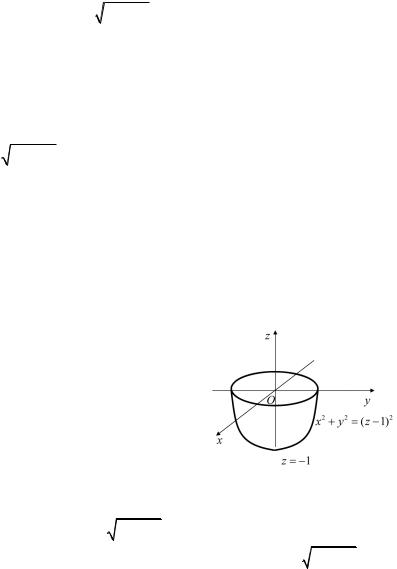
если область V ограничена плоско- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
стями |
|
y = 0, |
z = 0, |
z = a и цилин- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
дром x2 + y2 = 2x (рис. 8.2). |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Область V ограничена |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
снизу плоскостью z = 0, а сверху — |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
плоскостью |
z = a. |
Она проектиру- |
||||||||||||||||||
|
|
Рис. 8.2 |
|
|
|
ется в область |
D плоскости |
xOy, |
|||||||||||||||||||||
52
ограниченную отрезком [0; 2] оси Ox и полуокружностью
x2 + y2 = 2x.
Перейдем к цилиндрическим координатам:
|
|
|
|
|
∫∫∫z |
|
|
x2 + y2 dxdydz = ∫∫∫zρ2dϕdρdz. |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V ′ |
|
|
|
|
|
|
|
|
|
|
|
|
Очевидно, что в области V |
координата ϕ меняется от |
0 до |
|||||||||||||||||||||||||||||
π / 2; |
ρ — от 0 |
до ρcos ϕ (в полярных координатах уравнение |
||||||||||||||||||||||||||||||
окружности |
x |
2 + y2 = 2x |
имеет вид ρ2 = 2ρcosϕ, |
т. е. ρ = 2cosϕ ), |
||||||||||||||||||||||||||||
z меняется от 0 до a. Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π/2 2cosϕ2cosϕ |
|
a |
|
|
|
|
|||||
∫∫∫z |
x2 + y2 dxdydz = ∫∫∫ρ2 zdρdϕdz = ∫ d |
∫ |
|
∫ |
ρ2dρ∫zdz = |
|
|
|||||||||||||||||||||||||
V |
|
|
|
|
|
|
|
V ′ |
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
0 |
|
|
|
|
||||
|
|
π/2 |
2cosϕ |
z |
2 |
|
a |
|
a |
2 π/2 |
3 |
|
|
2cosϕ |
|
|
4a |
2 π/2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
= ∫ dϕ |
∫ |
ρ2 |
|
|
dρ= |
|
|
∫ |
ρ |
|
|
|
dϕ = |
|
|
∫ cos3ϕdϕ = |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
0 |
|
0 |
|
2 |
|
0 |
2 |
|
0 |
3 |
|
|
0 |
|
|
3 |
|
|
0 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π/2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
4a2 |
π |
|
|
2 |
|
|
|
|
|
|
4a2 |
|
|
|
sin3ϕ |
|
|
4a2 |
1 |
8a2 |
|||||||||||
= |
|
∫2(1− sin ϕ)d(sin ϕ) = |
|
|
|
|
sin ϕ |
|
|
= |
|
|
1− |
|
= |
|
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
3 |
0 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
0 |
|
|
3 |
3 |
9 |
|
||||||
|
Пример 8.3. Вычислить тройной интеграл |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
∫∫∫(( x + y)2 − z)dxdydz, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если |
область |
T |
ограничена |
по- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
верхностями |
|
z = 0 |
и |
(z −1)2 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= x2 + y2 |
(рис. 8.3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Решение. |
|
Область |
T пред- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ставляет собой конус. Уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
конической поверхности, ограни- |
|
|
|
|
|
|
|
|
Рис. 8.3 |
|
|
|
|
|||||||||||||||||||
чивающей область T , можно за- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
писать в виде |
z = 1 − |
x2 + y2 , |
|
а саму область T |
|
представить сле- |
||||||||||||||||||||||||||
дующим образом: T = {(x, y, z) : (x, y) σ,0 ≤ z ≤ 1 − x2 + y2 }, где
53
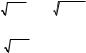
σ — круг радиуса 1 с центром в начале координат. Поэтому данный тройной интеграл можно свести к последовательному вычислению трех определенных интегралов в прямоугольных координатах:
1 |
1−x2 |
1− x2 + y2 |
I = ∫ dx |
∫ dy |
∫ ((x + y)2 − z)dz. |
−1 |
− 1−x2 |
0 |
Однако удобнее перейти к цилиндрическим координатам (ρ, ϕ, z) : x = ρcosϕ, y = ρsin ϕ, z = z. Тогда прообраз круга σ есть прямоугольник {(ρ,ϕ) : 0 ≤ ρ ≤ 1, 0 ≤ ϕ ≤ 2π}, прообраз конической поверхности — плоская поверхность z = 1 − ρ, а прообраз области
σ — область τ в пространстве с координатными осями Oρ, Oϕ, Oz, представляющая собой треугольную призму с основаниями, параллельными плоскости ρOz.
Якобиан перехода к цилиндрическим координатам равен ρ, подынтегральная функция в цилиндрических координатах равна
ρ2 (1 + sin 2ϕ) − z. Сводя тройной интеграл по области τ к последовательному вычислению трех определенных интегралов, получим
2π 1 1−ρ
I = ∫∫∫[ρ2 (1 + sin 2ϕ) − z]ρdρdϕdz = ∫ dϕ∫dρ ∫ [ρ2 (1 + sin 2ϕ) − z]ρdz =
τ |
|
|
|
0 0 |
|
0 |
|
|
2π |
1 |
|
3 |
|
1 |
|
2 |
|
= ∫ dϕ∫ ρ |
|
(1 − ρ)(1 + sin 2ϕ) − |
|
ρ(1 − ρ) |
|
dρ = |
||
|
|
|
||||||
0 |
0 |
|
|
|
2 |
|
|
|
2π |
1 |
|
|
1 |
|
π |
|
= ∫ |
|
(1 |
+ sin 2ϕ) − |
|
dϕ = |
|
. |
|
|
|
|||||
0 |
20 |
|
|
24 |
|
60 |
|
Расстановку пределов интегрирования в цилиндрических координатах можно провести, ограничившись рассмотрением изменения цилиндрических координат в области T и не рассматривая область τ.
Задача 8.1. Перейти к цилиндрическим координатам и вычислить интегралы:
54

а) |
∫∫∫ |
|
x2 + y2 zdxdydz, |
где T — область, ограниченная по- |
||||
|
T |
|
|
|
|
|
|
|
верхностями x |
2 + y |
2 = z, z = 1; |
||||||
|
3 |
|
|
|
|
|
2 |
|
|
|
z |
|
z− y |
|
|||
б) ∫zdz ∫ y2dy |
∫ |
x2dx; |
||||||
|
0 |
− |
z |
|
|
|
2 |
|
|
|
|
− |
z |
− |
y |
|
|
|
|
|
|
|
|
|
||
в) |
∫∫∫xydxdydz, |
где T |
— область, ограниченная поверхностя- |
|||||
|
T |
|
|
|
|
|
|
|
ми x2 + y2 = 1, z = 0, z = 1, x ≥ 0, y ≥ 0.
8.2.Переход к сферическим координатам
Вэтом пункте мы рассмотрим переход от прямоугольных координат ( x, y, z) к сферическим координатам (ϕ, θ, ϕr) в тройном
интеграле. Они связаны соотношениями
x = r cosϕsin θ;
y = r sin ϕsin θ;
θz = r cos ,
где 0 ≤ ϕ ≤ 2π, 0 ≤ θ ≤ π, 0 ≤ r < +∞.
Формула перехода в тройном интеграле к сферическим координатам имеет вид
∫∫∫ f (x, y, z)dxdydz =
V
= ∫∫∫ f (r cos ϕsin θ, r sin ϕsin θ, r cos θ)r 2 sin θd ϕd θdr,
V′
где V ′ — область изменения сферических координат, соответствующая объему V.
Пример 8.4. Вычислить тройной интеграл
∫∫∫ x2 + y2 + z2 dxdydz,
V
55

если область V ограничена сферой x2 + y2 + z2 = z.
Решение. В сферических координатах уравнение сферы, огра-
ничивающей область V , имеет вид: r2 = r cosθ, |
или r = cosθ, так |
||
как x2 + y2 + z2 = r2. Поэтому |
|
|
|
∫∫∫ |
x2 + y2 + z2 dxdydz = ∫∫∫rr2 sin θdrϕdθ. |
|
|
V |
V ′ |
|
|
Очевидно, что в области V угол ϕ изменяется от 0 до 2π, θ — |
|||
от 0 до π / 2, r |
— от 0 до cosθ. Тогда |
|
|
|
2π |
π/2 |
cosθ |
∫∫∫ x2 + y2 + z2 dxdydz = ∫∫∫r3 sin θdϕdθdr = ∫ dϕ ∫ sin θdθ ∫ r3dr =
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
V ′ |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
0 |
|
|
|
|
||||
|
|
|
|
|
|
2π |
|
|
π/2 |
|
|
r |
4 |
|
cosθ |
|
|
1 |
2π |
π/2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
= ∫ dϕ ∫ sin θ |
|
|
|
|
|
|
dθ = |
∫ dϕ ∫ sin θcos4 θdθ = |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
0 |
|
4 |
|
0 |
|
|
|
4 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
2π |
|
|
π/2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
1 |
2π cos5θ |
|
π/2 |
|
|
1 |
|
2π |
1 |
|
2π |
|
π |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
= − |
|
|
∫ dϕ ∫ cos |
|
θd(cosθ) = − |
|
∫ |
|
|
|
|
|
|
|
dϕ = |
|
|
|
∫ dϕ = |
|
ϕ |
|
= |
|
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
4 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
0 |
5 |
|
|
|
0 |
|
|
20 |
|
0 |
20 |
|
0 |
10 |
|
|||||||||
Задача 8.2. Перейти к сферическим координатам и вычислить |
||||||||||||||||||||||||||||||||||||||||||
интегралы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
а) ∫∫∫ x2 + y2 + z2 dxdydz, |
где T |
— область, ограниченная по- |
||||||||||||||||||||||||||||||||||||||||
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
верхностью x |
2 + y2 + z |
2 = x; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
9−x |
|
|
|
18−x |
− y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
б) |
∫ x2dx |
∫ |
|
|
y2dy |
|
|
∫ |
|
|
|
zdz; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
3 |
|
|
9−x |
2 |
|
|
2 |
+ y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
− |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
в) ∫∫∫ |
|
z ln(x2 + y2 + z2 +1)dxdydz |
|
|
|
2 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; x |
|
+ y |
|
+ z |
|
|
= 1; |
|
|
|
|
|
|
||||||||||
|
|
|
x |
2 |
+ y |
2 |
+ z |
2 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
г) |
|
|
∫∫∫xyzdxdydz, x2 + y2 + z2 = R2 ; x2 + y2 + z2 |
= 2Rz |
|
(общая |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
часть); |
x ≥ 0, y ≥ 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
56
9.ВЫЧИСЛЕНИЕ ОБЪЕМОВ
СПОМОЩЬЮ ТРОЙНЫХ ИНТЕГРАЛОВ
Объем пространственного тела V вычисляется по формуле
V = ∫∫∫dxdydz.
V
В цилиндрических и сферических координатах имеем
|
V = ∫∫∫ρdρdϕdz, |
|
V ′ |
|
V = ∫∫∫r2 sin θdrdϕdθ. |
|
V ′ |
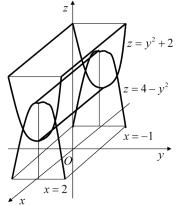
Пример 9.1. Вычислить объем |
|
тела, ограниченного |
цилиндрами |
z = 4 − y2 , z = y2 + 2 |
и плоскостя- |
ми x = −1, x = 2 (рис. 9.1). Решение. Рассматриваемое тело
ограничено |
сверху цилиндром |
z = 4 − y2 , |
а снизу — цилиндром |
z = y2. Нетрудно найти область D плоскости xOy, в которую проек-
тируется это |
тело: |
плоскости |
|
x = −1, |
x = 2 пересекаются с плос- |
||
костью |
xOy по прямым с такими |
||
|
|
|
Рис. 9.1 |
же уравнениями; |
для |
нахождения |
|
проекций прямых, по которым пересекаются цилиндры, исключаем из их уравнений z, т. е. приравниваем правые части этих урав-
нений: 4 − y2 = y2 + 2. Отсюда получаем: y = ±1. Таким образом, область D в плоскости xOy ограничена прямыми x = −1, x = 2, y = 1, y = −1.
С учетом симметрии области V относительно плоскости xOz имеем
57
2 |
1 |
4− y2 |
|
|
2 |
1 |
|
4− y2 |
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
V = 2∫ dx∫dy ∫ dz = 2 ∫dx ∫z |
|
|
dy = 2 ∫ dx∫(4 − y2 − y2 − 2)dy = |
|||||||||||||||||||||||||
−1 |
0 |
2 |
+2 |
|
|
|
−1 |
0 |
|
2 |
+2 |
|
|
−1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1 |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
y3 |
|
|
|
2 |
|
1 |
|
8 |
|
2 |
8 |
|
|
2 |
16 |
|
8 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
= 4 ∫ |
y |
− |
|
|
|
dx = 4 ∫ |
1 − |
|
dx |
= |
|
|
∫dx |
= |
|
|
x |
= |
|
+ |
|
= 8. |
||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
−1 |
|
|
3 |
|
|
|
|
|
−1 |
3 |
|
|
3 −1 |
3 |
|
−1 |
|
3 3 |
|||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
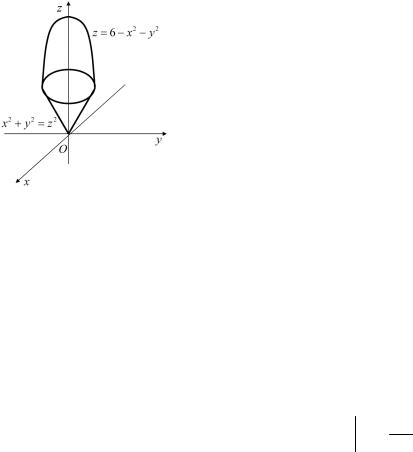
Пример 9.2. Вычислить объем тела, ограниченного параболо- |
||||||||||||||||||||||||||||
идом z = 6 − x |
2 − y |
2 и конусом z2 |
= x2 + y2 |
(z ≥ 0) |
(рис. 9.2). |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Рассматриваемое те- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ло ограничено снизу конусом, а |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
сверху — параболоидом и проек- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
тируется в область D плоскости |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
xOy, |
ограниченную окружностью |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x2 + y2 = 4. |
Последнее |
уравнение |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
получено в результате исключе- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ния |
z из уравнений конуса и па- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
раболоида: тем самым мы нахо- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
дим |
проекцию |
в |
плоскость |
|
xOy |
||||||||||||
линии пересечения этих двух поверхностей.
При вычислении тройного интеграла перейдем к цилиндрическим координатам. С учетом того что данное тело симметрично относительно плоскостей xOy, yOz
и что уравнения окружности, ограничивающей область D, конуса
и параболоида |
соответственно |
принимают |
вид ρ = 2, z = ρ, |
|||||
z = 6 − ρ2 , имеем |
|
|
|
|
|
|
||
π/2 |
2 |
2 |
π/2 |
2 |
|
6−ρ2 |
π/2 |
2 |
6−ρ |
|
|
||||||
V = ∫ dϕ∫ρdρ ∫ dz = 4 ∫ dϕ ∫ρz |
|
|
dρ = 4 ∫ dϕ∫(6ρ − ρ3 − ρ2 )dρ = |
|||||
0 |
0 |
ρ |
0 |
0 |
|
ρ |
0 |
0 |
|
|
|
|
|
|
|
|
|
π/2 |
|
2 |
|
ρ2 |
ρ3 |
|
2 |
64 |
π/2 |
64 |
|
|
|
||||||||||
= 4 ∫ |
3ρ |
|
− |
− |
|
|
|
dϕ = |
|
∫ dϕ = |
|
|
|
|
|
|
|||||||
0 |
|
|
|
4 |
3 |
|
|
0 |
3 |
0 |
3 |
π/2
0
= 32π . 3
58

Пример 9.3. Вычислить объем тела, ограниченного поверхностью (x2 + y2 + z2 )3 = 3xyz.
Решение. Левая часть уравнения поверхности, ограничивающей тело, положительна при любых значениях x, y, z, значит, тело расположено в тех октантах, где произведение xyz, стоящее в пра-
вой части уравнения поверхности, положительно, т. е. в I, III, VI, VIII октантах. Очевидно, что части тела, расположенные в этих октантах, одинаковы, поэтому вычисляем объем лишь той части, которая расположена в I октанте, а полученный результат умножаем на четыре.
Запишем в сферических координатах уравнение поверхности
|
|
r |
6 = 3r |
3 sin ϕcosϕsin2 θcosθ, |
|
|
|
||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
r = 3 3 3 sin ϕcosϕsin2 θcosθ. |
|
|
|
||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
π/2 |
π/2 |
3 3sinϕcosϕsin2 θcosθ |
π/2 |
π/2 |
|
r |
3 |
|
3 3sinϕcosϕsin2 θcosθ |
||
|
|
||||||||||
V = 4 ∫ dϕ ∫ sinθdθ |
∫ |
dθ = 4 ∫ 2φ ∫ |
sinθ |
|
|
= |
|||||
|
|
||||||||||
0 |
0 |
|
0 |
|
0 |
0 |
3 |
0 |
|||
π/2 |
|
π/2 |
|
π/2 |
|
|
|
π/2 |
|||
= 4 ∫ sin ϕ cosϕdϕ ∫ sin3θcosθdθ = 4 ∫ sin ϕd(sin ϕ) ∫ sin3θd(sin θ) =
0 |
|
0 |
0 |
|
0 |
|
|
|
|
|
|
|
π/2 |
|
π/2 |
π/2 |
|
sin 2ϕ |
|
π/2 |
1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
|
∫ |
4 |
|
∫ |
|
|
|
|
|||
= |
sin ϕ(sin θ) |
d(sin ϕ) = |
sin ϕd(sin ϕ) = |
2 |
|
|
= |
|
. |
||
|
|
|
|||||||||
|
0 |
|
0 |
0 |
|
|
0 |
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Задача 9.1. Перейти к сферическим координатам и вычислить объем тела, ограниченного поверхностями:
а) |
x2 + y2 + z2 = 1, x2 + y2 + z2 = 16, z2 = x2 + y2 , y = 0, z = 0, |
y = x |
(x ≥1, y ≥ 0, z ≥ 0); |
б) (x2 + y2 + z2 )2 = a2 (x2 + y2 − z2 ).
59
Задача 9.2. Найти объем тела, ограниченного сферой x2 + y2 +
+ z2 = 4 и параболоидом x2 + y2 = 3z (перейти к цилиндрическим координатам).
Задача 9.3. Перейдя к сферическим координатам, вычислить объемы тел, ограниченных данными поверхностями:
а) (x2 + y2 + z2 )2 = a3 x;
б) (x2 + y2 + z2 )2 = a2 (x2 + y2 ); в) (x2 + y2 + z2 )3 = a2 y2 z2 .
Задача 9.4. Найти объем тела, вырезанного в шаре радиуса b цилиндром радиуса a, ось которого проходит через центр шара.
10.ПРИЛОЖЕНИЕ ТРОЙНОГО ИНТЕГРАЛА
КЗАДАЧАМ МЕХАНИКИ
Пусть V — область пространства, занимаемая каким-нибудь материальным телом с плотностью μ(x, y, z). Тогда:
a) массу m этого тела вычисляют по формуле
m = ∫∫∫µ(x, y, z)dxdydz; |
(10.1) |
V |
|
б) моменты инерции I x , I y , I z относительно |
координатных |
осей Ox, Oy, Oz ; I xy , I xz , I yz относительно координатных плоскостей xOy, xOz, yOz, IO относительно начала координат соответственно находят по следующим формулам:
Ix = ∫∫∫( y2 + z2 )µ(x, y, z)dxdydz; |
I y |
= ∫∫∫( x2 + z2 )µ( x, y, z)dxdydz; |
V |
|
V |
Iz = ∫∫∫(x2 + y2 )µ(x, y, z)dxdydz; |
||
V |
|
|
Ixy = ∫∫∫z2µ(x, y, z)dxdydz; |
Ixz |
= ∫∫∫y2µ( x, y, z)dxdydz; (10.2) |
V |
|
V |
60
