
Bezverkhniy_Kratnye_integraly_2014
.pdf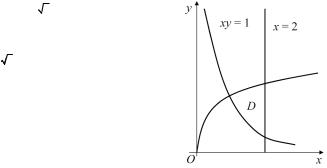
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
∫∫y ln xdxdy = ∫ ln xdx ∫ ydy = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
D |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1/ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
y2 |
|
|
|
|
x |
|
|
|
2 |
|
|
|
x |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
= ∫ ln xdx |
|
|
|
|
|
|
|
|
|
|
|
|
= |
∫ ln x |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
1 |
|
|
|
|
2 |
|
|
|
|
|
1/ x |
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
x2 |
|
1 2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
= |
|
|
|
|
|
|
ln xd |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
ln xd |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
∫1 |
|
|
|
|
|
|
|
2 |
|
|
2 ∫1 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.6 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x2 |
|
2 − |
|
|
|
2 |
x2 |
|
|
|
|
|
|
|
|
|
2 − |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
= |
1 |
ln x |
|
|
1 |
|
|
dx |
+ |
|
1 |
ln x |
1 |
|
1 |
1 |
|
dx |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
2 ∫ |
2 |
|
|
|
x |
|
|
|
|
2 |
|
|
|
|
|
|
|
x |
1 |
|
2 |
∫ x x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
|
|
|
1 2 |
|
x |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 2 |
dx |
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
2 |
|
|
|
ln 2 |
|
|
1 |
|
1 |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
= ln 2 − |
|
|
|
|
|
|
|
|
|
|
|
dx + |
|
|
|
ln 2 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
= ln 2 |
− |
|
|
|
|
|
|
|
|
x |
|
|
|
+ |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
= |
|
||||||||||||||||||||||||||
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
∫ x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
4 |
|
|
|
|
1 |
|
|
4 |
|
|
|
|
2 |
|
x |
|
1 |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
ln 2 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
3 |
|
|
ln 2 |
|
|
1 1 5ln 2 |
|
|
5 |
|
||||||||||||||||||||||||||||||||||||||
= ln 2 − |
|
|
|
|
|
− |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
= ln 2 − |
|
|
|
+ |
|
|
|
− |
|
|
|
|
= |
|
|
|
|
|
|
|
− |
|
|
. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 8 |
|
|
|
|
4 |
|
|
|
|
|
2 |
|
|
|
2 1 |
|
|
|
|
|
|
|
|
8 |
|
|
|
4 |
|
|
2 2 |
|
|
|
|
4 |
|
|
|
|
8 |
|
|||||||||||||||||||||||||||||||||||||
|
Пример 1.5. Вычислить двойной интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫xydxdy, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
область |
|
|
|
D |
|
ограничена |
|
параболой |
|
|
|
y = x2 |
|
и окружностью |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x2 + y2 = 2 и расположена ниже параболы.
Решение. Область D не является простой ни относительно оси Ox, ни относительно оси Oy, поэтому приходится разбивать ее на
три простые относительно оси Oy области: D1, D2 , D3 прямыми x = 1, x = −1, проходящими через точки пересечения параболы и окружности (рис. 1.7).
11
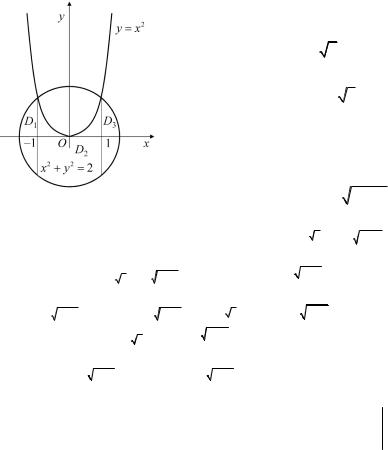
К каждой из этих областей приме-
нима формула (1.3). Область D1 |
проек- |
||||
тируется в отрезок [− 2; −1] оси Ox, |
|||||
область D2 — в отрезок [−1; 1], об- |
|||||
ласть D3 |
— в отрезок [1; |
2 ]. Поэтому |
|||
имеем |
|
|
|
|
|
∫∫xydxdy = ∫∫xydxdy + ∫∫xydxdy + |
|
||||
D |
D1 |
D2 |
|
|
|
Рис. 1.7 |
|
−1 |
2 − x2 |
||
∫∫xydxdy = |
∫ xdx |
∫ |
ydy + |
||
+ |
|||||
|
D3 |
− 2 |
− 2−x2 |
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
2−x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2−x |
2 |
|
|
||||||
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
−1 |
|
|
y2 |
|
|
|
|
|
|
|
|
|||||||||||
+ ∫ xdx |
|
∫ ydy + ∫ xdx |
|
∫ |
|
ydy = |
|
∫ |
xdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
2 |
− |
|
|
|
||||||||||||
|
− |
2−x |
|
|
|
|
|
|
|
|
− |
2−x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
y2 |
|
x |
|
|
|
|
2 |
|
|
y2 |
|
|
2−x |
|
1 x4 |
|
|
|
|
|
2 − x2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
+ ∫ xdx |
|
|
|
|
|
|
|
|
|
+ ∫ xdx |
|
|
|
|
|
|
|
|
= ∫ x |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
− − |
|
|
|
|
|
− − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
− |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x |
|
|
1 |
1 |
|
|
|
|
|
|
x |
|
|
|
|
1 |
|
x6 |
|
|
x4 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
∫ (x |
|
+ x |
|
− 2x)dx = |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
6 |
|
|
|
4 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Задача 1.1. Вычислить двойные интегралы: а) ∫∫(x2 ) / ( y2 )dxdy; x = 2, y = x, xy = 1;
D
dx =
1
− x2 = 0.
−1
б) ∫∫ cos(x + y)dxdy; x = 0, y = π, y = x;
D
в) ∫∫(x2 + y2 )dxdy; x2 + y2 = 8, y = x, y = −x, y > 0;
D
г) ∫∫(x + y)dxdy; y = x, y = 1, y = x2 / 9;
D
12
д) ∫∫xdxdy, где область D, лежащая в первой четверти, ограни-
D
чена прямой, проходящей через точки (2; 0), (0; 2), и дугой окруж-
ности с центром в точке (0;1) и радиусом 1. |
|
|||||||
Задача 1.2. Записать двойные интегралы от функции |
f ( x, y) |
|||||||
по указанным областям D в виде повторных интегралов: |
|
|||||||
|
|
2 |
|
2 |
|
|
||
а) область D ограничена кривой |
x |
+ |
|
y |
= 1; |
|
||
2 |
2 |
|
||||||
|
|
|
a |
|
b |
|
||
б) область |
D |
ограничена линиями |
|
x = 0, y = 0, x2 + y2 = r2 , |
||||
причем x ≥ 0, y ≥ 0. |
|
|
|
|
|
|
|
|
в) область |
D |
есть параллелограмм |
с вершинами в |
точках |
||||
(−3;1), (2;1), |
(2; 4), (6; 4). |
|
|
|
|
|
|
|
г) область D задана неравенствами y − 2x ≤ 0, 2 y − x ≥ 0, xy ≤ 2.
1.3. Изменение порядка интегрирования
Если область σ является простой как относительно оси Ox, так и относительно оси Oy, то применимы обе формулы — (1.2), (1.3). Следовательно,
|
b |
ϕ2 ( x) |
d |
ψ2 ( y) |
∫∫ f (x, y)dxdy = ∫dx |
∫ |
f (x, y)dy = ∫dy |
∫ f (x, y)dx. |
|
σ |
a |
ϕ1( x) |
c |
ψ1 ( y) |
Иными словами, в рассматриваемом случае повторное интегрирование не зависит от порядка интегрирования. Этим обстоятельством часто пользуются при вычислении двойного интеграла, выбирая ту из двух формул, которая приводит к более простым выкладкам.
В качестве упражнения на расстановку пределов рассмотрим задачу об изменении порядка интегрирования в повторном интеграле
b ϕ2 ( x)
∫dx ∫ f ( x, y)dy.
a ϕ1( x)
13

1. Прежде всего строим область интегрирования σ, которая находится в полосе между прямыми x = a, x = b и ограничена снизу линией y = ϕ1(x), а сверху линией y = ϕ2 (x).
2.Затем область σ проектируем на ось Oy: проекцией будет отрезок [c, d ].
3.Из пункта 2 делаем вывод: прямые y = c, y = d ограничивают снизу и сверху полосу, в которой расположена область σ.
4. Находим левую границу области σ x = ψ1( y) и правую
x= ψ2 ( y).
5.Теперь можем записать исходный повторный интеграл в виде
d ψ2 ( y)
∫dy ∫ f (x, y)dx.
c ψ1 ( y)
Аналогично, если требуется изменить порядок интегрирования в повторном интеграле
d ψ2 ( y)
∫dy ∫ f ( x, y)dx,
c ψ1( y)
то, спроектировав область σ на ось Ox, находим уравнения прямых x = a, x = b, нижнюю и верхнюю границы области σ: y = ϕ1(x), y = ϕ2 (x).
Если область σ не является простой относительно некоторой оси, то можно разбить σ на части, а интеграл — на сумму интегралов по этим частям. Рассмотрим примеры, иллюстрирующие эту ситуацию.
Пример 1.6. В двойном интеграле
∫∫ f ( x, y)dxdy
σ
расставить пределы интегрирования двумя способами, если область σ ограничена прямыми x = 0, x = 1, y = 1 и кривой
y = − 2x − x2 .
14
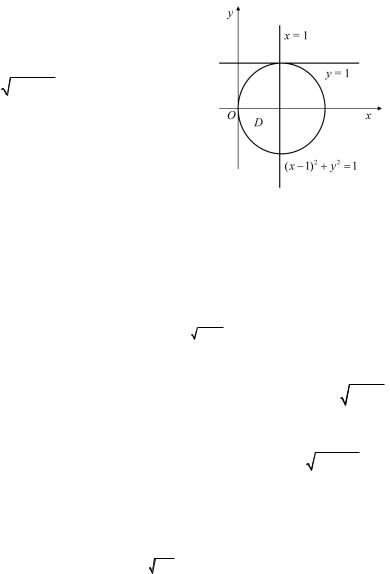
Решение. Область σ находится в |
|
|||
полосе между прямыми |
x = 0, x = 1. |
|
||
Верхняя граница — прямая y = 1, |
|
|||
нижняя граница — дуга окружности |
|
|||
y = − 2x − x2 |
(рис. 1.8). |
|
|
|
Возводя |
обе части |
последнего |
|
|
уравнения |
в |
квадрат, |
получаем: |
|
y2 = 2x − x2 , |
или после выделения |
|
||
полного квадрата в правой части: |
|
|||
y2 = −(x −1)2 +1, y2 + (x −1)2 = 1 — |
|
|||
уравнение |
окружности |
с центром |
Рис. 1.8 |
|
|
||||
(1; 0) и радиусом r = 1.
Рассматривая область σ как простую относительно оси Oy и зная ее верхнюю и нижнюю границы, сведем двойной интеграл к повторному:
|
1 |
|
1 |
∫∫ f (x, y)dxdy = ∫dx |
|
∫ f (x, y)dy. |
|
σ |
0 |
− |
2 |
|
|
2x−x |
|
Область σ является простой относительно оси Oy, но не является |
|||
простой относительно Ox, так как ее левая граница состоит их двух частей: графика функции x = 0 и графика функции x = 1 − 1− y2 .
Правая граница σ является графиком функции x = 1. |
|
Осью Ox разобьем область σ на две части: σ1, σ2 . |
Найдя точку |
пересечения прямой x = 1 с дугой окружности y = − |
2x − x2 , де- |
лаем вывод: область σ1 проектируется на отрезок [−1; 0] оси Oy,
а область σ2 |
— на отрезок [0;1] той же оси. Поэтому имеем: |
||||
|
0 |
|
1 |
1 |
1 |
∫∫ f (x, y)dxdy = ∫dy |
∫ |
f (x, y)dx + ∫dy∫ f (x, y)dx. |
|||
σ |
−1 |
1− |
2 |
0 |
0 |
|
|
1− y |
|
|
|
Пример 1.7. В двойном интеграле
∫∫ f ( x, y)dxdy
σ
15

двумя способами расставить пределы интегрирования по области σ, которая является параллелограммом с вершинами в точках
A(1; 2), B(2; 4), C(2;7), D(1;5).
|
Решение. Найдем уравнения границ области σ. |
|
Записав урав- |
||||||||
нения прямых по двум точкам, убеждаемся в том, что прямая AB |
|||||||||||
имеет уравнение |
y = 2x, прямая BC: x = 2, прямая CD: y = 2x + 3, |
||||||||||
прямая DA: x = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Область |
σ лежит |
в |
полосе между |
|||
|
|
|
|
|
прямыми x = 1, x = 2 и ограничена свер- |
||||||
|
|
|
|
|
ху прямой |
y = 2x + 3, |
а |
снизу прямой |
|||
|
|
|
|
|
y = 2x (рис. 1.9). Поэтому |
|
|
|
|||
|
|
|
|
|
|
|
2 2x+3 |
|
|||
|
|
|
|
|
∫∫ f (x, y)dxdy = ∫dx ∫ |
|
f (x, y)dy. |
||||
|
|
|
|
|
σ |
|
1 |
2x |
|
|
|
|
|
|
|
|
Для того чтобы расставить пределы в |
||||||
|
Рис. 1.9 |
|
|
|
другом порядке, разобьем область σ на |
||||||
|
|
|
|
|
три части: |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
σ1 |
2 ≤ y ≤ 4,1 ≤ x |
≤ |
|
|
,σ2 {4 ≤ y ≤ 5,1 ≤ x ≤ 2}, |
|
|
|
|
||
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
y − 3 |
|
|
|
|
|
|
|
|
σ3 5 ≤ y |
≤ 7, |
|
≤ x ≤ 2 . |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
Применяя формулу (1.3) для каждой из этих областей, получаем: |
||||||||||
|
4 |
|
y /2 |
5 |
2 |
|
|
|
|
|
|
∫∫ f (x, y)dxdy = ∫dy ∫ f (x, y)dx + ∫dy∫ f (x, y)dx + |
|
|
|
|
|||||||
σ |
2 |
|
1 |
4 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
2 |
|
|
|
|
|
|
|
|
|
+∫dy |
|
∫ |
f ( x, y)dx. |
|
|
|
|
|
|
|
|
|
5 |
( y−3)/ 2 |
|
|
Пример 1.8. Изменить порядок интегрирования в повторном интеграле
1 2−x2
∫dx ∫ f ( x, y)dy.
0 x
16
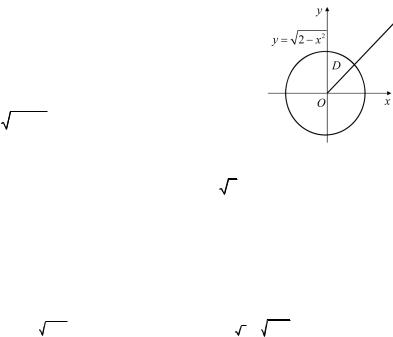
Решение. Исходя из пределов в по- |
|
|||
вторном интеграле можно изобразить об- |
|
|||
ласть σ. Действительно, она расположена |
|
|||
в полосе между прямыми |
x = 0, x = 1. |
|
||
Нижняя граница области σ задается урав- |
|
|||
нением y = x, верхняя — |
уравнением |
|
||
y = 2 − x2 (рис. 1.10). |
|
|
|
|
Последнее уравнение задает на плос- |
|
|||
2 |
+ y |
2 |
= 2 с цен- |
Рис. 1.10 |
кости дугу окружности x |
|
|
||
тром в начале координат и радиусом 2. |
|
|||
Она пересекается с нижней границей области σ |
(т. е. с прямой |
|||
y = x ) в точке B(1;1). Область σ является простой относительно оси Oy, но относительно оси Ox она не является простой, так как ее правая граница состоит из дуги окружности и отрезка прямой.
Поэтому приходится разбивать область σ на две части прямой y = 1, а интеграл — на сумму интегралов:
1 |
2−x2 |
1 |
|
2 |
2− y |
2 |
y |
|
|||||
∫dx ∫ |
f (x, y)dy = ∫dy∫ f (x, y)dx + ∫ dy ∫ |
f (x, y)dx. |
||||
0 |
x |
0 |
0 |
1 |
0 |
|
Пример 1.9. Изменить порядок интегрирования в повторном |
||||||
интеграле |
|
|
|
|
|
|
2 |
3 |
4 |
10−x |
7 |
10−x |
|
x |
|
|||||
∫dx ∫ f ( x, y)dy + ∫dx ∫ f ( x, y)dy + ∫dx ∫ f ( x, y)dy. |
||||||
0 |
0 |
2 |
0 |
4 |
x−4 |
|
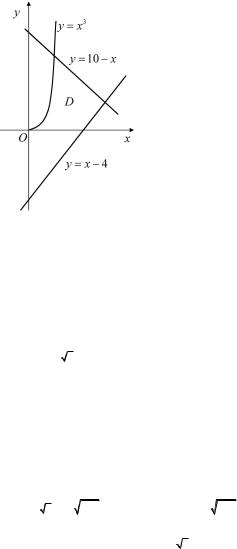
Решение. Нетрудно изобразить на координатной плоскости об- |
||||||
ласть σ, |
по которой вычисляется двойной интеграл. Она разбита |
|||||
на три части: σ1, σ2 , σ3. Область σ1 |
ограничена прямыми x = 0, |
|||||
y = 0, x = 2 и кубической параболой |
y = x3 |
, область σ2 — пря- |
||||
мыми y = 0, x = 2, x = 4, |
y = 10 − x, |
область |
σ3 — прямыми |
|||
y = 10 − x, x = 4, x = 7, y = x − 4 (рис. 1.11).
17
|
|
Область σ не является простой относи- |
||||
|
тельно оси Ox, так как ее правая граница |
|||||
|
состоит |
из |
отрезков двух прямых: |
|||
|
y = 10 − x |
и |
y = x − 4. Поэтому для пере- |
|||
|
мены порядка интегрирования необхо- |
|||||
|
димо разбить область σ на две простые |
|||||
|
части: σ1′ |
и σ2′ , имеющие общей грани- |
||||
|
цей |
прямую |
y = 3 |
(точка |
пересечения |
|
|
прямых y = 10 − x, y = x − 4 |
имеет коор- |
||||
|
динаты (7; 3)). Тогда получим: |
|||||
|
|
∫∫ f (x, y)dxdy = ∫∫ f (x, y)dxdy + |
||||
Рис. 1.11 |
|
|
|
|
1 |
|
|
|
σ |
|
|
σ ′ |
|
|
3 |
y+4 |
|
8 |
10− y |
|
+ ∫∫ f (x, y)dxdy = ∫dy ∫ f (x, y)dx + ∫dy |
∫ f (x, y)dx. |
|||||
σ2′ |
0 |
1/3 |
|
3 |
1/3 |
|
y |
|
y |
|
|||
Задача 1.4. Изменить порядок интегрирования в повторных интегралах:
4 |
x |
|
|
|
|
а) ∫dy ∫ f ( x, y)dx; |
|
|
|||
0 |
x/2 |
|
|
|
|
2 |
2− y |
|
|
|
|
б) ∫ dy ∫ |
f ( x, y)dx; |
|
|
||
−6 |
2 |
− |
|
|
|
|
y |
/4 1 |
|
|
|
0 |
3 |
|
3 |
3 |
|
в) ∫ dx ∫ f (x, y)dy + ∫dx∫ f (x, y)dy; |
|||||
−3 |
− x |
|
0 |
x |
|
|
|
1− y |
2 |
|
2 |
2 /2 |
|
|
0 |
1− y |
|
г) ∫ dy ∫ |
f ( x, y)dx + ∫ dy ∫ f ( x, y)dx; |
||||
0 |
|
y |
|
− 2 /2 |
− y |
π |
sin x |
|
|
|
|
д) ∫dx ∫ f ( x, y)dy; |
|
|
|||
0 |
0 |
|
|
|
|
18

|
2 |
2 |
a |
a −x |
|
е) ∫dx |
∫ |
f ( x, y)dy; |
0 |
(a2 −x2 )/2a |
|
1 |
2 |
|
3− y |
|
|
ж) ∫dy ∫ f ( x, y)dx. |
||
0 |
y2 /2 |
|
Задача 1.5. Расставить пределы интегрирования в том и другом порядке в двойном интеграле
∫∫ f ( x, y)dxdy,
D
если область D ограничена указанными линиями: а) y = sin x, y = cos x, y = 0, 0 ≤ x ≤ π / 2;
б) y = ex , y = e2x , x = 1;
в) |
y = 3 / x, x2 + y2 = 10, x > 0; |
г) |
y = ln x, x = 2, y = 0. |
2. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ
Вычисление двойного интеграла нередко можно упростить с помощью замены переменных. Пусть функции
u |
= u(x, y), |
|
(2.1) |
v |
= v(x, y) |
определены на всей плоскости xOy или в некоторой ее области σ
и имеют непрерывные частные производные в области σ. Допустим также, что выписанную систему уравнений можно однозначно разрешить относительно x и y :
x = x(u, v); |
|
|
(2.2) |
y = y(u, v), |
|
19
тогда каждой точке M ( x, y) из области σ будет взаимнооднозначно соответствовать пара чисел (u, v), называемых криволинейными координатами этой точки. Если область σ расположена в той части плоскости xOy, в которой введены криволинейные координаты u, v, то справедлива следующая формула:
∫∫ f ( x, y)dxdy = ∫∫ f [ x(u, v), y(u, v)] | J (u, v) | dudv, |
(2.3) |
|
σ |
σ′ |
|
где σ′ — область изменения криволинейных координат u, v, отвечающая области σ; J (u,v) — якобиан преобразования (2.2), не равный нулю ни в одной точке области σ′ :
|
∂x |
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
∂y |
|
∂x |
|
∂y |
|
J (u,v) = |
∂u |
∂v |
= |
|
− |
|
≠ 0. |
||||||
∂y |
|
∂y |
|
|
|
|
|||||||
|
|
|
∂u ∂v ∂v ∂u |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂u |
∂v |
|
|
|
|
|
|
|
|
|
||
Если подынтегральная функция или уравнение границы области интегрирования содержит сумму x2 + y2 , то в большинстве случаев упрощение интеграла достигается преобразованием его к полярным координатам. Это объясняется тем, что указанная сумма в полярных координатах имеет простой вид:
(ρcosϕ)2 + (ρsin ϕ)2 = ρ2 .
Если в состав подынтегральной функции или уравнения границы области интегрирования входит сумма ax2 + by2 , a > 0, b > 0, то пользуются обобщенной полярной системой координат:
|
|
|
|
x = |
|
|
ρ |
cosϕ; |
y = |
ρ |
sin ϕ. |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
a |
|
|
b |
|
|
|
|
|||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
ρ |
|
2 |
ρ |
2 |
= ρ |
2 |
|
||||
ax |
|
+ by |
|
= a |
|
|
|
cosϕ |
+ b |
|
sin ϕ |
|
, |
||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
a |
|
|
b |
|
|
|
|
||||
20
