
Bezverkhniy_Kratnye_integraly_2014
.pdf
аякобиан преобразования в этом случае J (ρ,ϕ) = ρ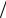 ab .
ab .
Вполярных координатах формулы (1) имеют вид:
x = ρcos ϕ; |
|
|
(2.4) |
y = ρsin ϕ. |
|
Отметим, что система (2.4) осуществляет переход от прямоугольных координат x, y к полярным координатам ρ, ϕ при условии, что полюс помещен в начале координат, а полярная ось направлена вдоль оси Ox. В этом случае | J |= ρ, и формула (2.3) принимает вид
∫∫ f (x, y)dxdy = ∫∫ f (ρcos ϕ, ρsin ϕ)ρdϕdρ.
σ σ′
Если область σ ограничена лучами, образующими с полярной осью углы ϕ1 < ϕ2 , и кривыми ρ = ρ1(ϕ), ρ = ρ2 (ϕ), то соответствующие этой области полярные координаты изменяются в пределах {ϕ1 ≤ ϕ ≤ ϕ2 ; ρ1(ϕ) ≤ ρ ≤ ρ2 (ϕ)}, и
|
ϕ2 |
ρ2 (ϕ) |
|
∫∫ f (x, y)dxdy = ∫ dϕ ∫ f (ρcosϕ, ρsin ϕ)ρdρ. |
(2.5) |
||
σ |
ϕ1 |
ρ1 (ϕ) |
|
Если область σ охватывает начало координат, то
|
2π |
ρ(ϕ) |
|
∫∫ f (x, y)dxdy = ∫ dϕ ∫ f (ρcosϕ, ρsin ϕ)ρdρ, |
(2.6) |
||
σ |
0 |
0 |
|
где ρ = ρ(ϕ) — полярное уравнение кривой, ограничивающей об-
ласть σ. Формулы (2.5), (2.6) удобно использовать при вычислении интеграла по области σ, являющейся кругом или сектором круга.
Пример 2.1. Вычислить двойной интеграл
∫∫ 1 − (x2 + y2 )dxdy,
σ
если область σ ограничена окружностью x2 + y2 = 1.
21
Решение. Область σ есть круг единичного радиуса с центром в начале координат. Введем полярные координаты. В полярных координатах имеет место равенство x2 + y2 = ρ2 (см. формулу (2.4)), и уравнение окружности принимает вид ρ = 1. Тогда по формуле (2.6) получим
|
2π |
1 |
∫∫ |
1 − (x2 + y2 )dxdy = ∫ dϕ∫ 1 − ρ2 ρdρ = |
|
σ |
0 |
0 |
2π |
1 |
|
|
1− ρ2 |
|
1 |
2π (1 |
− ρ2 )3/2 |
|
1 |
|
1 |
2π |
1 |
|
|
2π |
||
|
|
|
|
|
|
||||||||||||||
2 |
|
|
|
|
|
|
|||||||||||||
= ∫dϕ∫ |
1− ρ |
d |
|
= − |
|
∫ |
|
|
|
|
dϕ = |
|
∫dϕ = |
|
|
ϕ |
|
|
|
−2 |
2 |
|
3 / 2 |
|
3 |
3 |
|||||||||||||
0 |
0 |
|
|
|
0 |
|
0 |
|
0 |
|
|
0 |
|||||||
|
|
|
|
||||||||||||||||
Пример 2.2. Вычислить двойной интеграл
∫∫ydxdy,
σ
=2π .
3
если область σ ограничена верхней половиной дуги окружности x2 + y2 = ax и отрезком оси Ox от точки с абсциссой 0 до точки с абсциссой a (рис. 2.1).
|
|
Решение. |
Область |
σ |
— |
полукруг. |
|
|
Введем полярные координаты. Уравнение |
||||
|
|
окружности, ограничивающей область σ, |
||||
|
|
в полярных координатах принимает вид |
||||
|
|
ρ2 = ρacosϕ, |
или ρ = a cosϕ. |
Подынте- |
||
|
|
гральная функция имеет вид |
y = ρsin ϕ. |
|||
Рис. 2.1 |
|
Угол ϕ изменяется от 0 до π/2 (полукруг |
||||
|
|
|
|
|
|
|
|
|
находится в первой четверти). При каж- |
||||
|
|
дом фиксированном значении угла ϕ ра- |
||||
диус ρ изменяется от 0 (в начале координат) до |
ρ = acosϕ (на |
|||||
окружности). Тогда по формуле (2.5) получаем: |
|
|
|
|||
|
π/2 |
acosϕ |
π/2 |
acosϕ |
|
|
∫∫ydxdy = ∫ dϕ |
∫ ρsin ϕρdρ = ∫ sin ϕdϕ |
∫ |
ρ2dρ = |
|||
σ |
0 |
0 |
0 |
0 |
|
|
22

π/2 |
|
3 |
|
acosϕ |
|
a |
3 π/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= ∫ |
sin ϕ |
ρ |
|
|
|
dϕ = |
|
∫ sin ϕcos3ϕdϕ = |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
0 |
3 |
|
|
|
3 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
3 π/2 |
|
|
|
3 |
4 |
|
π/2 |
3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
a |
|
|
a |
|
||||||
|
|
|
|
|
|
|
|
|
= − |
|
∫ |
cos |
3ϕd cosϕ = − |
|
cos |
ϕ |
|
= |
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
3 |
0 |
|
3 |
4 |
|
|
12 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
Пример 2.3. В двойном интеграле
∫∫ f ( x, y)dxdy
σ
расставить пределы интегрирования в полярных координатах, если
область |
σ является квадратом с вершинами в точках O(0; 0), |
A(1; 0), |
B(1;1), C(0;1). |
Решение. Уравнение стороны AB (x = 1) в полярных координатах принимает вид ρcosϕ = 1, или ρ = 1 / cosϕ. Уравнение стороны
BC ( y = 1) принимает вид ρ = 1 / sin ϕ. Угол ϕ изменяется от 0 до
π / 2 |
(квадрат находится в первой четверти). При изменении угла |
||
от 0 |
до |
π / 4 |
ρ меняется от 0 до ρ = 1 / cosϕ, а при изменении |
угла от |
π / 4 |
до π / 2 ρ изменяется от 0 до ρ = 1 / sin ϕ. Область |
|
интегрирования не является простой и приходится разбивать ее на две части, поскольку верхнюю границу интегрирования нельзя задать одной формулой. Следовательно,
|
π/4 |
1/cosϕ |
|
|
|
|
|
|
∫∫ f (x, y)dxdy = |
∫ dϕ |
∫ f (ρcosϕ, ρsin ϕ)ρdρ + |
||||||
σ |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
π/2 1/sin ϕ |
||
|
|
|
|
|
|
+ ∫ dϕ |
∫ f (ρcosϕ, ρsin ϕ)ρdρ. |
|
|
|
|
|
|
|
π/4 |
0 |
|
Пример 2.4. Вычислить двойной интеграл |
||||||||
|
|
|
2 |
2 |
|
|
||
|
|
∫∫ |
1 − |
x |
− |
y |
dxdy, |
|
|
|
2 |
2 |
|
||||
|
|
|
|
a |
|
b |
|
|
σ
23

|
|
2 |
2 |
|
|
если область σ ограничена эллипсом |
x |
|
+ |
y |
= 1. |
a |
2 |
2 |
|||
|
|
|
b |
||
Решение. Для решения этой задачи удобно ввести обобщенные полярные координаты, положив
x = aρcos ϕ;y = bρsin ϕ.
Найдем якобиан данного преобразования. Очевидно, что
J = |
a cosϕ |
−aρsin ϕ |
= abρ |
cosϕ −sin ϕ |
= |
||
bsin ϕ |
bρcosϕ |
sin ϕ |
cosϕ |
||||
|
|
|
|||||
= abρ(cos2ϕ + sin 2ϕ) = abρ и | J |= abρ.
Подынтегральная функция в обобщенных полярных координатах принимает вид
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
1 − |
x |
|
− |
y |
= |
1 − ρ2 cos2ϕ − ρ2 sin2ϕ = |
||||||
a |
2 |
2 |
||||||||||
|
|
|
b |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
= |
1 − ρ2 (cos2ϕ + sin 2ϕ) = 1 − ρ2 . |
|
Теперь по формуле (2.3) имеем |
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
∫∫ |
1 − |
x |
− |
y |
dxdy = ∫∫ |
1 − ρ2 abρdρdϕ. |
|
|
|
|
|
|
2 |
2 |
||||||
|
|
|
|
|
σ |
|
a |
|
b |
|
σ′ |
|
Так как начало полярной оси содержится внутри области σ′, то угол ϕ изменяется от 0 до 2π. Уравнение эллипса в обобщенных полярных координатах принимает вид ρ = 1. Поэтому ρ изменяется от 0 до 1. Тогда
|
|
|
2 |
2 |
|
2π |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
∫∫ |
1 − |
x |
|
− |
y |
dxdy = ab ∫ dϕ∫ 1 − ρ2 ρdρ = |
|
|
|
|
|||||||||||
a |
2 |
2 |
|
|
|
|
|||||||||||||||
σ |
|
|
|
b |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
2π |
1 (1 |
2 |
) |
3/2 |
|
1 |
|
ab |
2π |
ab |
|
2π |
|||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
= ab ∫ − |
− ρ |
|
|
|
|
dϕ = |
∫ dϕ = |
ϕ |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
0 |
2 |
|
|
3 / 2 |
|
|
|
0 |
3 |
0 |
3 |
|
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= 2πab . 3
24
Пример 2.5. Вычислить двойной интеграл
|
|
|
|
2 |
|
|
2 |
|
|
|
|
I = ∫∫ |
1 |
− x |
− y |
|
|
dxdy, |
|||
|
|
2 |
+ y |
2 |
|
|||||
|
|
σ |
1 + x |
|
|
|
|
|||
где σ — верхний полукруг x2 + y2 ≤ 1. |
||||||||||
Решение. Преобразуем |
интеграл |
|
|
к полярным координатам: |
||||||
x = ρcosϕ, y = ρsin ϕ. Тогда |
|
|
|
|
|
|
|
|
||
|
|
|
2 |
2 |
|
|
2 |
|
||
x2 + y2 = ρ2 ; |
|
1 − x |
− y |
= |
|
1 − ρ |
; J (ρ,ϕ) = ρ, |
|||
|
2 |
2 |
2 |
|||||||
|
1 + x |
|
+ y |
|
|
1 + ρ |
||||
и данный интеграл принимает вид |
|
|
|
|
|
|
||||
|
|
|
|
|
2 |
|
|
|
|
|
|
I = ∫∫ |
|
1 − ρ |
ρdρdϕ. |
||||||
|
|
2 |
||||||||
|
|
σ′ |
|
1 + ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим область интегрирования σ. Уравнение ее границы в полярных координатах принимает вид ρ = 1. В пределах данной области полярный угол x = ρcos ϕ изменяется от 0 до π, а полярный радиус изменяется от 0 до 1 (при любом фиксированном ϕ луч, исходящий из полюса и пересекающий область σ, имеет на границе области две точки: при ρ = 0 и при ρ = 1 ). Следовательно,
|
1 − ρ2 |
π |
1 |
1 − ρ2 |
1 |
1 − ρ2 |
|
I = ∫∫ |
|
ρdρdϕ = ∫dϕ∫ |
|
ρdρ = π∫ |
|
ρdρ. |
|
1 + ρ2 |
1 + ρ2 |
1 + ρ2 |
|||||
σ′ |
|
0 |
0 |
|
0 |
|
|
Вычисляя интеграл методом внесения под знак дифференциала, получаем:
I= π (π − 2). 2
Пример 2.6. Вычислить двойной интеграл
dxdy
I = ∫∫ (x2 + y2 )2 ,
σ
25
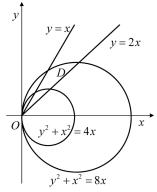
где |
область σ ограничена |
окружностями |
x2 + y |
2 = 4x, |
x2 + y |
2 = 8x и прямыми y = x, y = 2x (рис. 2.2). |
|
|
|
|
|
Решение. Перейдем к полярным |
||
|
координатам. Тогда |
подынтеграль- |
||
|
ная |
функция |
примет |
вид |
|
f (x, y) = (x2 + y2 )−2 = ρ−4. |
Криво- |
||
|
линейные участки границы области |
|||
|
σ задаются уравнениями: |
|
||
|
ρ2 cos2ϕ + ρ2 sin 2ϕ = 4ρcos ϕ |
|
||
|
|
|
или ρ = 4cosϕ; |
|
|
ρ2 cos2ϕ + ρ2 sin 2ϕ = 8ρcos ϕ |
|
||
|
Рис. 2.2 |
|
или ρ = 8cosϕ; |
|
апрямолинейные участки задаются уравнениями:
ρsin ϕ = ρcosϕ, или tg ϕ = 1, откуда ϕ = π / 4;
ρsin ϕ = 2ρcosϕ, или tg ϕ = 2, откуда ϕ = arctg 2.
Итак, угол ϕ изменяется в постоянных пределах от π / 4 до arctg 2. Чтобы найти пределы изменения ρ, пересечем область σ лучом, исходящим из полюса. Он пересечет границы ρ = 4cosϕ и ρ = 8cosϕ. Следовательно, 4 cos ϕ — нижняя граница интегрирования, 8cosϕ — верхняя граница.
Так как при рассмотренной замене координат в двойном интеграле якобиан равен J = ρ, то
arctg 2 |
8cosϕ |
arctg 2 |
8cosϕ dρ |
||
I = ∫ dϕ ∫ ρ−4ρdρ = |
∫ dφ ∫ |
|
. |
||
3 |
|||||
π/4 |
4cosϕ |
π/4 |
4cosϕ |
ρ |
|
Вычислив этот интеграл, получим I = 3 / 128. Пример 2.7. В двойном интеграле
∫∫ f ( x, y)dxdy,
σ
26
где σ — общая часть двух кругов x2 + y2 ≤ ax, x2 + y2 ≤ by, перейти к полярным координатам и расставить пределы интегрирования.
Решение. В полярных координатах уравнения границ данных кругов принимают вид: ρ = acosϕ, ρ = bsin ϕ.
Пусть окружности ρ = a cosϕ, ρ = bsin ϕ пересекаются в точках
A, O. Хорда AO делит область интегрирования на две части: σ1 и
σ2. Тогда
I = I1 + I2 = ∫∫ f (x, y)dxdy + ∫∫ f (x, y)dxdy.
σ1 σ2
Тангенс угла ϕ0 , образованного хордой AO и осью Ox, равен
a / b, |
что следует из уравнения acosϕ0 = bsin ϕ0 для общих точек |
||
окружностей ρ = acosϕ, ρ = bsin ϕ. Поэтому |
|||
arctg(a/b) |
bsin ϕ |
|
|
I = |
∫ dϕ |
∫ f (ρcosϕ, ρsin ϕ)ρdρ + |
|
|
0 |
0 |
|
|
|
π/2 |
a cosϕ |
|
|
+ ∫ d φ |
∫ f (ρcos ϕ, ρsin ϕ)ρdρ. |
|
|
arctg(a/b) |
0 |
Задача 2.1. В следующих двойных интегралах перейти к полярным координатам и расставить пределы интегрирования:
а) I = ∫∫ f (x, y)dxdy, где σ — круг x2 + y2 ≤ ax;
σ
б) ∫∫ f ( x, y)dxdy, где σ — треугольник, ограниченный прямы-
σ
ми y = x, y = −x, y = 1;
в) ∫∫ f ( x, y)dxdy, где σ — кольцо, ограниченное окружностя-
σ
ми радиусов 1 и 2 с центром в начале координат;
г) ∫∫ f ( x, y)dxdy, где σ — область, ограниченная лемнискатой —
σ
кривой с уравнением (x2 + y2 )2 = 2a2 xy;
27
д) ∫∫ f ( x, y)dxdy, |
где |
σ |
— |
область, |
ограниченная |
кривой |
σ |
|
|
|
|
|
|
(x2 + y2 )3 = a2 (x4 + y4 ); |
|
|
|
|
|
|
е) ∫∫ f ( x, y)dxdy, |
где |
σ |
— |
область, |
ограниченная |
кривой |
σ |
|
|
|
|
|
|
(x2 + y2 )2 = 2ax3 .
Задача 2.2. Преобразовать с помощью подстановки x = aρcosϕ,
y = bρsin ϕ интеграл |
|
|
|
|
|
|
|
|
∫∫ f |
|
|
x |
2 |
|
y |
2 |
|
|
9 − |
|
− |
|
|
|||
|
|
|
|
|||||
|
a |
2 |
b |
2 |
dxdy, |
|||
σ |
|
|
|
|
|
|
||
|
|
|
|
|
|
где σ — область, лежащая в первом квадранте часть эллиптического кольца, ограниченного эллипсами
x2 |
+ |
y2 |
= 1, |
x2 |
+ |
y2 |
= 4. |
|
a2 |
b2 |
a2 |
b2 |
|||||
|
|
|
|
Задача 2.3. двойные интегралы преобразовать к полярным координатам:
R |
R2 −x2 |
|
|
|
|
|
|
|
|
а) ∫dx |
|
∫ |
f (x, y)dxdy; |
|
|
|
|||
0 |
|
0 |
|
|
|
|
|
|
|
2R |
|
2Ry− y2 |
|
|
|
|
|
|
|
б) ∫ dy |
∫ |
|
f ( x, y)dx; |
|
|
|
|||
R/2 |
|
0 |
|
|
|
|
|
|
|
R/( 1+R2 ) |
Rx |
|
x |
|
R |
|
|||
в) |
∫ |
dx ∫ f |
|
dy + |
|
∫ dx |
|||
|
|
||||||||
|
0 |
|
0 |
|
y |
R/ |
1+R |
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
R2 −x2
∫
0
|
x |
|
f |
|
dy. |
|
||
|
y |
|
28
3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР
Площадь плоской области σ на плоскости xOy вычисляют по формуле
|
|
|
S = ∫∫dxdy. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
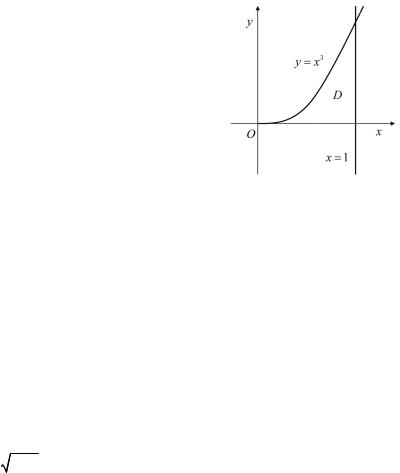
Пример 3.1. Вычислить площадь |
|
|
|
|
|
|
|
|
|
||||||
плоской области σ, ограниченной |
|
|
|
|
|
|
|
|
|
||||||
прямыми y = 0, x = 1 |
и кубической |
|
|
|
|
|
|
|
|
|
|||||
параболой y = x3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Область |
σ проектиру- |
|
|
|
|
|
|
|
|
|
|||||
ется на ось Ox |
в отрезок [0;1]. |
|
|
|
|
|
|
|
|
|
|||||
Нижней границей области |
σ |
явля- |
|
|
|
|
|
|
|
|
|
||||
ется прямая y = 0, |
а верхней — ку- |
|
|
|
|
|
|
|
|
|
|||||
бическая парабола |
|
3 |
область |
|
|
|
|
|
|
|
|
|
|||
y = x , |
|
|
|
|
|
|
|
|
|
||||||
является простой относительно обе- |
|
|
|
|
|
|
|
|
|
||||||
их осей, поэтому порядок интегри- |
|
|
|
Рис. 3.1 |
|||||||||||
рования можно выбрать произволь- |
|
|
|
|
|
|
|
|
|
||||||
ным образом (рис. 3.1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x3 |
1 |
|
x3 |
1 |
|
x |
4 |
|
1 |
1 |
|
||
|
|
|
|
||||||||||||
S = ∫∫dxdy = ∫dx ∫dy = ∫y |
|
dx = ∫x3dx = |
|
|
|
|
= |
. |
|||||||
|
|
|
|
|
|||||||||||
|
0 |
0 |
0 |
|
|
0 |
4 |
|
|
4 |
|
||||
σ |
|
0 |
|
|
|
|
|
0 |
|
|
|||||
Пример 3.2. Вычислить площадь плоской области σ, ограни- |
|||||||||||||||
ченной прямой y = 2 и параболой y = x2 −1. |
|
|
|
|
|
|
|
|
|
||||||
Решение. Область |
σ является |
простой |
относительно обеих |
||||||||||||
осей. Она симметрична относительно оси Oy, |
поэтому достаточно |
||||||||||||||
вычислить площадь ее правой половины. Она проектируется на отрезок [−1; 2] оси Oy, ее левой границей служит прямая x = 0, а
правой — парабола y = x2 −1, а точнее, правая ее ветвь, т. е. линия x = y +1 (рис. 3.2). Итак,
29
S |
2 |
y+1 |
2 |
|
y+1 |
2 |
|
2 |
|
2 |
|
|
|
|
|||||||
= ∫ dy |
∫ dx = ∫ x |
|
|
dy = ∫ |
y +1dy = |
( y +1)3/ 2 |
= 2 3, |
|||
|
|
|
|
|||||||
2 |
−1 |
0 |
−1 |
|
|
−1 |
3 |
|
−1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
откуда S = 4 3.
Рис. 3.2 |
Рис. 3.3 |
|
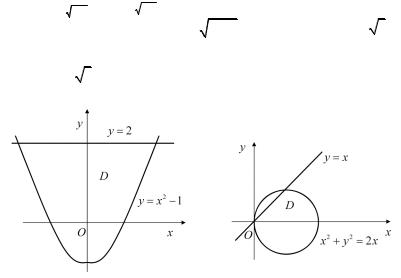
Пример 3.3. Вычислить площадь плоской области σ, ограни- |
||
ченной прямыми y = 0, y = x и окружностью x2 + y |
2 = 2x. |
|
Решение. Введем полярные координаты. Уравнение окружно- |
||
сти, ограничивающей |
область σ примет вид: |
ρ2 2ρcosϕ или |
ρ = 2cosϕ. Так как область σ заключена между прямыми y = x, y = 0, то угол ϕ изменяется от 0 до π / 4. При этом ρ меняется от
0 до 2 cos y = x (рис. 3.3). Поэтому получаем:
π/4 |
2cosϕ |
π/4 |
ρ |
2 |
|
2cosϕ |
π/4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
S = ∫ dφ |
∫ ρdρ = ∫ |
|
|
|
|
dϕ = 2 ∫ cos2ϕdϕ = |
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 |
0 |
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
π/4 |
|
|
|
sin 2ϕ |
|
π/4 |
π |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
= ∫ (1 + cos 2ϕ)dϕ |
ϕ + |
|
|
+ |
|
|||||||||
|
|
|
|
= |
|
|
|
|
= |
|
. |
|||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
0 |
|
|
|
2 |
|
|
0 |
4 |
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 3.4. Вычислить площадь плоской области σ, |
ограни- |
|||||||||||||||||
ченной кривой (x |
2 + y2 )2 = 2ax3 (a > 0). |
|
|
|
|
|
|
|
|
|
|
|||||||
30
