Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Bezverkhniy_Kratnye_integraly_2014

.pdf

Скачиваний:

100

Добавлен:

23.03.2016

Размер:

4.48 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

Решение. Введем полярные координаты.
Уравнение кривой, ограничивающей об-
ласть σ, имеет вид ρ4 = 2aρ3 cos3 ϕ	или
ρ = 2aρcos3 ϕ. Область σ симметрична от-
носительно оси Ox и расположена в правой		Рис. 3.4
полуплоскости относительно оси Oy,	по-

скольку из уравнения видно, что x ≥ 0 (рис. 3.4). Для решения задачи достаточно вычислить площадь верхней половины области σ и удвоить результат.

Для верхней половины области σ угол ϕ изменяется от 0 до

π / 2,

а ρ — от 0 до 2aρcos3 ϕ. Поэтому

π/2

2acos

∫ dϕ

∫

∫ ρ2

2acos ϕ

dϕ = 2a2

∫ cos6ϕdϕ =

ρdρ =

2 π/2

∫ (1 + cos 2ϕ)3 dϕ =

∫ (1 + 3cos 2ϕ + 3cos2 2ϕ + cos3 2ϕ)dϕ =

π/2

3 π/2

ϕ +

sin 2ϕ

∫ (1 + cos 4ϕ)dϕ +

π/2

sin 4ϕ

π/2

∫ (1

− sin

2ϕ)d sin 2ϕ =

ϕ +

sin

32ϕ

π/2

πa2

3πa2

5πa2

sin 2ϕ −

откуда S = 5πa2 / 8.

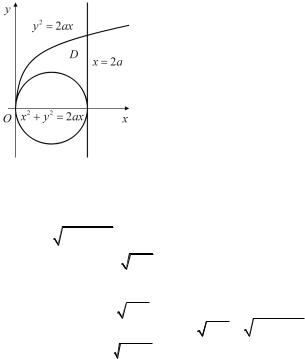
			Пример 3.5. Вычислить площадь об-
			ласти, лежащей в первом квадранте, огра-
			ниченной окружностью x2 + y2 = 2ax, па-
			раболой y2 = 2ax и прямой x = 2a.
			Решение. Внешние пределы интегри-
			рования удобнее выбрать по	x,		так как в
			противном случае область пришлось бы
			разбивать на три части и вычислять три
			интеграла. Область проектируется в отре-
Рис. 3.5			зок [0; 2a] оси Oy, поэтому пределы инте-
			грирования по x равны 0 и 2a (рис. 3.5).
Снизу область ограничена полуокружностью, уравнение кото-
рой y =	2ax − x2 . Сверху она ограничена ветвью параболы, урав-
нение которой y =		2ax.
Таким образом, получим:
	2a	2ax	2a	8a	2		πa	2
S = ∫∫dxdy = ∫ dx		∫	dy = ∫ ( 2ax − 2ax − x2 )dx =	8a		−	πa		.
S = ∫∫dxdy = ∫ dx		∫	dy = ∫ ( 2ax − 2ax − x2 )dx =	3		−			.
σ	0	2	0	3		2
		2ax−x

Здесь первый интеграл табличный, а второй сводится к табличному выделением под корнем полного квадрата.

Пример 3.6. Вычислить площадь области σ, ограниченной кривой (x2 + y2 )2 = 2a2 (x2 − y2 ) с помощью преобразования к полярным координатам.

Решение. В полярных координатах уравнение границы области σ имеет вид

(ρ2 )2 = 2a2ρ2 (cos2ϕ − sin 2ϕ),

ρ4 = 2a2ρ2 cos 2ϕ; ρ2 = 2a2 cos 2ϕ.

Из уравнения ясно, что cos 2ϕ > 0, значит, угол ϕ изменяется от

−π / 4 до π / 4 и от 3π / 4 до 5π / 4. Из уравнения кривой в прямоугольных координатах ясно, что кривая симметрична относительно

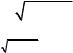
начала координат. Поэтому площадь области σ равна удвоенной площади части области σ, лежащей в правой полуплоскости.

Площадь вычислим по формуле

S= ∫∫dxdy = ∫∫ρdρdϕ.

σσ′

Для той части области σ,						которая лежит в правой полуплоско-
сти относительно оси Oy, угол ϕ меняется от −π / 4								до π / 4,
а ρ — от 0 до a				2cos 2ϕ. Поэтому
	π/4	a	2cos 2ϕ		π/4		π/4
							π/4

S = 2 ∫		dφ	∫	ρdρ =	∫	2a2 cos 2ϕdϕ = a2 sin 2ϕ		= 2a2 .
	−π/4		0		−π/4		−π/4
							−π/4
Задача 3.1. Найти площади областей, ограниченных следую-
щими линиями:
а)	xy = 4, x + y − 5 = 0;
б)	y = sin x, y = cos x, y = 0, 0 ≤ x ≤ π / 2;
в) y = ex , y = e2x , x = 1;
г) y = 2x − x2 , y = x2 ;
д)	y = ln x, x = 2, y = 0.

4. ВЫЧИСЛЕНИЕ ОБЪЕМОВ

Объем цилиндрического тела, ограниченного сверху поверхно-

стью z = f (x, y), а снизу — областью σ плоскости xOy,	находят
по формуле
V = ∫∫ f (x, y)dxdy.	(4.1)
σ

Если тело не является цилиндром, то его разбивают на цилиндрические части.

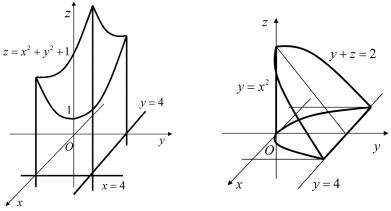
Пример 4.1. Вычислить объем тела, ограниченного плоскостями x = 0, y = 0, z = 0, x = 4, y = 4 и параболоидом z = x2 + y2 +1.

Решение. В данной задаче область σ является прямоугольником, ограниченным прямыми x = 0, y = 0, x = 4, y = 4. Сверху те-

ло ограничено поверхностью z = x													2 + y		2 +1 (рис. 4.1). По формуле
(4.1) имеем
								4		4
V = ∫∫(x2 + y2 +1)dxdy = ∫dx∫(x2 + y2 +1)dy =
σ								0		0
4		2						y3				4	4			2				64
4		2						y3				4	4			2				64
= ∫ (x			+ 1) y			+						dx =	∫	4(x			+ 1)	+			dx =
= ∫ (x			+ 1) y			+						dx =	∫	4(x			+ 1)	+			dx =
0								3				0	0							3
				4		2			19				x3				19x		4
				4		2			19				x3				19x		4
	= 4			∫0	x		+				dx = 4				+				=
	= 4				x		+				dx = 4				+				=
									3					3			3		0
																		= 4				64	+	76	=	560	.


																						3		3		3

Рис. 4.1

Рис. 4.2

Пример 4.2. Вычислить объем тела, ограниченного плоскостями z = 0, y + z = 2 и цилиндром y = x2 (рис. 4.2).

Решение.

Данное

тело

сверху

ограничено

плоскостью

z = 2 − y, поэтому

V = ∫∫(2 − y)dxdy.

Область σ есть параболический сегмент, ограниченный в плос-

кости

xOy прямой

y = 2 и параболой

y = x2. Спроектируем об-

ласть σ на ось Oy.

Тогда, с учетом симметрии тела относительно

плоскости yOz, получим

= ∫dy ∫ (2 − y)dx = ∫(2 − y)x

dy =

= ∫(2

3/2

5/2

y − y y )dy =

−

= 4 2

−

= 8 2

16 2

откуда V = 32

2 / 15.

Пример 4.3. Вычислить объем тела,

ограниченного плоскостью z = 0 и пара-

болоидом z = 3 − x2

− y2

(рис. 4.3).

Решение. Сверху данное тело ограни-

чено

параболоидом z = 3 − x2

− y

2 ,

по-

этому

V = ∫∫(3 − x2 − y2 )dxdy.

Область σ есть круг; уравнение получаем подстановкой z = 0 в уравнение

z = 3	2	2	.	Рис. 4.3
z = 3	− x	− y	.

В полярных координатах уравнение этой окружности имеет вид ρ2 = 3, или ρ = 3.

Учитывая симметрию тела относительно плоскостей xOz, yOz, найдем

	V		π/2	3	1	π/2	(3 − ρ2 )2		3
			π/2	3		π/2
		=	∫ dϕ ∫ (3 − ρ2 )ρdρ = −			∫			dϕ =
4		=	∫ dϕ ∫ (3 − ρ2 )ρdρ = −		2	∫	2		dϕ =
4			0	0	2	0	2		0
			0	0		0			0
										9	π/2	9		π/2	9π
											π/2			π/2
								=			∫ dϕ =		ϕ	=		,
								=			∫ dϕ =		ϕ	=		,
								4			0	4		0	8
											0			0

откуда V = 9π / 2.

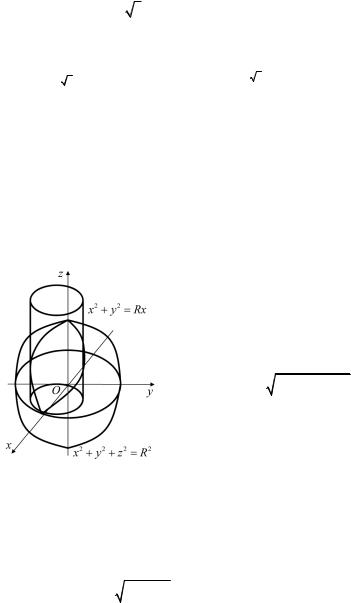
Пример 4.4. Вычислить объем тела, вырезанного цилиндром x2 + y2 = Rx из сферы x2 + y2 + z2 = R2 (рис. 4.4).

Решение. Рассматриваемое тело симметрично относительно плоскости xOy. Рассмотрим ту его половину, которая расположена над плоскостью xOy. Сверху она ограничена сферой

x2 + y2 + z2 = R2. Поэтому

V = 2∫∫	R2 − x2 − y2 dxdy.
σ
Область σ	есть круг, ограничен-

ный окружностью x2 + y2 = Rx. Вве-

дем полярные координаты. Уравнение Рис. 4.4 окружности примет вид ρ2 = Rρcosϕ

или ρ = Rcosϕ. Так как тело симметрично и относительно плоско-

сти xOz,			достаточно вычислить объем его четверти, расположен-
ной в первом октанте:
	V		π/2	Rcosϕ	1	π/2	2(R	2	2	)	3/2	Rcosϕ

		=	∫ dϕ	∫ R2 − ρ2 ρdρ = −		∫		− ρ				dϕ =
4					2			3
			0	0		0						0

π/2

= −

∫ (sin3ϕ −1)dϕ =

∫ (1 − cos2ϕ)d cos ϕ +

π/2

cos

3ϕ

π/2

∫ dϕ =

cos ϕ −

= −

2R3

πR3

3π − 4

R3 ,

откуда V = 2(3π − 4) / 9R3.

Задача 4.1. Вычислить объемы тел, ограниченных поверхностями:

а) цилиндром x2 + y2 = a2 и плоскостями x + y + z = 2a, z = 0;

б) эллиптическим параболоидом		x2			y2
	z =			+			и плоскостями
		a	2		b	2

x = ±1, y = ±1;

		2		2
в) плоскостями y + z = 0, z = 0 и цилиндром	x		+	y	;
в) плоскостями y + z = 0, z = 0 и цилиндром	a	2	+	2	;
	a			b

г) параболоидом z = x2 + y2 +1 и плоскостями x = 4, y = 4.

5. ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПОВЕРХНОСТИ

Пусть поверхность задана уравнением z = f (x, y)

руется на плоскость xOy в область σ. Тогда ее площадь по формуле

S = ∫∫			∂z 2	∂z		2
	1	+		+		dxdy.

			∂x		∂y

и проекти-

S находят

(5.1)

Пример 5.1. Вычислить площадь части поверхности цилиндра z2 = 4x, лежащей в первом октанте, вырезанной цилиндром y2 = 4x и плоскостью x = 1.

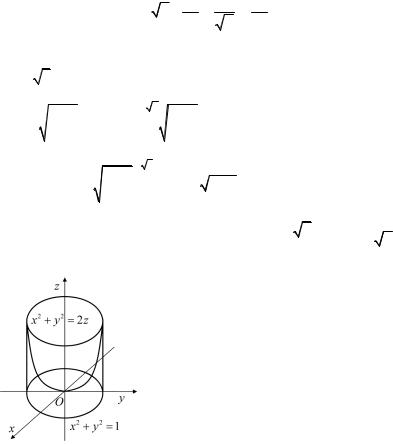
Решение. Из уравнения поверхности z2 = 4x для первого октанта имеем

z = 2 x; ∂z = 1 ; ∂z = 0.
∂x	x ∂y

Область σ ограничена в плоскости xOy параболой 4x = y2 или

y = 2

x, прямой x = 1 и осью Ox. Поэтому

S = ∫∫

dxdy =

∫dx

∫

dy =

= ∫ y 1+

dx = 2∫ x +1dx =

(x +1)3/2

8 2

−

(2 2 −1).

Пример 5.2. Вычислить площадь части

поверхности

параболоида

2z = x2 + y2 ,

вырезанной

цилиндром

x2 + y2 = 1

(рис. 5.1).

Решение. Из уравнения параболоида

находим

z =

x2 + y2

;

∂z

= x;

∂z

= y.

∂x

∂y

Рис. 5.1

Область

σ есть

круг

с границей

x2 + y2 = 1.

Введем полярные координаты. С учетом того, что поверхность симметрична относительно координатных плоскостей xOz, yOz и что уравнение окружности, ограничивающей область σ, в полярных координатах имеет вид ρ2 = 1, или ρ = 1, получим

S		π/2	1	2		1	π/2	2		3/2	1

	=	∫ dϕ∫ρ 1 + ρ			dρ =		∫ (1 + ρ		)		dϕ =
4						3
		0	0				0				0

		π/2			π/2

	2 2 −1		2 2 −1			2 2 −1
=		∫ dϕ =		ϕ	=		π,

3		0	3		6
					0

и S = 2(2 2 −1) / 3π.

Пример 5.3. Вычислить площадь части поверхности сферы x2 + y2 +

+ z2 = a2 , вырезанной		цилиндром
x2 + y2 = R2	(R ≤ a) (рис. 5.2).
Решение.	Данная	поверхность

симметрична относительно всех трех координатных плоскостей. Для восьмой части данной поверхности, лежащей в первом октанте, имеем:

z =

;

Рис. 5.2

− x

− y

∂z

= −

∂z

−

;

∂x

∂y

− x

− y

− x

− y

Область σ есть круг с границей x2 + y2

= R2. Тогда

= a ∫∫

dxdy

− x

− y

σ/4

Введем полярные координаты. С учетом того что уравнение окружности, ограничивающей область σ, в полярных координатах

имеет вид ρ2		= R2	или ρ = R, получим
	S	π/2	R	ρdρ		a	π/2	R
		= a ∫ dϕ∫			= −		∫ 2 a2 − ρ2	dϕ =

8		0	0 a2 − ρ2		2		0	0

π/2

= −a( a2 − R2 − a)ϕ

откуда S = aπ(a − a2 − R2 ).

= aπ (a − a2 − R2 ), 2

Задача 5.1. Найти часть поверхности сферы x2 + y2 + z2 = 100,

заключенную между плоскостями x = −8, x = 6.
Задача 5.2. Вычислить		часть		поверхности			эллипсоида
x2 + y2 + z2 / 4 = 1, вырезанную цилиндром x2 + y2 = 1 / 4.
Задача 5.3. Найти	площадь части				поверхности			сферы
x2 + y2 + z2 = R2 , заключенной			между плоскостями				x = ±R / 2,
y = ±R / 2.
Задача 5.4. Найти площадь части цилиндра x2 + y2							= R2 , отсе-
каемой плоскостями z = 0, z = kx.
Задача 5.5. Найти	площадь		части	поверхности		z =		x2 + y2 ,
заключенной внутри цилиндра x			2 + y2 = 2x.
Задача 5.6. Вычислить		площадь		той	части	поверхности

z2 = 2xy, которая находится над прямоугольником, лежащим в плоскости xOy и ограниченным прямыми x = 0, x = 3, y = 0, y = 6.

Задача 5.7. Найти площадь части плоскости x / a + y / b + z / c = 1, заключенную между координатными плоско-

стями.

Задача 5.8. Найти площадь части поверхности конуса z2 = x2 + y2 , лежащей над плоскостью xOy и отрезанной плоско-

стью		(		)
стью	z = 2		x / 2	+1 .

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.02.201584.84 Кб15b1.docx
#
09.02.2015193.79 Кб33b3.docx
#
09.02.201566.29 Кб12b4.docx
#
16.09.2019359.94 Кб8basis_radiolocation.doc
#
05.09.201918.9 Mб1Bazy_dannykh_DZ.docx
#
23.03.20164.48 Mб100Bezverkhniy_Kratnye_integraly_2014.pdf
#
10.02.2015548.75 Кб10bilety.pdf
#
09.02.201589.6 Кб13Bilety_2014_Specialist.doc
#
23.09.2019826.88 Кб1Bilety_Eakhdp прошлого года такие же.doc
#
09.02.201550.83 Кб102Bilety_OP.docx
#
20.04.20195 Mб4Bilety_po_analu.doc