
Методы оценивания параметров источников сигналов АР
.pdf
уменьшающаяся с ростом п регулярная ошибка, которая ухудшает разрешающую способность характеристики ηn (ϕ) по сравнению с ηс.в. (ϕ) .
Из (2.92) непосредственно следует, что оценка пространственного спектра по методу “теплового шума” имеет более высокую разрешающую способность, чем оценка по методу Кейпона. Эти характеристики отличаются различной ошибкой αn (ϕ) и,
следовательно, различной степенью приближения к оценке пространственного спектра по методу собственных векторов. Такая общая трактовка методов Кейпона (п=1), “теплового шума” (n=2) и предложенного в [27] более общего метода (n>2) позволяет рассматривать спектральные оценки ηn (ϕ) при различных п как результат единого преобразования,
выделяющего характеристику ηс.в. (ϕ) с различной степенью точности.
Рис. 2.15 демонстрирует разрешающую способность функции ηn (ϕ) при различных значениях n=1, 2, 3, 5 и 7. В этом примере пять близко расположенных источников одинаковой мощности (ОСШ равно 20 дБ в одном элементе АР) пеленговались с помощью 16-элементной эквидистантной АР с полуволновым расстоянием между элементами. Стрелками указаны направления прихода сигналов каждого источника. Видно, что при n=7 источники могут быть разрешены, в то время как методы Кейпона (n=1) и “теплового шума” (n=2) не могут обеспечить угловое разрешение источников.
Рис. 2.15 Функции ηn (ϕ) при различных значениях n=1, 2, 3, 5 и 7. Стрелки показывают угловое положение источников сигналов.
Интересно получить аналитические выражения для разрешающей способности. Такие результаты удается получить для методов Кейпона и “теплового шума” в предположении, что в пространстве имеются два источника одинаковой мощности [27, 28]. Будем считать
61
источники излучения разрешенными в том случае, если адаптивная характеристика ηn (ϕ)
формирует отдельный максимум в каждом из направлений φ1 и φ2. Очевидно, что если источники имеют одинаковую мощность, то эти максимумы равны, то есть
ηn (ϕ1 ) =ηn (ϕ2 ) . Следовательно, критерий разрешения для двух одинаковых по мощности
источников можно представить в виде
η2 (ϕ0 ) < η1 (ϕ1 ), |
(2.95) |
где φ0 - координата среднего направления ϕ0 = (ϕ1 +ϕ2 ) 2 |
между рассматриваемыми |
источниками. |
|
Согласно этому критерию для методов Кейпона можно получить следующее
выражение, для оценки пределов относительного углового разрешения |
|
|||||||
ϕ |
|
-ϕ |
æ |
- 3,125 + |
|
ö1 2 |
|
|
|
1,082νN +1,573 |
, |
(2.96) |
|||||
|
2 |
1 |
» ç |
|
|
÷ |
||
|
Dϕ |
ç |
0,427νN - 3,231 |
÷ |
|
|
||
|
è |
ø |
|
|
||||
где φ – ширина главного луча АР по уровню половинной мощности, ν – ОСШ в одном элементе АР для одного источника.
В предельном случае νN>>1 (2.96) переходит в более простую формулу |
|
||
(ϕ |
2 |
-ϕ ) Dϕ » 1,55(νN )−1 4 . |
(2.97) |
|
1 |
|
|
Для метода “теплового шума” в случае νN>>1 получается следующий результат |
|
||
(ϕ |
2 |
-ϕ ) Dϕ »1,3(νN )−1 3 . |
(2.98) |
|
1 |
|
|
Таким образом, при vN>>1 разрешающая способность метода «теплового шума» в
» 1,2(νN )1 12 раз выше, чем метода Кейпона. Например, если v=10 и N=10, то это различие составляет 1,76 раза.
12 раз выше, чем метода Кейпона. Например, если v=10 и N=10, то это различие составляет 1,76 раза.
На рис. 2.16 приведены зависимости величины (ϕ2 -ϕ1 )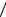 Dϕ для методов Кейпона и
Dϕ для методов Кейпона и
«теплового шума», полученные как с помощью аналитических формул (2.97) и (2.98), так и более точным численным методом. Число элементов АР N=10, а период составляет половину длины волны. Из рисунка видно хорошее соответствие в области vN>>1
приближенных теоретических оценок разрешающей способности с соответствующими численными оценками.
62
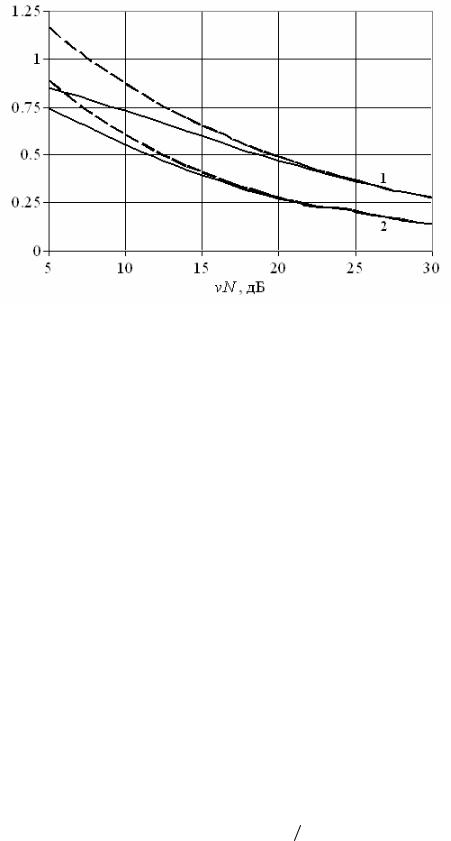
Рис. 2.16 Минимальное угловое расстояние между двумя разрешаемыми источниками одинаковой мощности v для методов Кейпона (кривые 1) и теплового шума (кривые 2). Сплошные кривые соответствуют моделированию, а пунктирные - аналитическим формулам
Представляет интерес также анализ устойчивости обобщенного метода сверхразрешения к влиянию случайных ошибок, возникающих вследствие конечного числа отсчетов вектора входных колебаний при оценке КМ М. В реальных системах
оценка КМ формируется максимально правдоподобно по конечному числу статистически независимых отсчетов вектора входного сигнала Z.
Такая оценка дается формулой (см., например, [2-8])
) |
1 |
L |
|
|
M = |
åΖ j ΖHj . |
(2.99) |
||
|
||||
|
L j=1 |
|
||
Численные результаты для разрешающей способности в случае двух источников одинаковой мощности и параметра n=1, 2, 3, 5, 7 сведены в табл.2.1. При моделировании число отсчетов L при оценке КМ выбиралось равным 500. Рассматривалась 10-элементная АР (N=10) с полуволновым межэлементным расстоянием (d/λ=0.5). Полученная
разрешающая способность выражена в единицах ширины луча АР по уровню половинной мощности и усреднена по десяти реализациям.
Таблица 2.1.
ОСШ(дБ) |
|
|
(ϕ2 −ϕ1 ) |
ϕ |
|
|
|
|
|
|
|
|
n=1 |
n=2 |
n=3 |
n=5 |
n=7 |
|
|
|
|
|
|
-10 |
0,920 |
0,864 |
0,812 |
0,726 |
0,662 |
0 |
0,691 |
0,532 |
0,438 |
0,357 |
0,334 |
63
10 |
0,435 |
0,269 |
0,209 |
0,181 |
0,176 |
20 |
0,255 |
0,134 |
0,109 |
0,099 |
0,099 |
30 |
0,145 |
0,071 |
0,058 |
0,056 |
0,054 |
|
|
|
|
|
|
Анализируя приведенные в таблице результаты, можно убедиться, что разрешающая способность АР возрастает как с увеличением ОСШ, так и с увеличением степени n обратной КМ.
Теоретический анализ флуктуаций разрешающей характеристики ηn (ϕ) выполнялся в работе [28]. Было установлено, что из-за неточного задания КМ входных сигналов дисперсия функции, обратной к разрешающей характеристики ηn (ϕ) , равна
< (ξ)(n) -ξ (n) )2 >= |
n2 |
(ξ (n) )2 , |
(2.100) |
|
L |
||||
|
|
|
где ξ (n) = [ηn (ϕ)]−1 , L- число выборок в (2.99), n – степень обратной КМ.
Физический смысл (2.100) заключается в том, что дисперсия флуктуации адаптивной оценки пространственного спектра будет возрастать при уменьшении числа отсчетов L, а
улучшение разрешающей способности путем увеличения степени п требует соответствующего повышения точности оценки КМ М (L~n2).
2.4 Проекционный метод углового разрешения источников сигналов
Обобщение метода Кейпона показало, что с ростом степени n разрешающая
способность |
адаптивной АР с выходной характеристикой ηn (ϕ) |
(2.91.2) |
монотонно |
||||
возрастает, |
а сама разрешающая |
функция ηn (ϕ) |
при |
неограниченном |
|
увеличении |
|
|
|
−1 |
|
æ |
J |
ö |
|
параметра n стремиться к величине |
[SH (ϕ)DS(ϕ)] , |
где |
D = çΕ - åUk UkH ÷ |
- матрица |
|||
|
|
|
|
è |
k =1 |
ø |
|
проектирования на шумовое подпространство. Такой метод можно назвать проекционным и обозначить разрешающую функцию как η∞ (ϕ) .
Чтобы воспользоваться этим методом, надо уметь оценивать размерность шумового подпространства и строить проекционную матрицу, используя входные сигналы. Оценивание размерности шумового подпространства равносильно оцениванию числа J внешних сигналов, принимаемых АР, поскольку размерность шумового подпространства равна N-J. Нетрудно понять, что это обстоятельство принципиально отличает проекционный метод от методов Кейпона и “теплового шума”, где размерность шумового подпространства не оценивается.
64
Пусть N-элементная АР произвольной геометрии принимает сигналы от J источников с угловыми координатами φ1, φ2,…, φJ и мощностями v1,v2,..., vJ, а также аддитивные собственные шумы приемных каналов. Проекционный метод можно использовать только в случае, когда число источников меньше числа приемных каналов АР (J<N). Будем также считать, что сигналы и аддитивные шумы представляют собой случайные, нормально распределенные комплексные величины с нулевым средним значением.
1. Рассмотрим вначале идеальный случай, когда число выборок бесконечно (L→ ), то есть, известна точная КМ M входного процесса. Векторное N-мерное пространство разбивается на два подпространства: сигнальное и шумовое. Первое из них имеет размерность J и соответствует сигнальным собственным числам КМ (μ1 ≥μ2 ≥ … ≥μJ ≥1). Второе подпространство является ортогональным первому, имеет размерность N-J и соответствует шумовым собственным числам КМ (μJ+1=μJ+2= … =μN =1).
КМ, как и раньше, можно представить в виде разложения (2.44) по собственным векторам Uk (k=1,2,...,N). Так как эта матрица имеет кратные собственные числа, то (2.44)
удобнее представить в другом эквивалентном виде
N′ |
|
M = åμk Пk , |
(2.101) |
k =1 |
|
где Πk - матрица-проектор на собственное подпространство, |
соответствующее |
собственному числу μk; N′ - число неравных между собой собственных чисел (N′≤J+1).
Число неравных между собой собственных чисел N′ равно степени минимального многочлена КМ M. Минимальным многочленом матрицы называют многочлен минимальной степени с коэффициентом при старшем члене, равным единице, который является делителем характеристического многочлена [31]. Это значит, что собственные числа матрицы являются простыми корнями минимального многочлена. Таким образом,
минимальный многочлен можно записать в виде |
|
ψ (μ) = (μ − μ1 )(μ − μ2 )...(μ − μN′ ). |
(2.102) |
Минимальный многочлен матрицы обладает следующим интересным свойством. Он аннулирует собственную матрицу, т.е. матрица ψ (Μ) является нулевой матрицей. Чтобы доказать этот факт, подставим в (2.102) в качестве аргумента матрицу M, и тогда мы
получаем следующее выражение |
|
ψ (M) = (M − μ1E)(M − μ2E)...(M − μN ′E) |
(2.103) |
65
Первый сомножитель (M - m1E) способен аннулировать (занулить) любые векторы первого собственного подпространства. Это значит, что любой вектор из этого собственного подпространства будучи умноженным на матрицу (M - m1E) дает нулевой вектор. Поскольку в (2.103) присутствуют все N¢ сомножителей, то матрица ψ (M)
аннулирует любой вектор N-мерного пространства. Это возможно только тогда, когда y (M) = [0].
Если в (2.103) уменьшить число сомножителей до N² (N²<N¢ ), то получим ненулевую матрицу: y0(М)¹[0]. Эта матрица будет аннулировать любой вектор Φ0, который принадлежит совокупности выбранных собственных подпространств, т.е. y0(М)Φ0=[0]. В частности, если исключить из (2.103) только один i-ый сомножитель, то получим матрицу
y N(i¢)-1 (M) , которая будет проектировать любой вектор на i-oe собственное подпространство. Таким образом, можно построить входящие в (2.101) матрицы-
проекторы Πk (k=1, 2, ..., N¢) в виде матричных многочленов
Пk |
é |
N¢ |
ùé |
N ¢ |
ù |
-1 |
(2.104) |
= ê |
∏(M - m pE)úê |
∏(mk |
- m p )ú |
. |
|||
|
ëp=1, p¹k |
ûëp=1, p¹k |
û |
|
|
||
Свойства матриц-проекторов такого типа можно найти в [3]. Отметим, что соответствующее k-му подпространству собственное число матрицы Πk равно единице, а
ееостальные (N¢-1) собственных чисел равны нулю.
Построение матриц-проекторов Πk (k=1,2,..., N¢) в принципе решает поставленные
выше задачи обработки сигналов. При этом важную роль играет матрица-проектор Πnoise
на шумовое подпространство, которую можно получить из (2.104), полагая k=N¢ и mN′ =1.
В результате будем иметь
Пnoise |
= êé∏N ¢-1 (M - m p E)úêùé∏N ¢-1 (1- m p )úù-1 . |
(2.105) |
||
|
ë p=1 |
ûë p=1 |
û |
|
В этом выражении матрица проектирования на шумовое подпространство выражена через КМ и ее собственные числа. Таким образом, мы избежали сложную с вычислительной точки зрения процедуру вычисления собственных векторов КМ.
Теперь, зная матрицу проектирования на шумовое подпространство, можно определить
число источников по формуле
J = N − Sp ( Π noise ) , |
(2.106) |
66
где Sp(.) – след матрицы. Значение Sp(Πnoise ) совпадает с размерностью шумового подпространства.
Направления на источники сигналов отождествляются согласно проекционному методу
с максимумами функции |
|
η∞ (ϕ) = [SH (ϕ)ΠnoiseS(ϕ)]−1 . |
(2.107) |
Выражение в квадратных скобках (2.107) имеет физический смысл части выходной мощности АР, соответствующей подпространству собственного шума. Если текущий угол φ у вектора S(φ) совпадает с направлением на любой источник сигнала (φ1, φ2, …, φJ), то этот вектор будет принадлежать сигнальному подпространству, а его проекция на шумовое подпространство будет равна нулю. Поэтому в этой точке функция η∞ (ϕ) имеет особенность типа 0-1. По пикам функции η∞ (ϕ) определяются угловые положения на источники сигналов.
В случае одного источника сигналов (J=1) КМ М имеет два собственных числа μ1>1 и μ2=1. Проектор Πnoise на шумовое подпространство и функция η∞ (ϕ) будут равны
Πnoise = (M − μ1Ε)(1− μ p )−1 , |
|
|
|
(2.108) |
||
η |
∞ |
(ϕ) = (1− μ )[SH (ϕ)MS(ϕ) − μ |
]−1 |
. |
(2.109) |
|
|
1 |
1 |
|
|
||
В этом случае проекционный метод полностью эквивалентен согласованной обработке,
которая является оптимальной и сводится к измерению выходной мощности SH (ϕ)MS(ϕ)
при сканировании лучом антенны. В случае двух и более источников сигналов (J>2) метод
согласованной обработки перестает быть оптимальным и отличается от проекционного метода, который дает точные значения параметров сигналов.
2. Рассмотрим теперь случай, когда число выборок входного процесса конечно и равно L. Поэтому вместо точной КМ мы должны использовать ее максимально правдоподобную оценку M из (2.99). Элементы оценочной КМ являются случайными величинами и имеют совместное распределение плотности вероятности Уишарта [5, 6].
В силу случайного характера вероятность появления кратных собственных чисел ничтожно мала. Поэтому, при L≥N матрица M имеет N случайных положительных собственных чисел μ1>μ2>…>μN >0. Шумовое собственное число, равное единице и имеющее кратность N-J для точной КМ, расщепляется на N-J простых собственных чисел оценочной КМ M . Разброс шумовых собственных чисел возрастает с уменьшением числа выборок L. Они могут принимать значения, существенно меньшие единицы. При L<N
67
выборочная матрица M является вырожденной и имеет L положительных собственных чисел, а N-L ее собственных чисел равны нулю. Подпространство, соответствующее нулевым собственным числам, ортогонально подпространству выборочных векторов Z(l)
и называется ядром матрицы M .
Теперь многочлен (2.102) состоит из N сомножителей и имеет вид |
|
ψ (μ) = (μ - μ1 )(μ - μ2 )...(μ - μN ). |
(2.110) |
то есть является характеристическим многочленом КМ M степени N. Отсюда следует, что
ψ (M) = [0] и линейно независимыми будут N степенных матриц E, M , M2 ,..., M N −1 .
Таким образом, при переходе от точной КМ М к ее оценке M число линейно независимых матриц увеличивается от N′ до N. Это обусловлено влиянием собственного шума и появлением множества шумовых собственных чисел вместо одного. Поэтому для оценки числа и параметров источников сигналов нельзя использовать выражения (2.105)- (2.107), основанные на проекционных матрицах (2.104), а необходимо сначала оценить степень минимального многочлена КМ M .
Для оценки степени минимального многочлена в [26] предложено использовать
статистику вида
I (m) = min |
|
|
|
) |
|
|
2 |
, |
|
|
|
I(m) (M) |
|
|
|
||
bn |
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
m |
) |
|
I(m) (M) = E - åbnMn . |
(2.111) |
||
n=1
Степень минимального многочлена находится из решения пороговой задачи с использованием априорной информации о статистических свойствах собственного шума. Если собственный шум имеет единичную КМ, то априори можно утверждать, что при отсутствии внешних сигналов степень минимального многочлена N′=1. Полагая в (2.111) m=1 и считая, что в (2.99) выборки берутся только из собственного шума, в [26] найдены среднее (<I(1)>) и дисперсия σ12 для статистики I(1) в виде
< I (1) >= |
N 2 -1 |
, |
σ 2 |
= 2 |
N 2 -1 |
é1+ |
(2N 2 - 3) |
ù . |
(2.112) |
|
|
|
2 |
|
|||||||
|
N + L |
1 |
|
(N + L) |
ê |
NL |
ú |
|
||
|
|
|
|
ë |
û |
|
||||
С помощью (2.112) определяется порог ρtarget, который можно принять равным, например, ρtarget =<I(1)> или ρtarget =<I(1)> +σ1. Величина порога зависит от числа выборок L и числа N элементов АР. При L®¥ значение ρtarget®0.
При наличии не только собственного шума, но и сигналов, статистика I(1) будет превышать значение порога. Так как с ростом m от 1 до N функционал (2.111) убывает до нуля, то всегда существует такое значение m = N¢ , при котором I(m)<ρtarget. Оценка N ¢
68
принимается за оценку степени минимального многочлена, так как дальнейшее уменьшение I(т) будет обусловлено влиянием шумовых собственных чисел. Получаемая при этом матрица I(m) (M) будет наиболее близкой к нулевой матрице.
Теперь используя оценку степени минимального многочлена можно построить
алгоритм для оценки числа источников сигналов и их параметров. Матрица I(m) (M)
представляет собой матричный многочлен степени т. Соответствующий ему
алгебраический многочлен имеет вид
m |
m |
|
ψ (m) (μ) = 1- åbn μ n = Õ(1-ζ n μ), |
(2.113) |
|
n=1 |
n=1 |
|
где ζn – величина, обратная корню многочлена ψ(m)(μ).
Многочлен такого типа получается из минимального многочлена (2.102) путем его деления на не равное нулю число (-l)nμ1μ2 … μm. В соответствии с (2.113) статистику
(2.111) запишем в другом виде |
|
|
|
|
|
|
|||
I (m) = min |
|
) |
|
2 |
, |
) |
m |
) |
(2.114) |
|
I(m) (M) |
|
|
I(m) (M) = Õ(E -ζ nM), |
|||||
ζ n |
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
где минимизация I(m) достигается за счет выбора чисел ζn. |
|
|
|
||||||
Аналогично (2.103) матрица I(m) (M) |
|
имеет ряд сомножителей и будет аннулировать |
|||||||
любой вектор при m=N, так как I(N ) (M) = [0]. При m<N векторы будут аннулироваться в некоторую сферу минимального размера. Минимальными будут и значения собственных чисел матрицы I(m) (M) , так как критерий (2.114) можно записать в виде
|
N |
m |
|
I (m) = minåÕ(1-ζ nμi )2 . |
(2.115) |
||
ζ n |
i=1 n=1 |
|
|
|
|
||
Условия минимума этого функционала можно записать как |
|
||
dI (m) dζ n = 0, |
n = 0,1, 2,...,m . |
(2.116) |
|
Отсюда получим следующую систему нелинейных уравнений для коэффициентов ζn
(n=1,2,…,m) [26]:
ζ n |
é |
m |
) |
) 2 |
ùì |
é |
m |
) |
) 2 |
ùü |
-1 |
(2.117) |
= Spê |
ÕM(E - ζ i M) |
úíïSpê |
ÕM2 |
(E -ζ i M) |
úýï |
. |
||||||
|
ë |
i=1,i¹n |
|
|
ûî |
ë |
i=1,i¹n |
|
|
ûþ |
|
|
|
|
|
|
ï |
|
|
|
ï |
|
|
||
Эта система решается итерационным путем для каждого m. Причем m значений ζn, вычисленные для функционала I(m), являются начальными приближениями для
69
вычисления (m+1) чисел ζn для функционала I(m+1). При m=1 итераций не требуется и из
(2.117) сразу имеем, что ζ 1 = Sp(M)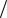 Sp(M2 ) . Практика вычислений показывает, что итерационный процесс сходится быстро. Например, достаточно не более пяти итераций, чтобы значения ζn были вычислены с точностью до 10-4 при m=4.
Sp(M2 ) . Практика вычислений показывает, что итерационный процесс сходится быстро. Например, достаточно не более пяти итераций, чтобы значения ζn были вычислены с точностью до 10-4 при m=4.
Полученный таким образом набор чисел ζn дает оценки величин, обратных собственным числам КМ М. Поэтому оценками собственных чисел будут величины ζn-1. Наименьшее из них дает оценку шумового собственного числа, а другие дают оценки сигнальных собственных чисел.
Теперь аналогично (2.104) построим оценки матриц-проекторов в виде
) |
é |
) |
) ùé |
) |
æ |
|
ζ |
öù |
-1 |
|
|
N ¢ |
N¢ |
|
|
|
|||||||
Πk |
= ê |
∏(E - M)úê |
∏ |
ç |
- |
|
p |
÷ |
|
(2.118) |
|
ζ |
|
|
|||||||||
ç1 |
÷ú . |
||||||||||
|
ë |
p=1, p¹k |
ûë |
|
è |
|
|
k øû |
|
|
|
|
|
êp=1, p¹k |
|
|
|
ú |
|
|
|||
Выражение (2.118) перейдет в (2.104) при L®¥, если учесть, что |
N ¢ ® N ¢ , M ® M , |
||||||||||
ζp®μp-1, ζk®μk-1, и сделать простые алгебраические преобразования.
Оценка проектора Πnoise на подпространство собственного шума получается при подстановке в (2.118) в качестве ζk наибольшего из полученных чисел ζn.
Теперь число действующих источников J можно оценить по формуле |
|
J = N - [Sp(Πnoise ], |
(2.119) |
где ë.û - обозначает округление до целого числа. Выражение (2.119) является аналогом точного выражения (2.106).
Угловые координаты источников сигналов будут отождествляться с максимумами функции
) |
) |
-1 |
. |
(2.120) |
η¥ |
(ϕ) = [SH (ϕ)ΠnoiseS(ϕ)] |
|||
Выражение (2.120) является аналогом точной формулы (2.107). Максимум функции η)¥ (ϕ) совпадает с минимумом функции SH (ϕ)ΠnoiseS(ϕ) . В свою очередь глубина минимума этой функции зависит от того, насколько близки к нулю сигнальные собственные числа матрицы I(m) (M) . Так как в соответствии с критерием (2.114) эта матрица выбирается наиболее близкой к нулевой матрице, то ее собственные числа будут также наиболее близки к нулю. Поэтому матрица Πnoise наиболее эффективно аннулирует векторы сигнального подпространства.
70
