
Методы оценивания параметров источников сигналов АР
.pdf
Z = a0 S(ϕ0 ) + X . |
(2.12) |
Если пренебречь влиянием шума и учесть, что SH (ϕ)S(ϕ) = S(ϕ) 2 = N , то из (2.12) и (2.11) получим следующий результат
|
S |
H |
(ϕ)Z |
2 |
|
|
a0 |
2 |
|
H |
2 |
|
a0 |
2 |
|
N |
é 2π |
|
ù |
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn (sin ϕ0 |
- sin ϕ)ú |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
= |
|
|
|
|
S (ϕ)S(ϕ0 ) |
= |
|
|
|
|
åexpê j |
|
. |
(2.13) |
|||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
S |
H |
(ϕ)S(ϕ) |
|
N |
|
|
N |
|
λ |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n 1 |
ë |
|
û |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
Нетрудно видеть, что выражение (2.13) достигает максимума при φ =φ0. Если АР эквидистантная, то xn = d(n -1) , и формула (2.13) может быть преобразована аналогично
тому, как было преобразовано выражение (1.31) в (1.35). В результате получим, что |
|
|||||||||||||
|
|
SH (ϕ)Z |
|
2 |
= |
|
a0 |
|
2 |
|
F(ϕ,ϕ0 ) |
|
2 . |
(2.14) |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
||||||||||
|
SH (ϕ)S(ϕ) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Функция F(ϕ,ϕ0 ) 2 представляет собой отклик нашего “прибора” (антенной решетки)
на плоскую волну единичной амплитуды. Ее можно назвать аппаратной функцией.
Функция F(ϕ,ϕ0 ) 2 совпадает с ДН АР по мощности. Иногда метод оценивания угла
прихода (2.11) называют методом сканирования лучом антенны.
Если сигнал отсутствует и вместо смеси Z в (2.11) входит только шум X, то средняя мощность шума на выходе равна σ2. Это мы определили ранее в подразделе 1.5.
Теперь будем полагать, что сигнал принимается на фоне шума. Тогда выход измерительной системы (2.11) представляет собой случайную функцию угловой переменной φ. Найдем среднее и среднеквадратическое отклонение этой функции. Для этого (2.12) подставим в (2.11) и найдем статистическое среднее. В результате получим,
что |
|
|
< WH (ϕ)Z 2 >= a0 |
2 F(ϕ,ϕ0 )2 +σ 2 . |
(2.15) |
Функции, рассчитанные для эквидистантной АР по формуле (2.15), и нормированные к своим максимальным значениям, представлены на рис. 2.3 (φ0=0) и рис. 2.4 (φ0=200) в
идеальном случае отсутствия шума, а также при ОСШ a0 2 /σ 2 в одном элементе АР равном 3 дБ и -3 дБ. Параметры N=16, d/λ=0.5. Во всех случаях мы наблюдаем, что максимум отклика совпадает с направлением на источник сигнала, хотя в области боковых лепестков наблюдается существенные изменения.
31

Рис. 2.3. Функция (2.15) при φ0=0 для разных ОСШ в приемной антенне, равных ∞, 3 дБ и -3 дБ, кривые 1,2,3, соответственно. N=16, d/λ=0.5
Рис. 2.4. Функция (2.15) при φ0=200 для разных ОСШ в приемной антенне, равных ∞, 3 дБ и -3 дБ, кривые 1,2,3, соответственно. N=16, d/λ=0.5
Таким образом, если в системе предусмотрено усреднение результатов измерения, то
хорошая оценка направления прихода волны может быть получена и для очень слабых сигналов. Например, в радиоастрономии для юстировки больших антенн используются достаточно слабые источники космического радиоизлучения, координаты которых известны с высокой точностью. Прием сигнала осуществляется радиометрами, которые созданы специально для приема шумовых сигналов, существенно более слабых, чем собственный шум.
32
Теперь найдем среднеквадратическое отклонение (СКО) интересующей нас функции (2.11) от ее среднего (2.15). По определению СКО равно
σ 0 |
æ |
|
W |
H |
(ϕ)Z |
|
2 |
- < |
|
W |
H |
(ϕ)Z |
|
2 |
ö |
2 |
(2.16) |
|
|
|
|
||||||||||||||
= < ç |
|
|
|
|
|
|
|
|
>÷ |
> . |
|||||||
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя сюда (2.12) и (2.15), найдем, что
σ 0 = σ 2 |
|
a |
|
2 |
|
F(ϕ,ϕ0 ) |
|
2 + σ 2 . |
(2.17) |
|
|
|
|
СКО (2.17) характеризует количественно возможные случайные отклонения отдельных реализаций отклика (2.11) от средней величины (2.15). На рис. 2.5 приведены три кривые. Под номером 1 дан средний отклик (2.15) при φ0=0 и ОСШ в одном элементе АР, равном единице (0 дБ). Кривые под номерами 2 и 3 получены путем вычитания и добавления СКО (2.17) к среднему значению (2.15). Таким образом, область отдельных реализаций отклика заключена в основном между кривыми 2 и 3. Для большей детализации кривых в области главного луча эти же результаты представлены на рис. 2.6.
Рис. 2.5. Средний отклик АР (кривая 1) и средний отклик АР с вычтенной или с добавленной СКО (кривые 2 и 3, соответственно). φ0=0, ОСШ в одном элементе АР равно 0 дБ
33

Рис. 2.6. Средний отклик АР (кривая 1). Средний отклик с вычтенной или с добавленной СКО (кривые 2 и 3, соответственно). φ0=0, ОСШ в одном элементе АР равно 0 дБ
С помощью этого рисунка оценим точность пеленгации источника излучения.
Учитывая симметрию аппаратной функции F(ϕ,ϕ0 ) 2 , направление на максимум определяют следующим образом. На уровне -3 дБ (уровень половинной мощности)
проводят прямую горизонтальную линию и находят две точки пересечения с измеренной кривой отклика прибора. Пусть координаты этих точек будут φ1 и φ2. Тогда направление на источник сигнала оценивается, как среднее арифметическое, т.е.
) |
|
ϕ |
1 |
+ϕ |
2 |
|
|
|
ϕ0 |
= |
|
|
|
. |
(2.18) |
||
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
Из рис. 2.6 видно, что координаты φ1 и φ2 являются случайными величинами. В данном примере размах относительно среднего для каждой координаты примерно равен 2σ=1,50. Считая оценки координат φ1 и φ2 статистически независимыми, находим, что среднеквадратическая ошибка пеленгации источника равна 0,530. Ширина луча равна примерно 60. Поэтому относительная погрешность пеленгации источника равна 8,9%.
После того, как получена оценка направления прихода волны ϕ)0 , можно оценить ее амплитуду. Для этого выражение (2.9) приравнивается к нулю, и оценка амплитуды а
получается в виде
) |
|
|
|
) |
|
)Z |
|
|
1 |
|
é |
2π |
) |
ù |
|
|
|
SH (ϕ |
|
|
|
N |
|
||||||||
a |
= |
|
H |
) |
0 |
) |
|
= |
|
åZn expê j |
|
xn sin ϕ |
0 ú . |
(2.19) |
|
S |
|
0 ) |
|
λ |
|||||||||||
|
|
|
(ϕ0 )S(ϕ |
|
N n=1 |
ë |
|
û |
|
||||||
Подставляя сюда Z из (2.12) и усредняя по реализациям шума, найдем среднее
значение в виде
34

) |
|
|
|
) |
) < Z > |
|
1 |
|
é |
2π |
) |
ù |
|
|
|
SH (ϕ |
|
N |
|
||||||||||
< a |
>= |
|
H |
)0 |
) |
|
= a0 |
|
åexpê j |
|
xn (sin ϕ0 |
- sin ϕ0 )ú . |
(2.20) |
|
S |
0 ) |
|
λ |
|||||||||||
|
|
|
(ϕ0 )S(ϕ |
|
N n=1 |
ë |
|
û |
|
|||||
Если выполнить также усреднение по оценкам направления на источник сигнала ϕ)0 , то мы найдем, что среднее значение оценки амплитуды равно амплитуде сигнала. Значит, оценка будет не смещенная.
2.1.2. Два дискретных источника. В этом случае сигнальная модель (2.1) должна быть
записана в виде
Z = a1 S(ϕ1 ) + a2 S(ϕ2 ) + X . |
(2.21) |
Сначала мы исследуем результат, который получается, если в данном случае применить обработку сигнала (2.11), которая является оптимальной в предположении только одного источника сигнала. Для этого рассмотрим два примера.
В первом примере мы предположим, что оба источника имеют одинаковые и равные единице амплитуды волн, т.е. а1=а2=1. Выберем два варианта направлений углов прихода: ϕ1 = -π  32, ϕ2 = π
32, ϕ2 = π 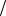 32 в первом варианте и ϕ1 = -π
32 в первом варианте и ϕ1 = -π  64, ϕ2 = π
64, ϕ2 = π 64 во втором варианте.
64 во втором варианте.
Предположим, что измерение углов прихода волн выполняется с помощью линейной эквидистантой АР из 16 элементов (N=16) и полуволновым межэлементным расстоянием (d/λ=0.5). Подставляя (2.21) в (2.11) и пренебрегая влиянием собственного шума, мы
вычислим функцию ДН АР по мощности в виде
|
|
|
|
|
|
|
|
|
SH (ϕ)[S(ϕ |
) +S(ϕ |
|
)] |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
F(ϕ) |
2 = |
|
|
1 |
|
2 |
|
|
|
. |
(2.22) |
|||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
F(ϕ) |
|
|
|
|
SH (ϕ)S(ϕ) |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Функция |
|
|
, вычисленная для первого и второго вариантов, представлена на рис. |
||||||||||||||||
|
|
||||||||||||||||||
2.7 в виде двух кривых. Мы видим, что в первом варианте (кривая 1) функция |
|
F(ϕ) |
|
|
|||||||||||||||
|
|
||||||||||||||||||
имеет два максимума, положения которых точно совпадают с направлениями прихода волн. Во втором варианте (кривая 2) наблюдается единственный максимум в направлении φ=0. В этом случае АР не может различить две волны отдельно. В чем причина такого явления?
35
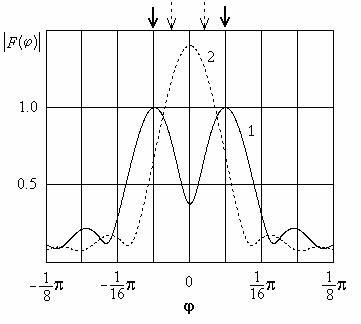
Рис. 2.7 Отклики АР в случае двух (показано стрелками) источников сигналов одинаковой мощности а1=а2=1
Чтобы ответить на этот вопрос, сравним ширину главного луча ДН нашей АР и угловое расстояние между направлениями прихода волн. Ширина главного луча ДН, вычисленная по формуле (1.38), равна π/28. Угловое расстояние между источниками в первом варианте равно π/16, а во втором варианте π/32. Следовательно, в первом случае расстояние между источниками больше ширины луча антенны, а во втором случае источники расположены на расстоянии, меньшем ширины луча. Можно предположить, что предел углового разрешения АР определяется именно шириной главного луча антенны. Это, так называемый релеевский предел разрешения.
Релей рассматривал аналогичную задачу, но в области спектрального анализа. Он
изучал возможность разрешения двух спектральных линий реальным спектральным анализатором. Отклик анализатора на одну спектральную линию называется аппаратной функцией. В нашем случае это ДН АР. Релей установил, что две спектральные линии одинаковой интенсивности могут быть разрешены, если они удалены более чем на ширину аппаратной функции. По аналогии с этим правилом мы можем сказать, что два источника одинаковой мощности могут быть разрешены, если они удалены более чем на ширину ДН антенны.
Далее мы увидим, что это правило справедливо только в случае согласованной обработки сигналов, которая определяется выражением (2.11). Эта формула была получена, исходя из априорного предположения о существовании только одного источника сигнала. В настоящее время установлено [2-9, 22, 23], что два или более
36
сигналов могут быть разрешены, даже если они находятся в пределах ширины ДН АР. Методы, которые позволяют обеспечить решение такой задачи, называются методами “сверхразрешения”. Такое название связано с тем, что эти методы превосходят предел разрешения Релея.
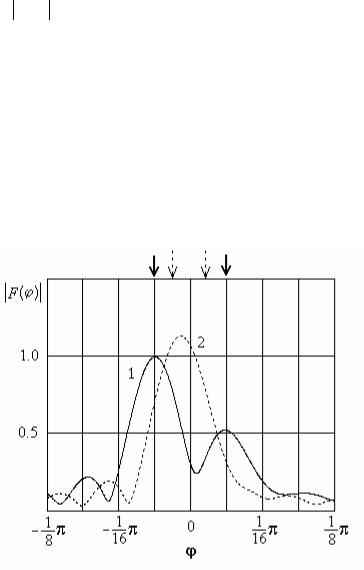
Рассмотрим также второй пример, в котором амплитуды волн различны и отличаются в два раза, т.е. а1=1; а2=0.5. Угловые положения источников такие же, как в предыдущем примере. Функция F(ϕ) , вычисленная для этого примера, представлена на рис. 2.8.
Видно, что кривая 1 имеет два максимума, как и в предыдущем примере. Направление
первого максимума совпадает с направлением на источник с большей амплитудой сигнала, в то время как направление второго максимума несколько смещено от направления на источник с меньшей амплитудой сигнала. Видно, что амплитуда второго сигнала оценивается со смещением. Это значит, что имеется систематические ошибки измерения углов прихода и амплитуд сигналов. Кривая 2 имеет один максимум, как и в предыдущем примере, но его положение смещено в сторону более мощного сигнала.
Рис. 2.8 Отклики АР в случае двух (показано стрелками) источников сигналов разной мощности
а1=1; а2=0.5
Приведенные примеры показывают, что метод измерения параметров источников сигналов в соответствии с (2.11), разработанный исходя из априорного предположения о наличии одного источника, не является оптимальным в случае двух источников сигналов.
Чтобы получить оптимальный метод измерения параметров двух сигналов, мы должны априори предположить, что в пространстве имеется два источника. Теперь в (2.21) мы имеем четыре неизвестных параметра: углы прихода двух плоских волн φ1, φ2 и их
37
амплитуды а1, а2. Если принята некоторая реализация вектора Z, то согласно методу наименьших квадратов мы должны минимизировать функцию 4-х переменных, которую
можно записать следующим образом
g(ϕ ,ϕ |
2 |
, a , a |
2 |
) = |
|
Z - a S(ϕ |
1 |
) - a |
S(ϕ |
2 |
) |
|
2 . |
(2.23) |
|
|
|||||||||||||
1 |
1 |
|
|
1 |
2 |
|
|
|
|
|
Векторы S(ϕ1) и S(ϕ2 ) образуют плоскость, если φ1≠φ2. Также мы полагаем, что число элементов решетки N>2. Поэтому вектор Z имеет размерность больше двух и представим в виде суммы двух ортогональных векторов Z11 , Z , таких, что первый лежит в плоскости векторов S(ϕ1 ),S(ϕ2 ) , а второй ортогонален ей. Аналогично (2.5) выражение (2.23) можно
переписать следующим образом
g(ϕ |
,ϕ |
2 |
, a ,a |
2 |
) = |
|
Z |
11 |
- a S(ϕ |
1 |
) - a |
S(ϕ |
2 |
) |
|
2 |
+ |
|
Z |
|
|
2 . |
(2.24) |
|
|
|
|
||||||||||||||||||||
1 |
|
1 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
Чтобы построить матрицу проектирования на заданную плоскость, векторы-столбцы
S(ϕ1 ),S(ϕ2 ) объединим в матрицу F = [S(ϕ1 ),S(ϕ2 )]. Тогда матрица проектирования на
плоскость строится следующим образом [31] |
|
Π = F(FH F)−1 FH . |
(2.25) |
Матрица ортогонального проектирования будет иметь такой вид |
|
E - Π = E - F(FH F)−1 FH |
(2.26) |
Свойства (2.7), справедливые для проекционных матриц (2.6), выполняются также и для проекционных матриц (2.25) и (2.26).
Рассмотрим более подробно проекционную матрицу (2.25). Входящую сюда матрицу
FH F представим в виде
æ |
H |
(ϕ1 ) S(ϕ1) S |
H |
(ϕ1 ) S(ϕ |
2 ) |
ö |
(2.27) |
|||||
FH F = ç S |
|
|
÷ . |
|||||||||
çSH |
(ϕ |
2 |
)S(ϕ ) SH |
(ϕ |
2 |
) S(ϕ |
2 |
)÷ |
|
|||
è |
|
|
1 |
|
|
|
|
ø |
|
|||
В случае эквидистантной линейной АР компоненты |
вектора S мы задаем |
в виде |
||||||||||
é |
2π |
|
ù |
|
|
|
|
|
|
|
|
|
Sn (ϕ1,2 ) =expê j |
|
|
d(n -1)sin ϕ1,2 ú; |
n = (1¸ N) . Отсюда |
можно |
найти компоненты |
||||||
λ |
|
|||||||||||
ë |
|
|
û |
|
|
|
|
|
|
|
|
|
матрицы (2.27). В результате будем иметь, что |
|
|
|
|
|
|||||||
|
|
H |
N |
é |
2π |
|
|
|
ù |
|
|
|
|
S |
|
|
(ϕk )S(ϕl ) =åexpê j |
|
d(n |
-1)(sin |
ϕl - sinϕk )ú; |
(k,l =1,2) . |
(2.28) |
||
|
|
|
λ |
|||||||||
|
|
|
|
n=1 |
ë |
|
|
|
û |
|
|
|
Похожее выражение встречалось в формуле (1.31). Выполняя суммирование в (2.28), получаем выражение, подобное (1.34)
38

|
|
|
|
|
|
|
é |
|
d |
|
|
|
ù |
|
|
|
|
|
|
|
|
sinêπ |
|
|
N(sin ϕl - sin ϕk )ú |
||||
|
|
|
|
|
|
|
λ |
|||||||
SH (ϕ |
|
)S(ϕ |
) = F(ϕ |
|
,ϕ |
) = |
ë |
|
|
|
|
û |
||
|
|
|
é |
|
d |
|
|
ù |
||||||
|
k |
l |
|
k |
l |
|
|
|
|
|
||||
|
|
|
|
|
|
|
sin |
êπ |
|
|
(sin ϕl |
- sin ϕk |
)ú |
|
|
|
|
|
|
|
|
λ |
|||||||
|
|
|
|
|
|
|
|
ë |
|
|
|
û |
||
é |
d |
|
|
ù |
|
|
expê jπ |
|
(N -1)(sin ϕl |
- sin ϕk |
)ú |
. (2.29) |
|
λ |
||||||
ë |
|
|
û |
|
Отсюда следует, что диагональные элементы (k=l) матрицы FH F в (2.27) равны N. Если расстояние между элементами АР выбрано так, что дифракционные лепестки
отсутствуют, |
то |
недиагональные |
элементы матрицы (2.27) меньше диагональных |
|||
элементов. В |
тех |
случаях, когда |
(sin ϕl - sin ϕk ) = |
λ |
q, (q = ±1,2,L) , недиагональные |
|
dN |
||||||
|
|
|
|
|
||
элементы равны нулю и матрица (2.27) имеет диагональный вид. В этих случаях говорят,
что векторы S(ϕ1 ),S(ϕ2 ) являются ортогональными. Математики называют матрицу (2.27)
матрицей скалярных произведений векторов или матрицей Грама. Чем больше элементов в АР, тем больше число ситуаций, когда векторы S(ϕ1 ),S(ϕ2 ) являются ортогональными.
Чтобы определить координату каждого источника, мы должны минимизировать в (2.24)
квадрат модуля ортогональной проекции Z 2 равный
|
Z |
|
2 |
= |
|
(Ε - Π)Z |
|
2 |
= |
|
Z |
|
2 - |
|
Z11 |
|
2 |
= |
|
Z |
|
2 |
- |
|
F(FH F)−1 FH Z |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
(2.30) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Угловые координаты φ1, φ2 являются независимыми переменными, и, поэтому мы должны исследовать функцию (2.30) на плоскости переменных φ1, φ2. Минимум квадрата модуля ортогональной проекции будет в точке, где максимален квадрат модуля
Z11 2 проекции, параллельной плоскости, образуемой векторами S(ϕ1 ),S(ϕ2 ) . Поэтому мы
|
|
Z11 |
|
2 |
= |
|
F(FH F)−1 FH Z |
|
2 |
|
|
|
|
|
|||||
будем исследовать величину |
|
|
|
|
. |
||||
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
Вернемся к примеру, который мы рассматривали выше. Мы предполагали, что оба источника имеют одинаковые и равные единице амплитуды волн, т.е. а1=а2=1, а углы прихода волн равны ϕ1 = π 64, ϕ2 = -π
64, ϕ2 = -π 64 . Как прежде, предположим, что измерение углов прихода волн выполняется с помощью линейной эквидистантой АР из 16 элементов
64 . Как прежде, предположим, что измерение углов прихода волн выполняется с помощью линейной эквидистантой АР из 16 элементов
(N=16) и полуволновым межэлементным расстоянием (d/λ=0.5). Метод (2.11), который мы назвали методом сканирования лучом АР, не способен был различить два сигнала (кривая 2 на рис. 2.7), так как оба источника находятся на расстоянии, меньшем ширины главного луча антенны. Теперь мы попробуем применить метод (2.30), который априори предполагает, что в пространстве имеется два источника, а неизвестными являются их угловые координаты и амплитуды волн.
39
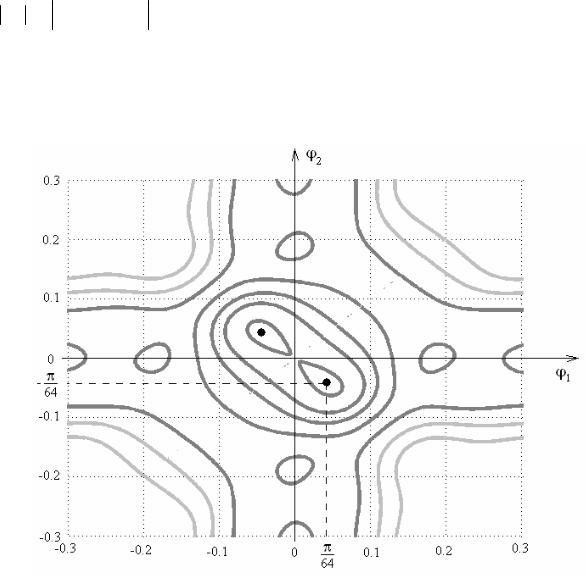
Чтобы определить угловые координаты источников, рассмотрим изолинии функции
|
|
2 |
Z11 |
2 |
= F(FH F)−1 FH Z на плоскости φ1, φ2. Напомним, что изолинией функции двух |
переменных по определению называется линия в плоскости переменных, на которой функция принимает фиксированное значение. Картина изолиний для данного примера представлена на рис. 2.9.
Рис. 2.9 Картина изолиний при разрешении двух источников одинаковой мощности а1=а2=1
Картина изолиний является симметричной относительно диагонали φ1=φ2. Это связано
с тем, что нумерация источников произвольная и функция |
|
Z11 |
|
2 |
= |
|
F(FH F)−1 FH Z |
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
симметрична относительно перестановки индексов 1 и 2. Максимум функции наблюдается в точке с координатами ϕ1 = π 64, ϕ2 = − π
64, ϕ2 = − π 64 , а также в симметричной относительно диагонали точке ϕ1 = − π
64 , а также в симметричной относительно диагонали точке ϕ1 = − π  64, ϕ2 = π
64, ϕ2 = π 64 . Таким образом, мы видим, что этот метод позволяет оценить координаты двух источников, даже если они находятся в пределах ширины главного луча АР.
64 . Таким образом, мы видим, что этот метод позволяет оценить координаты двух источников, даже если они находятся в пределах ширины главного луча АР.
Рассмотрим также второй пример, в котором амплитуды волн различны и отличаются в два раза, т.е. а1=1; а2=0.5. Угловые положения источников такие же, как в предыдущем примере. Мы видели, что источники не могут быть разрешены, если применять метод
40
