Методы оценивания параметров источников сигналов АР

Обычно используют матричную форму записи (13)

AX = B (П16)

где A={aij} – прямоугольная матрица размерности (N´M), B – вектор- столбец, состоящий из N элементов.

Имеются три основных варианта системы (15), отличающихся видом матрицы A.

а) A – квадратная матрица (M=N). Решение системы (15) зависит от того, сингулярная или не сингулярная матрица A. Если A – не сингулярная матрица, то обратная матрица A−1 существует и решение системы (П12) имеет вид

При сингулярной матрице A обратная матрица A−1 не существует и система (П15) либо не имеет решения, либо имеет множество решений.

б) A – прямоугольная матрица с числом столбцов меньшим числа строк (M<N). При этом в системе (П15) число уравнений больше числа неизвестных. Такая система называется переопределенной. Если A –матрица полного ранга rank{A} = M , то матрица

AHA является не сингулярной и для решения системы уравнений (П12) используется метод наименьших квадратов. Данный метод основан на минимизации квадрата нормы

E 2 = B - AX 2 вектора ошибки E (часто его называют вектором «невязки») между левой и правой частью в (П13). В результате последовательных преобразований получим, что

Матрица A+ = (AH A)−1 AH - называется псевдо-обратной матрицей к матрице A.

Наилучшая аппроксимация (оценка) вектора B при использовании метода наименьших

квадратов имеет вид

91

важную роль в теории адаптивной пространственной обработки сигналов. Основные свойства матрицы PA следующие. Матрица-проектор не изменяется при возведении ее в квадрат, то есть (PA)2=PA. Если некоторый вектор C принадлежит векторному подпространству, образованному векторами-столбцами Aq (q=1,2,…,M) матрицы A в (6),

то PAC = C . В противоположном случае PAC = 0. Другими словами, проекционная матрица PA проектирует любой вектор на подпространство векторов Aq матрицы A.

Минимальное значение квадрата нормы вектора ошибки E можно найти подставляя

где PA = I − PA - матрица-проектор на подпространство, ортогональное подпространству,

образованному векторами-столбцами Aq (q=1,2,…,M) матрицы A в (П6). В (П19) учтено также, что (PA )2 = PA .

Заметим, что решение по методу наименьших квадратов можно получить, умножая уравнение (П16) слева на матрицу AH . В результате получим, что AH AX = AH B . Отсюда следует формула (П19).

с) A – прямоугольная матрица, в которой число столбцов больше числа строк (M>N). В этом случае число уравнений меньше, чем неизвестных. Такая система называется недоопределённой и имеет множество решений.

Квадратичная и эрмитовая формы. Квадратичная форма реальной симметричной

или комплексной эрмитовой матрицы A соответственно равна Q(X) = XT AX и

Q(X) = XH AX . Симметричная или эрмитовая матрица A положительно определенной,

если любого вектора X величина Q(X)>0.

Собственные значения и собственные векторы. Рассмотрим характеристическое уравнение квадратной матрицы A размерности (N×N): AU=λU, где U – некоторый вектор.

Это уравнение эквивалентно системе однородных линейных уравнений (A-λI)U=0.

Поэтому матрица (A-λI) является сингулярной. Следовательно, ее определитель равен нулю: p(λ) = det(A − λ I) = 0 . Многочлен p(λ) называется характеристическим и имеет N

корней λi – собственных чисел матрицы A.

Для каждого λi матрица (A-λiI) является сингулярной и, поэтому, имеется как минимум один ненулевой собственный вектор Ui, который удовлетворяет уравнению AUi=λiUi.

92

Векторы Ui (i=1,2,…,N) можно нормировать так, что их норма Ui =1. Приведем пять свойств для собственных чисел и векторов.

1.Собственные векторы U1, U2,…, UN, соответствующие разным собственным числам линейно независимы.

2.Если rank{A} = m , то имеется (N-m) независимых решений однородного уравнения

AUi=0, которые формируют нулевое подпространство (ядро) матрицы A.

3. Собственные числа эрмитовой матрицы – действительные числа. В самом деле, из

4. Эрмитовая матрица положительно определенна, если и только, если ее собственные числа положительны. Определитель матрицы равен произведению ее собственных чисел det A = λ1λ2 KλN . Поэтому матрица A является обратимой (не сингулярной), если и только, если все собственные числа отличны от нуля.

5. Собственные векторы эрмитовой матрицы, соответствующие несовпадающим

собственным числам λi ¹ λj , ортогональны между собой ( UiH U j = 0 ). В самом деле,

умножим первое уравнение AUi = λi Ui на вектор UHj , а второе уравнение AU j = λj U j -

на вектор UiH . Затем возьмем эрмитовое сопряжение от второго уравнения и учтем, что

векторов можно обобщить на случай совпадающих собственных чисел.

Разложение квадратной матрицы по собственным векторам. Матрицу A можно представить в виде A = ULU−1 . В самом деле, набор собственных уравнений AUi=λiUi

(i=1,2,…,N) можно записать одним уравнением AU=UΛ, где не сингулярная матрица U

состоит из собственных векторов U = (U1,U2 ,K,UN ) , а диагональная матрица Λ - из собственных чисел векторов Λ = diag{λ1,λ2 ,KλN }. Умножая справа это уравнение на обратную матрицу U−1 , получим требуемое уравнение A = ULU−1 .

Учтем далее, что для эрмитовой матрицы в силу ортогональности собственных векторов UH U = IN , то есть матрица U является унитарной (UH = U−1 ) . Поэтому

93

разложение квадратной матрицы по собственным векторам можно записать двумя эквивалентными выражениями:

Отсюда следует важное свойство, которое заключается в том, что обращение эрмитовой матрицы не изменяет собственных векторов, а только трансформирует ее собственные числа (λi →1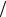λi ) .

Во многих приложениях теории ААР матрицы могут быть плохо обусловленными, что приводит к неустойчивости при их обращении. Поэтому для стабилизации обращения такой матрицы к ее диагональным элементам добавляют постоянную величину α, то есть вместо матрицы B обращают матрицу A=B+αIN . Такая операция не изменяет собственные векторы, однако смещает собственные числа. В самом деле, AUi = BUi +αUi = (λi +α)Ui ,

где λi и Ui – собственные числа и векторы матрицы B.

След матрицы A и обратной матрицы A−1 можно выразить через собственные числа следующим образом:

Часто необходимо иметь простую оценку верхней границы для максимального собственного числа λmax. Из (П22) имеем, что λmax ≤Sp{A}.

Сингулярное разложение (singular value decomposition - SVD) прямоугольной матрицы. Прямоугольную матрицу A размерности (N×M) можно представить в виде

A = UΛVH . В этом разложении Λ=diag{λ1, λ2, …, λK} – диагональная матрица ненулевых

94

V = (V1,V2 ,...,VK ) , имеющая размерность (N×K), составлена из собственных векторов матрицы HHH.

Векторы Ui и Vi образуют ортонормированные векторные системы и связаны между

95

ЛИТЕРАТУРА

1.Марков Г.Т., Сазонов Д.М. Антенны. М.: Энергия, 1975. 528 с.

2.Журавлев А. К., Лукошкин А. П., Поддубный С. С. Обработка сигналов в адаптивных антенных решетках. Л.: Изд-во Лен. универ., 1983. 240 с.

3.Караваев В.В., Сазонов В.В. Статистическая теория пассивной локации. М.: Радио и связь, 1987. 240 с.

4.Ширман Я. Д., Манжос В.Н. Теория и техника обработки радиолокационной информации на фоне помех. М.: Радио и связь, 1981. 416 с.

5.Монзинго Р.А., Миллер Т.У. Адаптивные антенные решетки: Введение в теорию. Пер. с англ. М.: Радио и связь, 1986. 448 с.

6.Уидроу Б., Стирнз С. Адаптивная обработка сигналов. Пер. с англ. М.: Радио и связь, 1989. 440 с.

7.Куликов Е.И., Трифонов А.П. Оценка параметров сигналов на фоне помех. М.: Сов.

радио, 1978. 296 с.

8.Пистолькорс А.А., Литвинов О.С. Введение в теорию адаптивных антенн. М.: Наука, 1991. 200 с.

9.Турчин В.И. Введение в современную теорию оценки параметров сигналов. Н.Новгород: ИПФ РАН, 2005.-116с.

10.Кейпон Дж. Пространственно-временной спектральный анализ с высоким разрешением // ТИИЭР. 1969. Т. 57, № 8. С. 59-69.

11.Джонсон Д. X. Применение методов спектрального оценивания к задачам определения угловых координат источников излучения // ТИИЭР. 1982. Т. 70, № 9.

С. 126-138.

12.Тихонов А.И., Арсении В.Я. Методы решения некорректных задач. М.: Наука, 1979.

288с.

13.Цейтлин Н.М. Применение методов радиоастрономии в антенной технике. М.: Советское радио, 1966. 216 с.

14.Ermolaev V.T., Gershman A.B. Fast Algorithm for Minimum-Norm Direction-of-Arrival Estimation / IEEE Trans. Signal Processing, 1994. V. 42, No. 9. P. 2389-2394.

15.Черемисин О.П. Эффективность адаптивного алгоритма с регуляризацией выборочной корреляционной матрицы // Радиотехника и электроника. 1982. Т. 27, №

10.С. 1933-1941.

96

16.Черемисин О.П. О выборе параметра для регуляризованного метода адаптивной оптимизации фильтров // Радиотехника и электроника. 1985. Т. 30, № 12. С. 23692377.

17.Абрамович Ю.И. Регуляризованный метод адаптивной оптимизации фильтров по критерию максимума отношения сигнал/помеха // Радиотехника и электроника. 1981.

Т. 26, № 3. С. 543-551.

18.Wax M., Kailath T. Detection of signal by information theoretic criteria // IEEE Trans. Acoustic, Speech, and Signal Processing. 1985. V. ASSP-33, No. 4. P. 387-392.

19.Wax M., Ziskind I. Detection of the number of coherent signal by the MDL principle // IEEE Trans. Acoustic, Speech, and Signal Processing. 1989. V. ASSP-37, No. 10. P. 11901196.

20.Lee H., Li F. An eigenvector technique for detecting the number of emitters in a Cluster // IEEE Trans. Signal Processing. 1994. V. 42, No. 9. P. 2380-2388.

21.Akaike H. A new look at the Statistical Model Identification // IEEE Trans. Autom. Control. 1974. V. AC-19, No. 6. P. 716-723.

22.Bienvenu G., Kopp L. Optimality of high resolution array processing using the eigensystem approach // IEEE Trans. Acoust., Speech, Signal Processing. 1983. V. ASSP31, No. 5. P. 1235-1248.

23.Stoica P., Nehorai A. MUSIC, maximum likelihood, and Cramer-Rao bound // IEEE Trans. Acoust., Speech., Signal Processing. 1989. V. ASSP-37, No. 5. P. 720-741.

24.Гершман А.Б. Ермолаев В.Т. Анализ собственных чисел корреляционной матрицы

входных колебаний адаптивной антенной решетки и возможности углового сверхразрешения в условиях коррелированных внешних источников // Изв. Вузов.

Радиофизика. 1988. Т. 31, № 10. С. 1236-1240.

25.Гершман А.Б. Ермолаев В.Т. Исследование проекционного метода углового разрешения на основе анализа собственных чисел корреляционной матрицы // Препринт № 272. НИРФИ. Горький. 1989. 30 с.

26.Ермолаев В.Т., Флаксман А.Г., Анурин А.А. Оценивание параметров сигналов, принимаемых антенной решеткой // Изв. Вузов. Радиофизика. 1996. Т.39, № 9. С. 1144-1160.

27.Гершман А.Б., Ермолаев В.Т., Флаксман А.Г. Адаптивное разрешение некоррелированных источников по угловой координате // Изв. Вузов. Радиофизика. 1988, Т.31, № 8. С. 941-946.

28.Гершман А.Б., Ермолаев В.Т., Флаксман А.Г. Анализ сверхразрешения некоррелированных источников излучения в адаптивных антенных решетках // Изв.

Вузов. Радиофизика. 1988, Т.31, № 11. С. 1374-1379.

97

29.Гершман А.Б., Ермолаев В.Т., Флаксман А.Г. Повышение разрешающей способности обобщенного алгоритма пеленгации Кейпона // Электромагнитные волны и электронные системы. 1997. Т. 2, № 4. С. 16-19.

30.Леховицкий Д.И., Флексер П.М., Атаманский Д.В., Кириллов И.Г. Статистический

анализ сверхразрешающих методов пеленгации источников шумовых излучений в АР при конечном объеме обучающей выборки // Сб. Антенны. 2000. Вып. 2 (45). С. 23-39.

31.Воеводин В.В. Линейная алгебра. М.: Наука, 1980. 400 с.

32.Левин Б.Р. Теоретические основы статистической радиотехники. - М.: Радио и связь, 1989. 656 с.

33.Ермолаев В.Т, Флаксман А.Г. Коррекция систематической ошибки измерения диаграммы направленности антенны, возникающей за счет угловой протяженности Солнца. Изв. Вузов. Радиофизика. 1975. Т. 18, № 3. С. 410-417.

98

ОГЛАВЛЕНИЕ

99

100