Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский государственный медицинский университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1 (производная)

.pdf

Скачиваний:

Добавлен:

19.03.2016

Размер:

951.04 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Методические рекомендации для студентов 1 курса стоматологического факультета

по самоподготовке и проведению практического занятия по математике

Тема: Нахождение производных сложных функций и производных высшего порядка. Частные производные и дифференциалы функций нескольких аргументов. Полный дифференциал функции. Использование полного дифференциала для расчета погрешностей прямых и косвенных измерений.

Актуальность темы: ознакомление с основными понятиями и методами математического анализа как средства решения задач физического, химического, биологического и иного характера, встречающихся как в процессе изучения профильных дисциплин, так и в дальнейшей профессиональной деятельности

Цель занятия: научиться вычислять частных производные, частные и полные дифференциалы сложных функций, применять полный дифференциал для обработки результатов измерений.

План изучения темы

1.Понятие производной функции в точке, ее механический и физический смысл, геометрический смысл. Связь между дифференцируемостью и непрерывностью функции.

2.Общее правило нахождения производной. Основные правила и формулы дифференцирования.

3.Производные высших порядков. Механический смысл второй производной.

4.Понятие функции многих переменных. Полные и частные приращения функций.

5.Частные производные.

6.Частные и полные дифференциалы функций многих переменных. Применение полного дифференциала для обработки результатов измерений.

Рекомендуемая литература:

Основная литература:

1. Морозов, Ю.В. Основы высшей математики и статистики: учеб. для студентов мед. и фаpмацевт. вузов и фак./Ю.В. Морозов.-

М.:Медицина, 2004.-232 с.

2. Основы высшей математики и математической статистики: учеб. для студентов мед. и фармацевт. вузов/И.В. Павлушков, Л.В.Розовский, А.Е.Капульцевич и др.-2-е изд., испр.-М.:ГОЭТАР-Медиа, 2006.-423 с.

Дополнительная литература:

1.Лобоцкая, Н.Л. Высшая математика : учеб. для вузов/ Н.Л.Лобоцкая, Ю.В.Морозов, А.А.Дунаев. – Мн. : Высш. шк., 1987. – 319 с.

2.Методические рекомендации к практическим занятиям по высшей математике [Электронный ресурс]: учеб.-метод. пособие для вузов/ авт.- сост. : Т.А.Новичкова; ГОУ ВПО "Курск. гос. мед. ун-т", каф. физики, информатики и математики.-Курск:КГМУ, 2009.

Вопросы для самоконтроля:

1.Дайте определение приращения функции, производной функции в точке.

2.Каков физический смысл производной?

3.Каков механический смысл производной?

4.В чём состоит геометрический производной?

5.Сформулируйте теорему о связи между дифференцируемостью и непрерывностью функции.

6.Назовите последовательность операций при нахождении производной по общему правилу.

7.Чему равна производная постоянной величины?

8.Чему равна производная независимой переменной?

9.Чему равна производная алгебраической суммы функций?

10.Чему равна производная произведения двух функций?

11.Чему равна производная произведения постоянной величины и функции?

	u	\|
	u	?
		?
12.Напишите формулу производной частного двух функций:	v	x
		x

13.Чему равна производная логарифмической функции?

14.Чему равна производная степенной функции?

15.Чему равна производная показательной функции?

16.Напишите формулы дифференцирования тригонометрических

	функций:	tgu \|	cosu \|
17.	sin u \|			ctgu \|		,где u=f(x).
	x	x	x		x

18.Что называется производной второго порядка (второй производной)? 19.Каков механический смысл второй производной?

20.Что называется дифференциалом функции?

21.Чему равен дифференциал функции?

22.Запишите формулу для вычисления дифференциала суммы, произведения.

23.Запишите формулу для вычисления дифференциала частного.

24.Запишите формулу для вычисления дифференциала сложной функции. 25.Что понимают под функцией двух (или нескольких) переменных?

Приведите примеры функций нескольких аргументов. 26.Напишите, что представляют собой частные и полное приращения

функции u f x, y в точке (x0, y0 ).

27.Дайте определения частных производных функции u=f(x,y) по аргументам х и у. Напишите их математические выражения.

28.Сформулируйте правило нахождения частных производных.

29.Частные производные второго порядка, формулы.

30.Как связаны частные дифференциалы и частные производные функции нескольких переменных?

31.Напишите, чему равны частные дифференциалы функции u=f(x,y)?

32.Чему равен полный дифференциал функции нескольких переменных? Напишите выражение полного дифференциала функции u=f(x,y) и

функции

Задания на

1) 5.

z=	(х х		... х	)	?
	1	2	n

самоподготовку:

Вычислить пределы:
lim	4x		2	6x 3
x 2	x		6x 8
	x	2	6x 8
		2
lim			x 4
x 4			x 4
lim		x 1 2
lim		x 5
x 5		x 5
lim		2
lim	4x		2
x	4x		2

lim	sin 4x
lim		x
x 0		x
			1	x
			1
lim 1			x
x			x

2)Найдите

1. f x, y

f x, y

частныеln y ln x

ey x2

производные следующих функций:

f f



x, y x, y



	yx		2
	yx
	2	x
	2	x
y		x
y

		f x, y
	5.	f x, y
	6.	f x, y
	6.

3) Найдите

	2		3	x

	y			8

2yx		3		2x	2	8y

полные дифференциалы следующих функций:

f x, y	1				cos 2 y

			x

	x2			y
f x, y 3					x
f x, y 2		y

Ориентировочные основы действий:

1.Изучить основные понятия по теме

2.Ответить на вопросы для самоконтроля

3.Проработать примеры решения задач по теме

4.Выполнить задания для самостоятельного контроля

5.Решить контрольные задания по теме

После изучения данной темы студент должен знать: понятие частных и полного приращений функции двух переменных,

частных производных, частных и полного дифференциалов функции многих переменных.

уметь: находить частные производные, частные и полные дифференциалы функции нескольких переменных, использовать полный дифференциал для расчета погрешностей измерений.

Краткая теория

ФУНКЦИИ ОДНОГО АРГУМЕНТА

Соответствие между двумя множествами, при котором каждому элементу x множества X по определённому закону или правилу ставится в соответствие не более одного элемента y множества Y, называется ф у н к ц и е й.

ОБОЗНАЧЕНИЕ: y = f(x)

x- независимая переменная (аргумент)

y– зависимая переменная (функция)

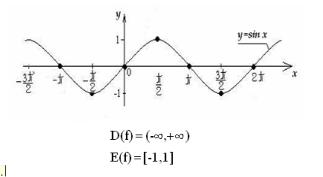
Совокупность всех значений переменной х, для которых функция y= f(x) определена, называется областью определения этой функции. ОБОЗНАЧЕНИЕ: D(f)

Совокупность всех значений переменной y называется

областью значений функции y= f(x) .

ОБОЗНАЧЕНИЕ: Е(f)

Сложной функцией называется функция, аргумент которой также является функцией, т.е. F(x)=f(φ(x))

Пример: y=sin(x3), y=ln(cos x)

Любой интервал (a,b), содержащий точку х0, называется окрестностью точки

х0.

Интервал (х0- δ, х0+ δ), где δ >0, симметричный относительно х0, называется δ -

окрестностью точки х0.

Пусть функция f(x) определена в некоторой окрестности точки х0, кроме, может быть, самой точки х0.

Число A называется пределом функции f(x) в точке х0, если для любого числа ε>0 найдется такое положительное число δ, что для любого х≠ х0, удовлетворяющего неравенству |х- х0|< δ, выполняется соотношение |f(x)-A|<

ε.

ОБОЗНАЧЕНИЕ: lim f x A
x x0
Функция называется бесконечно малой при
f x для всех x , для которых 0 x x0	.

, если

lim	f x 0
lim
x x
0

или

Свойства бесконечно малых функций.		f x при
Теорема 1(о связи бесконечно малой и предела). Если функция
x x0 имеет предел, равный числу А, то она может быть представлена в
виде f x A x ,	(1)
где x - бесконечно малая.
Справедливо и обратное: если функция f x может быть представлена
равенством (1) при x x0	, то он имеет своим пределом число А.

Теорема 2. Алгебраическая сумма конечного числа бесконечно малых в точке x0 функций есть бесконечно малая функция.

Теорема 3. Произведение ограниченной при

x x0

функции на

бесконечно малую есть бесконечно малая функция.

Следствие 1. Произведение постоянной величины на бесконечно малую есть функция бесконечно малая.

Следствие 2. Произведение конечного числа бесконечно малых функций есть функция бесконечно малая.

Основные теоремы о пределах

1. Предел суммы функций

		n				n
lim		ki			fi (x) ki lim			fi (x)
x x0 i 1						i 1	x x0
2.	Предел произведения функций
				n		n
lim			fi (x) lim fi (x)
x x0 i 1						i 1	x x0
3.	Предел частного двух функций
	f (x)				lim f (x)
lim	f (x)				x x0	, если lim g(x) 0
lim						, если lim g(x) 0
x x0	g(x)				lim g(x)		x x0
					x x0
4.	Предел сложной функции

lim		f (g(x))	f ( lim g(x))
x x	0		x x	0

5.		Предел постоянной функции

limC C

х х0

6. Первый замечательный предел

lim	sin x	1
	x
x 0

7. Второй замечательный предел

	1	x
		e
lim 1
x	x

Рассмотрим различные методы вычисления пределов.

1. подстановка

При вычислении пределов этим способом требуется подставить вместо х значение, к которому оно стремится (в данном примере это 3) и в случае если неопределенность отсутствует, то полученное значение и есть ответ.

lim	10x 4	lim	10 3 4	lim 2 2
	17		17
x 3		x 3		x 3

Остальные методы применяются, если при вычислении пределов появляются

такие ситуации как

	0
	0
	0

, называемые неопределенностями.

2. разложение на множители

При вычислении пределов этим способом требуется каждый из многочленов разложить на множители, используя формулы сокращенного умножения или вынесение общего множителя за скобки. Далее следует сократить некоторые из полученных более простых выражений и снова использовать метод подстановки.

lim	x	2	3x 2	0	lim	(x 1)(x 2)	lim	x 2	1 2	1	.


x 1 x		2	4x 5		x 1 (x 1)(x 5)		x 1	x 5	1 5	6
				0

3. умножение на сопряжённое выражение

При вычислении пределов этим способом требуется домножить либо числитель, либо знаменатель, либо обе части дроби на сопряженное выражение, т.е. то, при умножение на которое иррациональность (корень)

исчезает.				Например,			для выражения		х 3 2	сопряженным является

х 3 2			, т.к. при умножении этих выражений результирующее выражение

не будет содержать иррациональности
		2				2		2 22 х 3 4 .
	х 3				х 3		х 3

Например,

lim	x 1	lim		(x 1)( x 3 2)	lim	(x 1)( x 3 2)	lim (	x 3 2) 4.
	x 3 2		(	x 3 2)( x 3 2)		(x 3 4)
x 1		x 1			x 1		x 1

4. деление на хn

При вычислении пределов этим способом требуется разделить обе части дроби на х в наивысшей степени, если х→∞ и на х в наименьшей степени, если х→0.

В данном примере х→∞, следовательно мы должны разделить обе части

дроби на

х в наивысшей степени,

т.е.

на х

Далее используя свойства

бесконечно малых функций находят значение предела.

3x5 31x 16

165

lim 3 lim

lim

16x5

lim

1 x3 x5

x lim

lim

lim 1

x x

3 0 0 3.

0 0 1

5. использование первого замечательного предела

При вычислении пределов этим способом требуется привести предел к виду первого замечательного предела.

lim

sin 5x

lim

5 sin 5x

lim

sin 5x

x 0

5x 0

6. использование второго замечательного предела

lim 1

lim

e .

Пусть функция y f x определена на некотором интервале,

- два

произвольных значения аргумента из этого интервала.

Разность между двумя значениями аргумента называется приращением аргумента: x x0 x .

Разность между двумя значениями функции называется приращением функции: y f f x0 x f x0 .

Предел отношения приращения	y	функции	y f x	к
соответствующему приращению аргумента	x при стремлении		x к нулю и

при условии, что этот предел существует, называется производной функции в точке x :

y f x lim	y	lim	f (x x) f (x)	.
	x
x 0		x 0	x

Функция, для которой в точке х существует конечная производная называется дифференцируемой в данной точке.

Если функция имеет конечные производные во всех точках некоторого промежутка, то она называется дифференцируемой на данном промежутке.

Геометрический смысл первой производной.

Угловой коэффициент касательной, проведенной к графику дифференцируемой функции в некоторой точке, численно равен производной функции в данной точке.

(угловой коэффициент касательной = тангенсу угла наклона касательной)

Связь непрерывности и дифференцируемости

Теорема.

Если функция f(x) дифференцируема в некоторой точке х, то она непрерывна в этой точке.

Обратное утверждение неверно! Т.е. из непрерывности функции в точке не следует то, что она дифференцируема в этой точке.

Следствие.

Если функция разрывна в некоторой точке, то она не имеет производной в этой точке.

Правила дифференцирования функций

1)	(C) =0
2)	(Cu) =Cu
3)	(u+v-w) =u +v -w
4)	(uv) =u v+uv
5)	u				u v v u

					v 2
	v				v 2
6)		y		y		u		, где y=f(u), u=g(x)
			x		u		x

Таблица производных основных элементарных функций

Степенная функция

Показательная

функция

Логарифмическая

функция

Тригонометрические

функции

Обратные

тригонометрические

функции

Функция

		x
1
x
a		x
a
e	x
e
log			a	x
			a
ln x
sin x
cos x
tgx
ctgx

arcsin x

arccos x

arctgx

arcctgx

Дифференциал функции

Производная

nxn 1

	1
2	x

a		x	ln a
a			ln a
e	x
e
		1
x ln a
1
x
cos x
sin x
			1
cos				2	x
cos					x
				1
			sin		2	x
					2

			1
		1 x				2
						2
					1


			1		x2
			1		x2
			1
1 x
				2
				1

		1 x2

Согласно определению производной lim	f	f	'	x .

	x
x 0

На основании теоремы о представлении функции как суммы её предела и

б.м.ф., данное равенство означает, что f f / x x .

Умножим обе части равенства на x поучим:

f f ' x x x x ,

где α(Δх) – бесконечно малая функция при х→0.

Первое слагаемое стремится к нулю при Δx->0 медленнее второго, поэтому его называют главной частью приращения функции.

Главная часть приращения функции Δy, равная произведению y’Δx, называется дифференциалом первого порядка от функции y=f(x), соответствующим выбранным значениям x и Δx. (аналитический смысл дифференциала)

Обозначение: dy = f’(x)Δх

	x 1 x	x

Также df x f x dx , т.к. dx x

Свойства дифференциала функции

1.d C 0,C const

2.d u v du dv

3.d (u v) vdu udv

u				vdu udv
4. d
				v2
v

Формула приближённых вычислений

f (x0 x) f (x) f / (x) x

Производную f’(x) функции y = f(x) называется ПРОИЗВОДНОЙ ПЕРВОГО ПОРЯДКА или просто первой производной этой функции.

	y	dy
	y	dx
		dx

Производная функции является функцией, следовательно ее также можно дифференцировать.

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.05.20156.96 Mб49-- РаботаТимощенко 22.02.11.doc
#
23.11.2019249.08 Кб4-6.docx
#
19.03.2016951.04 Кб231 (производная).pdf
#
20.05.20151.76 Mб231 _пределы_.pdf
#
20.05.2015756.72 Кб201 Им-система-лекция 1.pdf
#
19.05.2015225.28 Кб371 ЛЕКЦИЯ .doc
#
20.05.201545.57 Кб291 модуль ПВБ.doc
#
20.05.201566.21 Кб3041-14.docx

	функций:	tgu \|	cosu \|
17.	sin u \|			ctgu \|		,где u=f(x).
	x	x	x		x