1 _пределы_

Методические рекомендации для студентов 1 курса факультета по РИУ по специальности «лечебное дело»

по самоподготовке и проведению практического занятия по математике

Тема: Основные элементарные функции и их графики. Вычисление пределов функций. Производная и дифференциал функции первого и высших порядков.

Актуальность темы: ознакомление с основными понятиями и методами математического анализа как средства решения задач физического, химического, биологического и иного характера, встречающихся как в процессе изучения профильных дисциплин, так и в дальнейшей профессиональной деятельности

Цель занятия: повторить свойства основных элементарных функций, построение графиков экспериментальных данных, научить студентов основным способам вычисления пределов, научить студентов вычислять производные и дифференциалы сложных функций одной переменной, решать физические задачи на применение дифференциала функции

План изучения темы

1.Основные элементарные функции и их графики.

2.Графическое представление экспериментальных данных.

3.Определение предела.

4.Определение бесконечно малой функции. Свойства бесконечно малых функций.

5.Основные теоремы о пределах. Методы вычисления пределов.

6.Понятие производной функции в точке, ее механический и физический смысл, геометрический смысл.

7.Связь между дифференцируемостью и непрерывностью функции.

8.Общее правило нахождения производной. Основные правила и формулы дифференцирования.

9.Производные высших порядков. Механический смысл второй производной.

10.Понятие дифференциала функции. Связь между производной и дифференциалом функции.

Рекомендуемая литература:

Основная литература:

1.Морозов, Ю.В. Основы высшей математики и статистики: учеб. для студентов мед. и фаpмацевт. вузов и фак./Ю.В. Морозов.-

М.:Медицина, 2004.-232 с.

2.Основы высшей математики и математической статистики: учеб. для студентов мед. и фармацевт. вузов/И.В. Павлушков,

Л.В.Розовский, А.Е.Капульцевич и др.-2-е изд., испр.-М.:ГОЭТАР-

Медиа, 2006.-423 с.

Дополнительная литература:

∙Методические рекомендации к практическим занятиям по высшей математике [Электронный ресурс]: учеб.-метод. пособие для вузов/ авт.-сост. : Т.А.Новичкова; ГОУ ВПО "Курск. гос. мед. ун-т", каф. физики, информатики и математики.-Курск:КГМУ, 2009.

∙Гмурман В.Е. Теория и математическая статистика. М. «Высшая школа», изд. 5, 2004.

Вопросы для самоконтроля:

1Что называется функцией?

2Что называется областью определения функции?

3Какие функции называются четными (нечетными)?

4Какие функции называются периодическими?

5Способы задания функций.

6Что называется графиком функции?

7Свойства и график степенной функции.

8Понятие и свойства обратных функций.

9Свойства и график показательной функции.

10Свойства и график логарифмической функции.

11Свойства и графики тригонометрических функций.

12Определение предела. Геометрический смысл предела

13Определение бесконечно малой величины.

14Связь бесконечно малой и бесконечно большой величин.

15Чему равен предел постоянной величины?

16Можно ли выносить константу за знак предела?

17Чему равен предел произведений нескольких функций?

18Чему равен предел частного двух функций?

19Дайте определение производной функции.

20Каков физический смысл производной?

21Каков механический смысл производной?

22В чём состоит геометрический производной?

23Сформулируйте теорему о связи между дифференцируемостью и непрерывностью функции.

24Назовите последовательность операций при нахождении производной по общему правилу.

25Чему равна производная постоянной величины?

26Чему равна производная независимой переменной?

27Чему равна производная алгебраической суммы функций?

28Чему равна производная произведения двух функций?

36Что называется производной второго порядка (второй производной)?

37Каков механический смысл второй производной?

38Что называется дифференциалом функции?

39Чему равен дифференциал функции?

40Запишите формулу для вычисления дифференциала суммы, произведения.

41Запишите формулу для вычисления дифференциала частного.

42Запищите формулу для вычисления дифференциала сложной функции.

Задания на самоподготовку:

1. Найти область определения функции y = 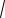9 − x 2 .

3.Построить график функций y = e x +1 и y = log 2 x .

4.Построить график функции y = -2х – 5 на интервале [5; 10].

5.Вычислить пределы:

Ориентировочные основы действий:

1.Изучить основные понятия по теме

2.Ответить на вопросы для самоконтроля

3.Проработать примеры решения задач по теме

Свойства функций и их графиков 1. Четность и нечетность

Функция называется четной, если противоположным значениям аргумента из области определения функции соответствуют равные значения функции.

f(-x)=f(x), где –x, х D(f)

График четной функции симметричен относительно оси Oy.

Примеры: y=cos x, y=x2

Функция называется нечетной, если противоположным значениям аргумента из области определения функции соответствуют

противоположные значения функции. f(-x)=-f(x), где –x, х D(f)

График четной функции симметричен относительно начала координат.

Примеры: y=sin x, y=x3

2. Периодичность

Функция f(x) называется периодической, если существует такое положительное число Т, что f (x − T ) = f (x) = f (x + T ) для любого х из области определения функции ( x − T , x, x + T D( f ))

Примеры: y=sin x, y=tg x, y= a, где а – const. 3. Ограниченность.

Функция f(x), определенная на D(f), называется ограниченной на этом множестве, если существует такое число М>0, что для всех х из D(f) выполняется неравенство

m≤f(x)≤M

График ограниченной функции лежит между прямыми y=M и y=-M.

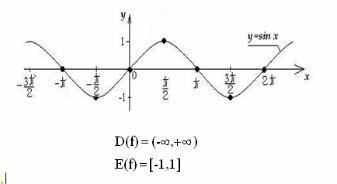
4. Монотонность

Функция y=f(x) называется возрастающей (убывающей) на интервале (a,b), если большему значению аргумента из этого интервала соответствует большее (меньшее) значение функции.

Интервал независимой переменной, в котором функция возрастает

(убывает), называется интервалом возрастания (убывания).

Интервалы возрастания, убывания называют интервалами монотонности функции, а функцию в этом интервале – монотонной функцией.

Значение аргумента, при котором функция обращается в нуль, называется

нулем функции.

Функция y=f(x) называется постоянной на интервале (a,b), если для любых х1,х2 из этого промежутка, если х1<х2, то f(x1)=f(x2).

ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ

4. Тригонометрические функции:

y=sin x, y=cos x, y=tg x, y=ctg x, y=sec x, y=cosec x 5. Обратные тригонометрические функции:

y=arcsin x, y=arccos x, y=arctg x, y=arcctg x.

Функции, полученные из вышеперечисленных с помощью

-операций сложения,

-умножения,

-вычитания,

-деления,

-операции взятия функции от функции,

применённых конечное число раз, также являются элементарными.

Сложной функцией называется функция, аргумент которой также является функцией, т.е. F(x)=f(φ(x))

Пример: y=sin(x3), y=ln(cos x)

Любой интервал (a,b), содержащий точку х0, называется окрестностью точки х0.

Интервал (х0- δ, х0+ δ), где δ >0, симметричный относительно х0, называется δ -

окрестностью точки х0.

Пусть функция f(x) определена в некоторой окрестности точки х0, кроме, может быть, самой точки х0.

limC = C

х→х0

6. Первый замечательный предел

lim sin x = 1

x →0 x

7. Второй замечательный предел

Примеры решения задач

1. Найти область определения функции f(x)= 1 - х2

х

1 - x2 ³ 0;

Решение: D( f ) =

x ¹ 0

Следовательно, D(f)=[-1;0) (0;1]

2. Установить чётность или нечётность функции

а) f(x) = х2 + cosx б) f(x) = 3x – sinx в) f(x) = lnx + 10x

Решение: а) f(-x) = (-x)2 + cos(-x) = x2 + cosx = f(x), следовательно f(x) –

чётная функция.

б) f(-x) = 3(-x) – sin(-x) = -3x + sinx = -(3x – sin x) = -f(x), следовательно f(x)

– нечётная функция.

в) – х D(f), следовательно функция не является ни чётной, ни нечётной.

3.Доказать, что функция f(x) = ex, не является периодической

Решение: Фиксируем Т>0 и находим f(x+T) = ex+T = ex·eT . Это выражение равно ex, только в случае Т=0, что противоречит определению периода функции, следовательно, f(x) - непериодическая функция.

4.Построить график функции f(x) = ex по точкам -1, 0, 1, 2, 3. Значение функции в этих точках округлить с точностью до

десятых.

Решение: Заполняем таблицу и по полученным данным строим график.