
- •Содержание
- •Введение
- •1. Понятие защищенной телекоммуникационной системы
- •1.1. Обобщенная структурно-функциональная схема ткс
- •1.2. Понятие информации
- •1.3. Понятие информационной безопасности
- •1.4. Обзор рекомендаций iso 7498-2
- •1.5. Обзор требований Руководящих документов гтк рф
- •1.6. Обзор стандарта иso/iec 15408-1-99
- •Часть 2 стандарта включает универсальный систематизированный каталог функциональных требований безопасности и предусматривает возможность их детализации и расширения по определенным правилам.
- •2. Основы криптографической защиты телекоммуникаций
- •2.1. Основы теории информации
- •Вопрос 1
- •Вопрос 2
- •2.2. Модель криптозащищенной ткс
- •2.3. Теоретическая оценка криптозащищенности ткс
- •2.4. Практическая оценка криптозащищенности ткс
- •3. Основы теории надежности
- •3.1. Основные понятия теории надежности
- •3.2. Важнейшие распределения наработки.
- •3.3. Методы статистического оценивания наработки по результатам испытаний.
- •Литература.
2. Основы криптографической защиты телекоммуникаций
Как указывалось выше, отличительной особенностью защищенной ТКС является регламентированный доступ к собственному информационному пространству. Ограничение такого доступа может осуществляться различными способами. Например, можно использовать проводные линии связи в сочетании с физической охраной протянутого кабеля (в этом отношении перспективны волоконно-оптические линии связи, позволяющие в ряде случаев исключить физическую охрану, сохраняя конфиденциальность телекоммуникаций); возможны и другие способы. Однако наиболее эффективным в плане надежности, удобства реализации, а также (в ряде случаев) стоимости является применение в ТКС криптографической защиты.
Реализация криптозащиты в ТКС на стадии проектирования, создания системы, а также ее эксплуатации всегда должна основываться на обоснованных критериях защищенности (криптостойкости). Существуют различные подходы к формированию подобного рода критериев, при этом в настоящем пособии рассматривается шенноновский подход, существенно связанный с теории информации, энтропией, позволяющий ввести и обосновать численные характеристики криптозащищенности ТКС.
2.1. Основы теории информации
Пусть имеет место некоторое случайное событие. То, что событие случайно, означает отсутствие полной уверенности в его наступлении, что, в свою очередь, создает неопределенностьв исходах опытов, связанных с данным событием. Безусловно, степень неопределенности различна для разных ситуаций. Например, если опыт состоит в определении возраста случайно выбранного студента 1-го курса дневного отделения вуза, то с большой долей уверенности можно утверждать, что он окажется менее 30 лет; хотя по положению на дневном отделении могут обучаться лица в возрасте до 35 лет, чаще всего очно учатся выпускники школ ближайших нескольких выпусков. Гораздо меньшую определенность имеет аналогичный опыт, если проверяется, будет ли возраст произвольно выбранного студента меньше 20 лет. Для практики важно иметь возможность произвести численную оценку неопределенности разных опытов.
Введение количественной меры неопределенности целесообразно начать с простой ситуации, когда опыт имеет nравновероятных исходов. Очевидно, что неопределенность каждого из них зависит отn, то есть (символически)неопределенность = f(n). Можно указать некоторые свойства функцииf:
f(1)=0, поскольку приn=1 исход опыта не является случайным и, следовательно, неопределенность отсутствует;
f(n) возрастает с ростомn, т.к. ввиду большого числа возможных исходов предсказание результата опыта становится весьма затруднительным.
Для определения явного вида функции f(n) рассмотрим два независимых опытаAиB, с количествами равновероятных исходов, соответственноnAиnB. Рассмотрим также сложный опытC, который состоит в одновременном выполнении опытовAиB. Число возможных исходов опыта С равноnAnB, причем, все они равновероятны. Очевидно, неопределенность исхода такого опыта будет больше неопределенности опытаA, поскольку к ней добавляется неопределенностьB. Естественно допустить, что мера неопределенностиCравна сумме неопределенностей опытовAиB, то есть неопределенность аддитивна:
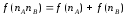 (1)
(1)
Теперь можно задуматься о том, каким может быть явный вид функции f(n), чтобы он удовлетворял приведенным выше свойствам и соотношению (1)? Легко увидеть, что такому набору свойств удовлетворяет функцияlog(n), причем можно показать, что она единственная из всех возможных классов функций. Таким образом, за меру неопределенности опыта сnравновероятными исходами можно принять числоlog(n).
Следует заметить, что выбор основания логарифма в данном случае значения не имеет, поскольку в силу известной формулы перехода от одного основания логарифма к другому logbn=logbalogan, переход к другому основанию состоит во введении одинакового для обеих частей выражения (1) постоянного множителяlogba, что равносильно изменению масштаба (то есть размера единицы) измерения неопределенности. Поскольку это так, мы имеет возможность выбрать удобное для нас (из каких-то дополнительных соображений) основание логарифма. Таким удобным основанием оказывается 2, поскольку в этом случае за единицу измерения принимается неопределенность, содержащаяся в опыте, имеющем лишь два равновероятных исхода, которые можно обозначить, например,ИСТИНА(True) иЛОЖЬ(False) и использовать для анализа таких событий аппарат математической логики.
Единица измерения неопределенности при двух возможных исходах опыта называется бит. Названиебитпроисходит от английскогоbinary digit, что в дословном переводе означает «двоичный разряд» или «двоичная единица».
Таким образом, установлен явный вид функции, описывающей неопределенность опыта, имеющего nравновероятных исхода:
 (2)
(2)
На основании формулы для равновероятных
исходов
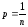 и (2) несложно найти неопределенность,
вносимую каждым отдельным исходом в
общую. Поскольку исходовnи все они равновероятны (и, следовательно,
равнозначны), а общая неопределенность
равнаlog2n,
из свойства аддитивности неопределенности
следует, что неопределенность, вносимая
одним исходом, составляет
и (2) несложно найти неопределенность,
вносимую каждым отдельным исходом в
общую. Поскольку исходовnи все они равновероятны (и, следовательно,
равнозначны), а общая неопределенность
равнаlog2n,
из свойства аддитивности неопределенности
следует, что неопределенность, вносимая
одним исходом, составляет
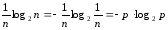 . (3)
. (3)
Таким образом, неопределенность E, вносимая каждым из равновероятных исходов, равна:
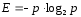 . (4)
. (4)
Обобщая формулу (4) на ситуацию, когда исходы опытов не равновероятны, например, p(A1) иp(A2), имеем:
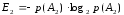 , (5)
, (5)
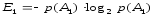 , (6)
, (6)
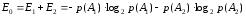 . (7)
. (7)
Обобщая это выражение на nнеравновероятных исходов, получаем:
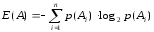 . (8)
. (8)
Введенная таким образом величина
называется энтропиейопытаA.
С учетом формулы для среднего значения
дискретных случайных величин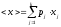 ,
можно записать (8) в виде
,
можно записать (8) в виде
 . (9)
. (9)
Это означает, что энтропия является мерой неопределенности опыта, в котором проявляются случайные события, и равна средней неопределенности всех возможных его исходов.
Из такого определения вытекают следующие свойства энтропии.
1. Как следует из (8), E=0
тогда и только тогда, когда какая-либо
из вероятностейp(Aj)=1.
Однако при этом из условия нормировки следует, что все остальные p(Ai)=0
(ij), то есть реализуется
ситуация, когда один из исходов является
достоверным (а событие перестает быть
случайным). Во всех остальных случаях,
очевидно, E > 0.
следует, что все остальные p(Ai)=0
(ij), то есть реализуется
ситуация, когда один из исходов является
достоверным (а событие перестает быть
случайным). Во всех остальных случаях,
очевидно, E > 0.
2. Из аддитивности неопределенностей следует, что и энтропия, как мера неопределенности, должна обладать аддитивностью, то есть для двух независимых опытов AиB
E(AB)=E(A)+E(B), (10),
то есть энтропия сложного опыта, состоящего из нескольких независимых, равна сумме энтропий отдельных опытов.
3. Пусть имеется два опыта с одинаковым числом исходов n, но в одном случае они равновероятны, а в другом – нет. Каково соотношение энтропий опытов? Можно доказать, что
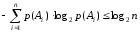 , (11)
, (11)
то есть при прочих равных условиях наибольшую энтропию имеет опыт с равновероятными исходами.Другими словами, энтропия максимальна в опытах, где все исходы равновероятны.
При этом имеет место аналогия с понятием энтропии, используемой в физике, когда энтропия выступает как мера беспорядка в системе, при этом вероятность состояния системы максимальна у полностью разупорядоченной (равновесной) системы, причем энтропия и термодинамическая вероятность связаны логарифмической зависимостью.
Рассмотрим пример. Пусть имеются два ящика, в каждом из которых по 12 шаров. В первом – 3 белых, 3 черных и 6 красных; во втором – каждого цвета по 4. Опыты состоят в вытаскивании по одному шару из каждого ящика. Что можно сказать относительно неопределенностей этих опытов? Согласно (10) находим энтропии обоих опытов:
 , (12)
, (12)
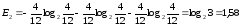 . (13)
. (13)
Отсюда видно, что E2>E1, т.е. во втором опыте неопределенность исхода выше, что, кстати, иллюстрирует справедливость формулы (11).
Энтропия E(A) в соответствии с приведенным выше определением показывает неопределенность исхода опыта A. Возможна ситуация, когда в результате некоторого опытаB, который независим отAи предшествует ему, неопределенностьAуменьшится.
Например, имеется три груза разной массы, и опыт состоит в определении наиболее тяжелого. Очевидно, неопределенность опыта уменьшится, если предварительно провести вспомогательный опыт – сравнить массы двух грузов и найти более тяжелый из них. Пусть EB(A) – энтропия нового опыта, который нужно будет произвести после опыта B. Очевидно,E(A)EB(A), причем равенство реализуется в том случае, если знание исхода опытаBникак не сказывается на неопределенности опытаA. В остальных случаях знание исхода опытаBпонижает неопределенность опытаA. РазностьE(A) и EB(A), очевидно, показывает, какие новые данные относительноAмы получаем, произведя опытB. Эта разность называетсяинформацией относительно опыта A, содержащейся в опыте B.
 (14)
(14)
Это выражение открывает возможность численного измерения количества информации. Из него легко получить ряд следствий:
поскольку единицей измерения неопределенности является бит, то в этих же единицах может быть измерено количество информации;
пусть B=A, то есть произведен опытA; очевидно, что при этом полностью снимается неопределенность исхода опытаA, то есть EA(A)=0, тогдаH=E(A) иэнтропия опыта равна информации относительно события A, которая содержится в самом опыте;
энтропия опыта равна той информации, которую мы получаем в результате его осуществления.
Последнее утверждение позволяет записать:
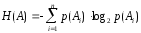 . (15)
. (15)
На основании (15) можно определить среднее количество информации, содержащейся в каком-либо исходе опытаA. Рассмотрим ряд примеров применения этой формулы.
Пример 1. Какое количество информации требуется, чтобы узнать исход броска монеты?
Решение.В данном случаеn=2 и события равновероятны, т.е.p1=p2=0,5. Согласно (15),
H= –0,5log20,5 – 0,5log20,5 = 1 бит.
Пример 2. Некто задумал целое число в интервале от 0 до 3. Наш опыт состоит в угадывании этого числа. На наши вопросы Некто может отвечать лишь «Да» или «Нет». Какое количество информации мы должны получить (сколько задать вопросов), чтобы узнать задуманное число (полностью снять начальную неопределенность).
Решение. Исходами в данном случае являются:
A1= «задуман 0»,A2= «задумано 1»,A3= «задумано 2»,A4= «задумано 3».
Предполагая, что вероятности «быть задуманными» у всех чисел одинаковы, для n=4 имеемp(Ai)=1/4,log2p(Ai)= –2 иH= 2 бит. Таким образом, для полного снятия неопределенности опыта (угадывания задуманного числа) нам необходимо 2 бит информации, то есть ответы на 2 вопроса с двумя возможными вариантами ответов (да – нет).
Количество информации равно числу вопросов с бинарными вариантами ответов, которые необходимо задать, чтобы полностью снять неопределенность задачи.
Какие вопросы необходимо задать, чтобы процесс угадывания был оптимальным, т.е. содержал минимальное их число? Здесь удобно воспользоваться так называемым выборочным каскадом (рис. 2):

