3.2. Важнейшие распределения наработки.

В теории надежности большое значение имеют некоторые теоретические распределения наработки, хорошо аппроксимирующие реальные распределения. Основные характеристики таких распределений (функция распределения, плотность, вероятность безотказной работы, математическое ожидание, дисперсия, интенсивность отказов) рассматриваются в настоящем разделе.

1. Экспоненциальное распределение.

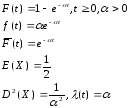
Относится к наиболее используемым распределениям, поскольку упростить исследования и вообще провести вычисления часто можно лишь для «не стареющих» систем с экспоненциально распределенной наработкой. Не подходит для моделирования сильных изменений интенсивности отказов в течение времени.

2. Распределение Вейбулла-Гнеденко.

Если случайная величина 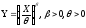экспоненциально распределена с параметром=1, то случайная величинаXимеет распределение Вейбулла-Гнеденко.

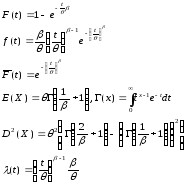
Последовательная система, образованная из независимых элементов, имеющих одинаковое распределение Вейбулла-Гнеденко, также имеет распределение Вейбулла-Гнеденко.

3. Распределение Эрланга.

В частном случае n=1 распределение Эрланга превращается в экспоненциальное распределение с параметром α.

4. Гамма распределение.

Интенсивность отказов для гамма-распределения является возрастающей при β>1 и убывающей при β<1.

5. Усеченное слева нормальное распределение.

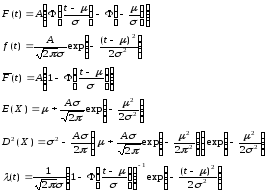
При этом обозначено 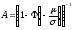. Нетрудно убедиться, что согласно такому определениюF(0)=0 иF(∞)=1, в то время как для нормально распределенной случайной величины, то есть наработка с положительной вероятностью принимает отрицательные значения. Именно поэтому нормальное распределение «усекают» слева относительно 0.

6. Логарифмически нормальное распределение.

Если величина Y=ln(X) имеет нормальное распределение с математическим ожиданием µ и дисперсией², тоXназывается логарифмически нормально распределенной случайной величиной.

Логарифмически нормальное распределение мало пригодно для описания распределения наработки, тем не менее оно используется в качестве распределения времени восстановления.

7. Обратное гауссовское распределение.

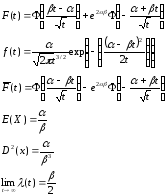
Обратное гауссовское распределение используется тогда, когда работоспособность системы зависит от нормально распределенного параметра, изменение которого во времени приводит к постепенному отказу.

3.3. Методы статистического оценивания наработки по результатам испытаний.

На практике при анализе надежности систем, вообще говоря, не знают (полностью или частично), каковы функции распределения наработок и времени восстановления. Информацию об этих распределениях получают при оценивании результатов измерения или наблюдения с помощью соответствующих статистических методов.

Основной задачей далее является аппроксимация полученного эмпирического распределения некоторым теоретическим (например, одним из рассмотренных в предыдущем разделе) с целью определения требуемых характеристик надежности анализируемой системы (например, средней наработки). Такая аппроксимация основывается на выявлении «схожести» эмпирического и одного из предлагаемых теоретических распределений при некоторых значениях параметров.

К настоящему времени разработаны несколько методов подобной аппроксимации, в основе которых лежит понятие полной выборки. Под полной(простой)выборкойпорядкаnслучайной наработкиXс функцией распределенияFпонимают случайный векторX_n*=(X₁,X₂,...,X_n), компонентыX_iкоторого являются независимыми одинаково распределенными случайными величинами с функцией распределенияF(t)=P(X_i≤t). Еслиx_i– реализация выборкиX_i, тоx_n=(x₁,x₂,...,x_n) естьреализациявыборкиX_n, иликонкретная выборкапорядкаn. Ее можно получить, если зарегистрировать наработкиnстатистически эквивалентных систем, которые работают независимо друг от друга в одинаковых условиях. Если упорядочить компоненты конкретной выборки по возрастанию, получим реализацию соответствующейупорядоченной выборки

X*_(n)=(X_(1),n, X_(2),n,..., X_(n),n), X_(i),n≤ X_(i+1),n, i=1,2,...,n-1. (75)

Пусть заданы полная выборка X_n*=(X₁,X₂,...,X_n) и соответствующая упорядоченная выборкаX*_(n)=(X_(1),n,X_(2),n,...,X_(n),n) случайной наработкиX, имеющей функцию распределенияF. Определим кусочно-постоянную функцию с помощью формулы

(76)

при этом F_n(t) называетсяэмпирической функцией распределения.

Первый вариант аппроксимации заключается в сравнении графиков эмпирической и теоретической функции распределения «на глаз». Учитывая, что наибольшая точность подобного сравнения достигается, очевидно, при сравнении двух прямых, используют соответствующее преобразование координат.

Более строго: полагая, что рассматривается двухпараметрическое семейство распределений наработки {F(t;a,b);a,b}, в общем случае графикF(t;a,b) как функции отtне позволяет сделать утверждение относительно того, к какому типу распределений принадлежит функцияF. Однако после преобразования координат, переводящего функциюF(t;a,b) в прямую, сравнительно нетрудно вынести решение о применимости или неприменимости соответствующего теоретического распределения для описания анализируемой наработки «на глаз» по визуальной близости двух прямых. При этом соответствующее преобразование координат нетрудно определить из условия

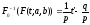. (77)

Соответствующее преобразование координат для известных теоретических распределений можно выполнить сразу при построении сетки координат в трансформированном в соответствии с (77) масштабе. Подобные координатные сетки, построенные для конкретных теоретических распределений, называются вероятностной бумагой.

В случае, когда эмпирическое распределение может быть аппроксимировано некоторым теоретическим, точки выборки, нанесенные на соответствующую вероятностную бумагу, образуют прямую.

В силу неточности подобного субъективного метода, существуют альтернативные критерии согласия теоретического и эмпирического распределений. Наиболее известным является критерий согласия ². Для применения этого критерия положительная действительная ось разбивается наkнепересекающихся интерваловI₁=[a₀,a₁),I₂=[a₁,a₂),...,I_k=[a_k-1,a_k), гдеa₀=0,a_k=∞. Также задаются вероятностиp_j,j=1,2,...,k, того, что при гипотезеH(соответствующей тождествуF=F₀, то есть согласию распределений) наработкаXлежит в интервалеI_j:p_j=F₀(a_j)-F₀(a_j-1). Идея критерия²состоит в сравнении величинnp_j(среднее число значений наработки, попавших в интервалI_jпри гипотезеH) с числом наблюденийm_j, лежащих в интервалеI_jи полученных в результате испытания,j=1,2,...,k. «Хорошее совпадение»np_jиm_jдляj=1,2,...,k, говорит против отклонения гипотезыH.

В качестве меры отклонения (расстояния) используется ²-статистика вида

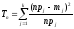. (78)

При гипотезе Hэта тестовая статистика дает приn→∞²-распределение с (k-1) степенью свободы. Соответствующий тест выглядит следующим образом:

(79)

где представляет собой табличное значение (1-α)-квантиля²-распределения с (k-1) степенью свободы.

Аналитические тесты согласия позволяют выносить более точные решения, нежели вероятностная бумага. При этом помимо критерия согласия ²существуют другие критерии (статистика Колмогорова-Смирнова, Крамера-Мизеса и другие), которые можно найти в соответствующей литературе.