Билет 1

(Понятие множества. Отношения и операции над множествами и их свойства. Булеан множества.)

1) Множества и операции над множествами

Множество - это совокупность, набор элементов, объединенных общими свойствами.

Множества обозначаются заглавными латинскими буквами A,B,C,… , а элементы множества строчными латинскими буквами a,b,c,… .

Запись A={a,b,…F(a,b,..)=0} означает, что есть множество A с элементамиa,b,… , которые связаны между собой какой-то функцией F(a,b,…)=0.

Замечание. Элементы в множество входят по одному разу, т.е. без повторений.

Основные операции:

1. Принадлежность элемента множеству:aAгде a -- элемент и A -- множество (элемент a принадлежит множеству A ).

2. Непринадлежность элемента множеству:aAгде a -- элемент и A -- множество (элемент a не принадлежит множеству A ).

3. Объединение множеств:AB .Объединением двух множествA и B называется множество C, которое состоит из элементов множеств A и B , т.е.C=AB={cA или cB}

4. Пересечение множеств:AB .Пересечением двух множествA и B называется множество C , которое состоит из общих элементов множеств A и B , т.е.C= AB ={cA и cB}

5. Разность множеств: A\B .Разностью двух множествA и B , например, множество A минус множество B , называется множество C , которое состоит из элементов множества A , которых нет в множестве B , т.е.C=A\B={cA и cB}

6. Симметрическая разность множеств: AB=(A\B)(B\A).Симметрической разностью двух множествA и B называется множество C , которое состоит из не общих элементов множеств A и B , т.е.C=AB

7. Дополнение множества:C_uA=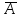.Если предположим, что множествоA является подмножеством некоторого универсального множества U , тогда определяется операция дополнения:C_uA=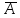=U\A={aU и aA}

8. Вхождение одного множества в другое множество: AB .Если любой элемент множества A является элементом множества B , то говорят, что множество A есть подмножество множества B (множество A входит в множество B ).

9. Не вхождение одного множества в другое множество: AB .Если существует элемент множества A , который не является элементом множества B , то говорят, что множество A не подмножество множества B (множество A не входит в множество B).

 Свойства операций над множествами:

Пусть —множество. Множество всех подмножеств множества называетсябулеаном (также степенью множества, показательным множеством или множеством частей) и обозначаетсяили. Ясно, чтои.

Число подмножеств конечного множества, состоящего из элементов равно .

Билет 2

(Индуктивный подход к построению класса всех множеств, исходя из совокупности множеств . Сложность множества. Примеры.)

Одним из наиболее методов определения объектов и совокупностей объектов назыв. Метод индуктивных определений. Предположим, что нужно построить класс объектов К для этого:

1) Опред-ся исходные объекты, без всяких доп. обоснований. То есть непосредст. указ. те объекты( своеобраз атомы, которые нужно считать принадлежащим области К.

2) Указ-ся совокупность эффект-х правил которые позвол строить из ране построенных объектов строить все более и более слож объектов совокупности К

Построение совокупности К опред по шагам. Применим этот метод для построения совокуп К всех множеств которые можно получ из исход множеств(атомов) посредством приминения к ним теоретиком нож-ых операции.

А) базис индуктивного опред-я. Всякое исход мн-во А_і(і=1,2….) (вроде спит.) множеством строящихся совокуп-тей К. Всем этим множ-ам присвое-я сложность 0.

Б) индуктивное предполож.(шаг t). Предположим, что на шагах с номерами 0,1,2,…. t уже построены все множ-ва из класса К и определенны их сложности

В)Индукционный шаг(шаг t+1) множество шага t+1 строется исходя из мно-ва предшествующих шагов посредством прим к ним(не более раза) одной из теоретиком нож-х операций

При этом сложность множ М с шагом t+1 опред. По формуле S(M)=max[S(A);S(B)]+1, где А и В множество шагов 0,1,2,… t из которых получ мн-во М посредством прим-я теорет множ операции (т.е M=AᴗB; M=AᴖB; M= B\A)

Билет 3

(Диаграммы Эйлера-Венна и их применение к обоснованию равенств «сложных» множеств. Примеры.)