1) Диаграммы Эйлера-Венна

Круги́ Э́йлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.

Важный частный случай кругов Эйлера — диаграммы Эйлера — Венна, изображающие все 2ⁿ комбинаций n свойств, то есть конечную булеву алгебру. При n=3 диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

Операции над множествами рассматриваются для получения новых множеств из уже существующих.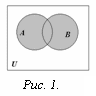

Определение. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1):

Определение. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 2):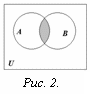

Определение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 3):

Определение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В (рис. 4):

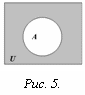
Определение. Абсолютным дополнением множества А называется множество всех тех элементов, которые не принадлежат множеству А (рис. 5):

БИЛЕТ 4

(Метод включений и его применение к доказательству равенств «сложных» множеств.)

1)Метод включений. Примеры

Формула включений-исключений(или принцип включений-исключений) — комбинаторнаяформула, позволяющая определить мощностьобъединенияконечного числаконечных множеств, которые в общем случае могутпересекатьсядруг с другом.

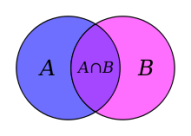
Случай двух множеств

Например, в случае двух множествA,B формула включений-исключений имеет вид:|AUB|=|A|+|B|-|A∩B|.

В сумме |A|+|B| элементы пересеченияA∩B учтены дважды, и чтобы компенсировать это мы вычитаем |A∩B| из правой части формулы. Справедливость этого рассуждения видна из диаграммы Эйлера-Веннадля двух множеств, приведенной на рисунке справа.

Таким же образом и в случае n>2 множеств процесс нахождения количества элементов объединенияA₁UA₂U…UA_n состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.

Для случая с большим количеством рассматриваемых множеств процесс нахождения количества элементов объединения состоит в поочередном включений ошибочно исключенного и исключений ошибочно включенного. Отсюда и происходит название формулы.

Впервые формулу включений-исключений опубликовал португальский математик Даниэль да Сильвав 1854 году Но еще в 1713 годуНиколай Бернулли. использовал этот метод для решения задачи Монмора, известной какзадача о встречах, частным случаем которой являетсязадача о беспорядках. Также формулу включений-исключений связывают с именами французского математикаАбрахама де Муавраи английского математикаДжозефа Сильвестра. В теории вероятностей аналог принципа включений-исключений известен как формула Пуанкаре

Билет 5

(Декартово произведение множеств и метод включений для доказательства равенств «сложных» множеств посредством применения операци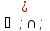й и.)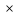

Декартово произведение множеств. Соответствия и способы их задания

Декартовым произведением двух множеств называется множество пар элементов, у которых первая компонента принадлежит первому множеству, вторая – второму.

Для множеств: A=(1;2;3) и B=(n;m декартово произведение имеет вид

D=AxB={(1;n), (1;m), (2;n), (2;m), (3;n), (3;m)}

Число элементов декартового произведения, равно произведению мощностей  данных множеств. n(AxB)=n(A)·n(B)

Декартово произведение задается периселением элементов, таблицей, координатной плоскостью и иными, понятными  способами.

AxB	n	m
1	(1;n)	(1;m)
2	(2;n)	(2;m)
3	(3;n)	(3;m)

Определение  декартового произведения двух множеств по  аналогии распространяется на любое число множеств, в том числе и на равные множества

Декартовым произведением n множеств называется множество кортежей длины n, у которых первая компонента принадлежит первому множеству, вторая – второму, …, компонента n принадлежит множеству n. Число элементов декартового  произведения n множеств равна произведению численностей всех множеств.

ЕслиА₁=А₂ =…=А_n =A, тоАⁿ =A x A x A x … x A.

Соответствием между двумя множествами является  любое подмножество декартового произведения этих множеств.

Соответствием между двумя множествами называется  правило, по которому каждому элементу множества X  выбирается элемент из множества Y.

Если рассматривать все  пары декартового произведения, то пара (a_i;b_j) задает  соответствие между элементами множества A={a₁; a₂; a₃;… a_n}  и множества B ={b₁; b₂; b₃;… b_m}.с соответствующими областями определения и значения.

Соответствие задается всеми способами, которыми задается декартово произведение двух множеств. Если соответствие задается  на координатной плоскости,  то область определения соответствия указывается на оси абсцисс, множество значений – оси ординат.

Если во всех парах, задающих соответствие R, компоненты поменять местами,  то получится соответствие R^-1, обратное данному соответствию.

Билет 6

(Операция взятия подмножеств непустого множества. Число всех подмножеств конечного п-элементного множества.)

Пусть —множество. Множество всех подмножеств множества называетсябулеаном (также степенью множества, показательным множеством или множеством частей) и обозначаетсяили. Ясно, чтои.

Число подмножеств конечного множества, состоящего из элементов равно .

Билет 7

(Соответствия и способы их задания посредством таблиц, графов, сечений, матриц. Примеры.)

(В теттр)

Билет 8

(Отображения. Области определения и значений отображения. Виды отображений.)

Пусть заданы два множества X и Y . Правило f, по которому каж-

дому элементу множества X сопоставляется однозначно определённый

элемент множества Y , принято называть функцией или отображением

из множества X в множество Y (обозначение f : X → Y ).

Тот факт, что элемент y множества Y является образом элемента x

множества X при отображении f, можно записать разными способами:

f(x) = y, xf = y, x^f = y.

Вернёмся к определению отображения. Оно требует, чтобы каждый

элемент x множества X имел образ y = xf в Y . Обратное верно не

всегда: могут существовать элементы множества Y , которые не имеют

прообразов в X. Те отображения

Отображение f : X → Y называется отображением множества X на множество Y или сюръекцией, если для каждого элемента y ∈ Y существует элемент x ∈ X такой, что y = xf. Соответствующее обозначение: f : X –(на)→Y .

Отображение f : X → Y называется взаимно

однозначным отображением из множества X в множество Y или инъ-

екцией, если для любых элементов x1, x2 ∈ X из равенства x1f = x2f

следует равенство x1 = x2. Соответствующее обозначение: f : X

−(1-1)→ Y

Отображение f : X → Y называется вза-

имно однозначным отображением множества X на множество Y или

биекцией, если оно является сюръекцией и инъекцией одновременно.

Соответствующее обозначение: f : X

−(1-1)(внизу на)→ Y

Отображение из множествав множествосчитается заданным, если каждому элементусопоставлен единственный элемент. Отображениеиз множествав множествообозначают записьюили. Элемент, который отображениемсопоставляется элементу, называют образом элементапри отображениии обозначают.

Каждое отображение однозначно определяет множество упорядоченных пар , являющееся подмножеством декартова произведениямножествана множествои называемое графиком отображения.

Понятие отображения можно обобщить. Обобщение может проходить по двум позициям. Во-первых, можно отказаться от полной определенности отображения, полагая, что образ определен не для каждого элемента множества , а для некоторых элементов этого множества. Тогда придем к понятию частичного отображения. При этом подмножество всех элементов, для которых определен образ, называют областью определения данного частичного отображения.

Многие элементарные функции являются частичными отображениями множества всех действительных чисел в себя. Например, функцияесть частичное отображение с областью определения

Во-вторых, можно отказаться от однозначности отображения, полагая, что данному сопоставлен не один, а несколько образов (множество образов) в множестве. В этом случае говорят, что задано соответствие из множествав множество.

Примером могут служить обратные тригонометрические функции: скажем, "большой" арксинус, сопоставляющий каждому множество всех таких чисел, что, т.е. множество, являющееся прообразом элементапри отображении, определяемом графиком функции.

Билет 9

(Понятие мощности множеств. Доказать, что множество всех подмножеств множества натуральных чисел несчетно.)

Мощность множества — это обобщение понятия количества (числа элементов множества), которое имеет смысл для всех множеств, включая бесконечные. Существуют бо́льшие, есть ме́ньшие бесконечные множества, среди них счётное множество является самым маленьким.

Мощность множества, как и другие основные конструкции традиционной теоретико-множественной математики, может достаточно плодотворно рассматриваться и под углом зрения, отличным от широко известной интуиционистской критики в рамках альтернативной теории множеств.

Пусть даны два множества иТогда они называются равномощными, если между нимисуществуетбиекция . Из свойств биекции следует, что равномощность являетсяотношением эквивалентности.Мощностью или кардинальным числом множества называется соответствующий емукласс эквивалентности. Мощность множества обозначается . Тот факт, что два множества равномощны, записывается:

Билет 10

В тетр

Билет 11

(Бинарные отношения и их свойства. Способы задания бинарных отношений. Примеры.)

Бинарным отношением между двумя множествами называется соответствие элементов одного из них элементам второго.

Пусть даны двамножестваи, и пусть-подмножествоихдекартова произведения. Тогда тройканазывается бинарным отношением междуиУтверждениеобычно записывается в видеи читается "соотносится с" Еслито пишутили

Бинарное отношение называется

-инъективным, если

-полным слева, если

-сюръективным (или полным справа), если

-функциональным, если

-функцией, если оно полно слева и функционально;

-биективным, если оно полно слева и справа, а также инъективно и функционально.

Виды отношений :

Рефлексивное симметричное транзитивное отношение называется отношением эквивалентности.

Рефлексивное антисимметричное транзитивное отношение называется отношением (частичного) порядка.

Бинарное отношениенамножественазывается отношением частичного порядка[1], если оно удовлетворяет свойствам

-рефлексивности: для всех ;

-антисимметричности: для всех ;

-транзитивности: для всех .

Билет 12

(Отношение эквивалентности на множестве М и разбиение множества М. Предложение 1. Примеры.)

Отношение эквивалентности - это обобщение понятия равенства. Эквивалентные элементы не различимы для теории в каком-то фиксированном смысле.

Определение

Бинарное отношение Р заданное на множестве  называется отношением эквивалентности, если оно

рефлексивно, то есть

симметрично, то есть

транзитивно, то есть

Предложение 1

Пусть Р отношение эквив-ти на мн-ве М. Тогда:

А) ає[а]_р, для любого аєМ(т.е любого элемента мно-ва М, принадл. классу который он пораждает )

Б) [a]_рᴖ[в]_р= ¢ или [а]_р=[в]_р для любых (а,в) є М.(т.е любые 2 класса или не пересек или совпадают)

В) [a]_р=[в]_р <=> аР*в (т.е классы эквив-и пораждает элем. И а и в совпад. тогда и только тогда, когда эти элем. наход-я в отнош Р)

Г) М= U[а]_р аєМ (т.е М-есть объед-е всех своих классов эквив-ти)

Разбие́ние мно́жества — это представление его в виде объединенияпроизвольного количества попарно непересекающихсяподмножеств.

Определение

Пусть суть произвольноемножество. Семействонепустыхмножеств, где индекспринимает значения в каком-то индекс-множестве (конечном или бесконечном), называется разбиением, если:

для любых , таких что;

.

Множества называются блоками разбиения множества.

Примеры:

--, где- множества всехцелых чисел,чётныхцелых чисел и нечётных целых чисел соответственно;

--Множество всех действительных чиселможет быть представлено в виде:.

Билет 13

(Порядковые отношения. Отношения частичного и линейного порядков. Отношение квазипорядка. Примеры.)

Пусть дано множство 

-Бинарное отношение наназывается предпорядком (или квазипорядком), если оно транзитивно и рефлексивно, то есть

1)

2)

-Бинарное отношение наназывается отношением нестрогого частичного порядка (или нестрогим порядком) на, если оно транзитивно, антисимметрично и рефлексивно, то есть

1)

2)

3)

-Бинарное отношение наназывается отношением строгого частичного порядка (или строгим порядком) на, если оно транзитивно и асимметрично, то есть

1)

2)

-Множество, на котором определён частичный порядок, называется частично упорядоченным.

-Отношение порядка , являющееся полным, то есть таким, что

называется полным порядком. Множество, на котором определён полный порядок, называется полностью упорядоченным (или цепью).

- Полное отношение в математике- это бинарное отношение, при котором любые два элемента соотносятся друг с другом некоторым образом.

Пусть на множествеопределенобинарное отношениеТогданазывается полным (или линейным), если

Билет 14 В тетр

(Наибольшие и наименьшие, максимальные и минимальные элементы частично упорядоченных множеств. Примеры.)

Линейно упорядоченное множество или цепь ― частично упорядоченное множество, в котором для любых двух элементовиимеет местоили.

Билет 15 В тетр

Билет 16

(Высказывания и логические операции над ними. Свойства логических операций. Базовая таблица истинности для логических операций.)

Логика высказываний (другое название — пропозициональная логика) — раздел логики, занимающийся изучением логических высказываний, операций над ними и их свойств.

Основные понятия

Базовыми понятиями логики высказываний являются пропозициональная переменная — переменная, значением которой может быть логическое высказывание, — и (пропозициональная) формула, определяемая индуктивноследующим образом:

1) Если P — пропозициональная переменная, то P — формула.

2) Если A — формула, то — формула.

3) Если A и B — формулы, то ,и— формулы.

4) Каждая формула может быть получена за конечное число шагов при помощи предыдущих трёх правил.

Знаки и(отрицание, конъюнкция, дизъюнкция и импликация) называются пропозициональными связками. Подформулой называется часть формулы, сама являющаяся формулой. Собственной подформулой называется подформула, не совпадающая со всей формулой.

Конъюнкция Дизъюнкция Материальная импликация

Равносильность Отрицание

Билет 17

(Индуктивный подход к построению множества всех формул алгебры высказываний посредством применения логических операций к исходным простым высказываниям . Сложность формулы. Примеры.)

Одним из наиболее методов определения объектов и совокупностей объектов назыв. метод индуктивных определений. Предположим, что нужно построить класс объектов К для этого:

1) Опред-ся исходные объекты, без всяких доп. обоснований. То есть непосредст. указ. те объекты( своеобраз атомы, которые нужно считать принадлежащим области К.

2) Указ-ся совокупность эффект-х правил которые позвол строить из ране построенных объектов строить все более и более слож объектов совокупности К

Построение совокупности К опред по шагам. Применим этот метод для построения совокуп К всех множеств которые можно получ из исход множеств(атомов) посредством приминения к ним теоретиком нож-ых операции.

А) базис индуктивного опред-я. Всякое исход мн-во А_і(і=1,2….) (вроде спит.) множеством строящихся совокуп-тей К. Всем этим множ-ам присвое-я сложность 0.

Б) индуктивное предполож.(шаг t). Предположим, что на шагах с номерами 0,1,2,…. t уже построены все множ-ва из класса К и определенны их сложности

В)Индукционный шаг(шаг t+1) множество шага t+1 строется исходя из мно-ва предшествующих шагов посредством прим к ним(не более раза) одной из теоретиком нож-х операций

При этом сложность множ М с шагом t+1 опред. По формуле S(M)=max[S(A);S(B)]+1, где А и В множество шагов 0,1,2,… t из которых получ мн-во М посредством прим-я теорет множ операции (т.е M=AᴗB; M=AᴖB; M= B\A)

Билет 18

(Отношение равносильности на множестве высказываний. Примеры. Основные равносильности (законы логики).)

Определение 4.1. Формулы иалгебры высказываний называютсяравносильными (эквивалентными), если при любых значениях входящих в них пропозициональных переменных логические значения получающихся из формул ивысказываний совпадают. Для указания равносильности формул используют обозначение. Определение равносильности формул можно записать символически для любых конкретных высказываний

Следствие 4.3. Отношение равносильности между формулами алгебры высказываний:

а) рефлексивно: ; б) симметрично: если , то; в) транзитивно: если и, то, т.е. отношение равносильности является отношением эквивалентности.

Билет 19

(Индуктивный подход к таблицам истинности данных формул алгебры высказываний и методы получения по данным таблицам истинности формул алгебры высказываний.)

Определение 2.1

1. Каждая отдельно взятая пропозициональная переменная есть формула алгебры высказываний.

2. Если и— формулы алгебры высказываний, то выражения также являются формулами алгебры высказываний:

3. Никаких других формул алгебры высказываний, кроме получающихся согласно пунктам 1 и 2, нет.

Определения такого типа называются индуктивными. В них имеются прямые пункты (в данном случае п. 1 и п. 2), где задаются объекты, которые в дальнейшем именуются определяемым термином (в данном случае — формулами алгебры высказываний), и косвенный пункт (в данном случае п. 3), в котором говорится, что такие объекты исчерпываются объектами, заданными в прямых пунктах. Среди прямых пунктов имеются базисные пункты (в данном случае п. 1), где указываются некоторые конкретные объекты, именуемые в дальнейшем определяемым термином, и индуктивные пункты (в данном случае п. 2), где даются правила получения определяемых объектов, в частности из объектов, перечисленных в базисных пунктах.

В данной лекции формулы алгебры высказываний будем называть просто формулами. Есть и другие названия для понятия формулы: правильно построенная формула или правильно построенное выражение, но они представляются менее предпочтительными. Само определение формулы, носящее индуктивный характер, на первых порах кажется непривычным. Определения такого типа вам ранее не встречались. Лучшее понимание этого определения наступит, когда вы научитесь применять его для определения того, является или не является формулой последовательность символов (слово), составленная из пропозициональных переменных, символов логических операций и скобок.

К этому полезно добавить следующее. Для каждой формулы должна существовать конечная последовательность всех ее подформул, т.е. такая конечная последовательность, которая начинается с входящих в данную формулу пропозициональных переменных, заканчивается самой этой формулой, и каждый член этой последовательности, не являющийся пропозициональной переменной, есть либо отрицание уже имеющегося члена этой последовательности, либо получается из двух уже имеющихся членов этой последовательности их соединением с помощью одного из знаков и заключением полученного выражения в скобки. Такую последовательность всех подформул данной формулы иногда называютпорождающей последовательностью для данной формулы. Наличие такой последовательности у логического выражения служит критерием того, что выражение является формулой. Это свойство отличает формулы.

Приведем примеры формул. На основании п. 1 определения 2.1 формулами будут пропозициональные переменные:

Далее на основании п. 2 того же определения из этих формул построим следующие:

Из построенных формул также на основании п. 2 строим еще более сложные формулы:

Ясно, что процесс построения все более сложных формул может продолжаться безгранично.

Приведем примеры выражений, не являющихся формулами. Это в каком-то смысле нелепые выражения. К примеру, выражение было бы формулой на основании п. 2 определения 2.1, если бы формулами были выраженияи. Выражениеесть пропозициональная переменная и потому на основании п. 1 определения 2.1 является формулой. Рассмотрим выражение. Оно было бы формулой, если бы между формуламиистоял один из знаков логических связок. Но такого знака нет. Следовательно, выражениене формула, и исходное выражениеформулой также не является.

Таким образом, индуктивный характер определения 2.1 дает возможность эффективно решать для каждого выражения, является оно формулой алгебры высказываний или нет.

Билет 20

(Релейно-контактные схемы. Методы перехода от Р.К.С. к приведенным формулам и от приведенных формул к Р.К.С. Методы упрощения Р.К.С.)

Релейно-контактная схема представляет собой устройство из проводников и контактов, связывающих полюса источника тока. Контакты могут быть размыкающими и замыкающими. Каждый контакт подключен к некоторому реле. Когда реле находится под током, все подключенные к нему замыкающие контакты замкнуты, а размыкающие - разомкнуты.

         Каждому реле можно поставить в соответствие значение 1, если оно находится под током, и 0, если нет. Все замыкающие контакты, подключенные к реле х, будем обозначать x₁, ... x_n, а размыкающие - .

  Всей схеме также можно поставить одно из двух значений 1, если схема проводит ток, и 0, если не проводит. Это значение есть функция переменных х_i, , т.е. логическая функция. Эту функцию называют функцией проводимости электрической цепи.

         Всякая формула алгебры высказываний может быть реализована некоторой релейно-контактной схемой, имеющей соответствующую функцию проводимости. И наоборот, для некоторой схемы можно указать ее функцию проводимости, логическую функцию, а затем построить для нее некоторую формулу алгебры высказываний. При этом основные логические связки моделируются следующими элементарными схемами:

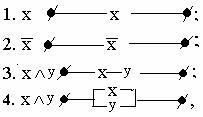
т.е. дизъюнкция моделируется параллельным соединением проводников, конъюнкция - последовательным.

 Можно установ такое соотв м\у приведенными формулами и рел контактными схемами при которых формулыбудут приним значения истины тога когда соотв РКС будет пропуск электр ток.

Упрощается методом склеивания.

Билет 21

(Построение Р.К.С. по заданным условиям. Пример на решение задачи о перевозе.)

Релейно-контактная схема представляет собой устройство из проводников и контактов, связывающих полюса источника тока. Контакты могут быть размыкающими и замыкающими. Каждый контакт подключен к некоторому реле. Когда реле находится под током, все подключенные к нему замыкающие контакты замкнуты, а размыкающие - разомкнуты.

         Каждому реле можно поставить в соответствие значение 1, если оно находится под током, и 0, если нет. Все замыкающие контакты, подключенные к реле х, будем обозначать x₁, ... x_n, а размыкающие - .

  Всей схеме также можно поставить одно из двух значений 1, если схема проводит ток, и 0, если не проводит. Это значение есть функция переменных х_i, , т.е. логическая функция. Эту функцию называют функцией проводимости электрической цепи.

         Всякая формула алгебры высказываний может быть реализована некоторой релейно-контактной схемой, имеющей соответствующую функцию проводимости. И наоборот, для некоторой схемы можно указать ее функцию проводимости, логическую функцию, а затем построить для нее некоторую формулу алгебры высказываний. При этом основные логические связки моделируются следующими элементарными схемами:

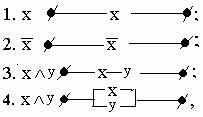
т.е. дизъюнкция моделируется параллельным соединением проводников, конъюнкция - последовательным.

 Можно установ такое соотв м\у приведенными формулами и рел контактными схемами при которых формулыбудут приним значения истины тога когда соотв РКС будет пропуск электр ток.

Упрощается методом склеивания.

Билет 22

(Общая схема построения формальной аксиоматической теории и реализация этой схемы применительно к построению исчисления высказываний.)

Формальные аксиоматические теории. Аксиомы и правила вывода И.В.

Аксиомы:

A1:A→(B→A)

A2:((A→(B→C))→((A→B)→(A→C)))

A3: ((A&B)→A)

A4: ((A&B)→B)

A5: ((A→B) →((A→C) →(A→(B&C))))

A6: ((A→(A ˅ B))

A7: ((B→(A˅B))

A8: ((A→C) →((B→C) →((A ˅B) →C)))

A9: A→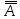

A10: 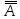→A

A11: ((A→B) →())

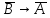Правило вывода:

A→B,A

B

Билет 23

(Аксиомы и правила вывода И.В. Понятие доказательства (вывода) и теоремы в И.В. Примеры выводов и выводимых формул.)

Формальные аксиоматические теории. Аксиомы и правила вывода И.В.

Аксиомы:

A1:A→(B→A)

A2:((A→(B→C))→((A→B)→(A→C)))

A3: ((A&B)→A)

A4: ((A&B)→B)

A5: ((A→B) →((A→C) →(A→(B&C))))

A6: ((A→(A ˅ B))

A7: ((B→(A˅B))

A8: ((A→C) →((B→C) →((A ˅B) →C)))

A9: A→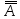

A10: 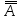→A

A11: ((A→B) →())

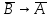Правило вывода:

A→B,A

B

Понятие вывода (доказательства) в исчислении высказываний. Теоремы И.В. Примеры.

Понятие вывода должно быть эффективным. Иными словами, должна иметься эффективная процедура, позволяющая для произвольной конечной последовательности формул решить, может ли каждый член этой последовательности быть выведен из одной или нескольких предшествующих формул этой последовательности посредствам некоторых фиксированных правил вывода.

В такой формальной аксиоматической теории оказывается эффективным и понятие доказательства; иными словами, в такой теории имеется эффективная процедура, позволяющая для произвольной конечной последовательности формул решить, является ли она доказательством.

Теорема о дедукции: если Г, В ├ А, то Г ├ В → А, где Г - это набор некоторых формул Г={F₁, F₂, ..., F_n}.

Следствие: тогда и только тогда F₁, F₂, ..., F_n ├ A, когда ├F₁→(F₂→...→(F_n-1→(F_n→A))...)

Доказательство: пусть F₁, F₂, ..., F_n ├ A. Тогда, применяя теорему о дедукции, имеем F₁, F₂, ..., F_n-1 ├ F_n→A.

Аналогично F₁,F₂,...,F_n-2├F_n-1→(F_n→A), и т.д. Продолжая этот процесс необходимое число раз, получаем ├F₁→(F₂→...→(F_n-1→(F_n→A))...)

Для доказательства достаточности предположим, что ├B, где B=F₁→(F₂→...→(F_n-1→(F_n→A))...). По правилу заключения получаем F₁├(F₂→...→(F_n-1→(F_n→A))...). Далее, через n шагов имеем F₁,F₂,...,F_n├A.

Таким образом, благодаря следствию, проверка выводимости формулы A из формул F₁,F₂,...,F_n, сводится к проверке доказуемости формулы F₁→(F₂→...→(F_n-1→(F_n→A))...).

Формула A называется тождественно истинной (или тавтологией), если значение формулы A равно единице при любых наборах значений пропозициональных переменных. Следующая теорема сводит проверку доказуемости формулы к проверке ее тождественной истинности.

Теорема о полноте. Формула A доказуема тогда и только тогда, когда A тождественно истинна т(автология): ├A⇔A - тавтология.

Таким образом, для того чтобы установить, доказуема ли формула, достаточно составить ее таблицу истинности. Как известно, существует эффективный алгоритм построения таблицы истинности, и, значит, ИВ разрешимо.

Пример. Докажем, что P├P. По теореме о дедукции это равносильно тому, что ├(Р→Р). В свою очередь, по теореме о полноте, достаточно доказать, что (Р→Р) тавтология. Составляя таблицу истинности для формулы (Р→Р), убеждаемся, что (Р→Р) тождественно истинна и, следовательно, доказуема.

Теорема о непротиворечивости. Исчисление ИВ непротиворечиво.

Доказательство. По теореме о полноте любая формула, не являющаяся тождественно истинной, не доказуема в ИВ. Например, такой формулой является формула А∧(¬А).

Множество формул Г называется противоречивым, если Г├А∧(¬А). Если Г — противоречивое множество формул, будем обозначать этот факт через Г├.

Утверждение. Формула А выводима из множества формул Г тогда и только тогда, когда множество Г∩{¬A} — противоречиво.

 

Билет 24

(Дизъюнктивные и конъюнктивные нормальные формы и алгоритмы приведения к ним. Примеры. Истинностные характеризации Д.Н.Ф. и К.Н.Ф.)

Дизъюнктивная нормальная форма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любаябулева формула может быть приведена к ДНФ.Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем

Дизъюнктивные нормальные формы и алгоритмы приведения к ним

Дизъюнкция конечного множества элементарных конъюнкций называется дизъюнктивной нормальной формой(ДНФ). Число элементарных конъюнкций, образующих дизъюнктивную нормальную форму(ДНФ) называется длиной ДНФ. ДНФ содержащая только полные элементарные конъюнкции называется совершенной ДНФ(или СДНФ). Любую логическую формулу А можно представить в виде ДНФ, а затем ДНФ в виде СДНФ.

Алгоритм построения СДНФ:

Легко построить СДНФ, представляющую произвольную булеву функцию, заданную в табличной форме. Для этого достаточно выделить наборы (σ₁,σ₂,…,σ_n) , на которых функция принимает значение 1, и для каждого из них ввести в СДНФ полную элементарную конъюнкцию, где любая переменная X_i присутствует с отрицанием, если σ_i=0, и без отрицания, если σ_i=1.

Очевидно, для любой булевой функции f(x₁,x₂,…,x_n), кроме константы 0, существует единственная СДНФ (с точностью до порядка литералов и конъюнкций). Поэтому данная форма представления булевой функции является канонической